python实现傅里叶级数展开的实现

傅立叶级数的介绍我就不说了，自己也是应用为主，之前一直觉得很难懂，但最近通过自己编程实现了一些函数的傅立叶级数展开之后对傅立叶 级数展开的概念比较清楚了

(1)函数如下

函数图象如下：

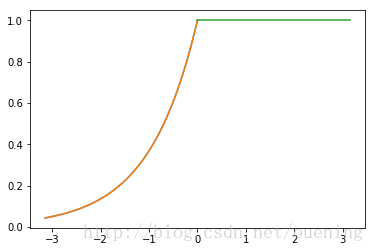
代码：

from pylab import *
x = mgrid[-10:10:0.02] # 这里类似于MATLAB用冒号产生步长为0.02的序列，但是语法和MATLAB不同
n = arange(1,1000)
def fourier_transform():
 a0 = (1-exp(-pi))/pi+1
 s=a0/2
 for i in range(1,100,1):
 s0 = ( (1-(-1)**i*exp(-pi))/(pi*(1+i**2))*cos(i*x)+1/pi*( (-i*(1-(-1)**i*exp(-pi)))/(1+i**2) + (1-(-1)**i)/i ) * sin(i*x) )
 s=s+s0
 plot(x,s,'orange',linewidth=0.6)
 title('fourier_transform')
 show() 

fourier_transform()

结果如下：

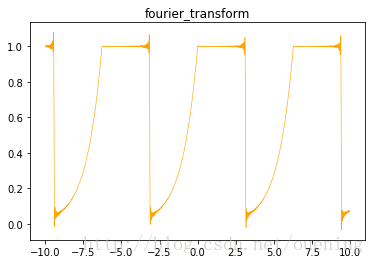
（2）

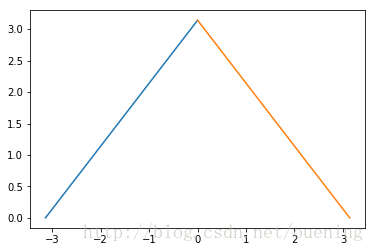
转换代码：

from pylab import *
def fourier1():
 s=pi/2

 for i in range(1,100,1):
 s0 = 2/pi*(1-(-1)**i)/i**2 * cos(i*x)
 s=s+s0
 plot(x,s,'orange',linewidth=0.6)
 title('fourier1')
 show()
fourier1()

结果如下：

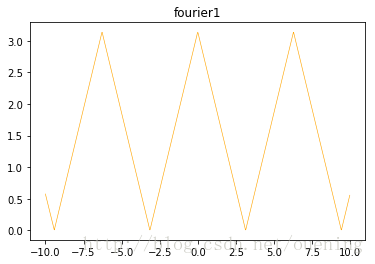
关于傅里叶级数展开的还有一些例子在我的另一篇博客https://www.jb51.net/article/144196.htm也有讨论，通过以上的例子可以很好直观感受傅立叶级数的作用，在电气工程上对分析流经变压器的谐波分量、整流装置输出谐波等分析具有重要作用。

还有一点就是python的强大功能，利用for循环语句可以方便地实现级数展开的求和运算，自己感觉编程起来比MATLAB/Octave跟快

相关文章：Python实现快速傅里叶变换（FFT）

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持我们。

赞 (0)

相关推荐

  • Python实现快速傅里叶变换的方法（FFT）

    本文介绍了Python实现快速傅里叶变换的方法(FFT),分享给大家,具体如下: 这里做一下记录,关于FFT就不做介绍了,直接贴上代码,有详细注释的了: import numpy as np from scipy.fftpack import fft,ifft import matplotlib.pyplot as plt import seaborn #采样点选择1400个,因为设置的信号频率分量最高为600赫兹,根据采样定理知采样频率要大于信号频率2倍,所以这里设置采样频率为1400赫兹(即

  • FFT快速傅里叶变换的python实现过程解析

    FFT快速傅里叶变换的python实现过程解析

    FFT是DFT的高效算法,能够将时域信号转化到频域上,下面记录下一段用python实现的FFT代码. # encoding=utf-8 import numpy as np import pylab as pl # 导入和matplotlib同时安装的作图库pylab sampling_rate = 8000 # 采样频率8000Hz fft_size = 512 # 采样点512,就是说以8000Hz的速度采512个点,我们获得的数据只有这512个点的对应时刻和此时的信号值. t = np.l

  • Python中的id()函数指的什么

    Python官方文档给出的解释是 id(object) Return the "identity" of an object. This is an integer (or long integer) which is guaranteed to be unique and constant for this object during its lifetime. Two objects with non-overlapping lifetimes may have the same

  • opencv python 傅里叶变换的使用

    理论 傅立叶变换用于分析各种滤波器的频率特性,对于图像,2D离散傅里叶变换(DFT)用于找到频域.快速傅里叶变换(FFT)的快速算法用于计算DFT. 于一个正弦信号,x(t)=Asin(2πft),我们可以说 f 是信号的频率,如果它的频率域被接受,我们可以看到 f 的峰值.如果信号被采样来形成一个离散信号,我们得到相同的频率域,但是在[−π,π] or [0,2π]范围内是周期性的 (or [0,N] for N-point DFT). 可以将图像视为在两个方向上采样的信号.因此,在X和Y方向

  • 使用python实现离散时间傅里叶变换的方法

    使用python实现离散时间傅里叶变换的方法

    我们经常使用傅里叶变换来计算数字信号的频谱,进而分析数字信号,离散时间傅里叶变换的公式为: 可是自己动手实现一遍才是最好的学习. 在数字分析里面,傅里叶变换默认等时间间隔采样,不需要时间序列,只需要信号数组即可分析. 分析过程如下: 对于含有 n 个样本值的数字信号序列,根据奈奎斯特采样定律,包含的周期数最大为 n/2,周期数为 0 代表直流分量.所以,当周期数表示为离散的 0,1,2,3-n/2 ,总的数目为 n/2+1个 傅里叶变换之后的结果为复数, 下标为 k 的复数 a+b*j 表示时域

  • python傅里叶变换FFT绘制频谱图

    本文实例为大家分享了python傅里叶变换FFT绘制频谱图的具体代码,供大家参考,具体内容如下 频谱图的横轴表示的是 频率, 纵轴表示的是振幅 #coding=gbk import numpy as np import pandas as pd import matplotlib.pyplot as plt #依据快速傅里叶算法得到信号的频域 def test_fft(): sampling_rate = 8000 #采样率 fft_size = 8000 #FFT长度 t = np.arang

  • python连接数据库的方法

    python连接数据库的方法

    MYSQL模块暂时还不支持python3.0以上的版本,由于我下载的python是3.0版本的,所以想要连接数据库只能利用其它的方法. Python3.x连接MySQL的方案有:oursql, PyMySQL, myconnpy 等,这里主要是安装pymysql 1.安装 pymysql安装:找到python文件夹pip程序的位置打开命令窗口: pip install pymysql3 2.使用 安装完毕后,数据库连接的具体步骤如下 引入 API 模块. 获取与数据库的连接. 执行SQL语句和存

  • python实现傅里叶级数展开的实现

    python实现傅里叶级数展开的实现

    傅立叶级数的介绍我就不说了,自己也是应用为主,之前一直觉得很难懂,但最近通过自己编程实现了一些函数的傅立叶级数展开之后对傅立叶 级数展开的概念比较清楚了 (1)函数如下 函数图象如下: 代码: from pylab import * x = mgrid[-10:10:0.02] # 这里类似于MATLAB用冒号产生步长为0.02的序列,但是语法和MATLAB不同 n = arange(1,1000) def fourier_transform(): a0 = (1-exp(-pi))/pi+1

  • Python模块汇总(常用第三方库)

    模块 定义 计算机在开发过程中,代码越写越多,也就越难以维护,所以为了编写可维护的代码,我们会把函数进行分组,放在不同的文件里.在python里,一个.py文件就是一个模块 优点: 提高代码的可维护性. 提高代码的复用,当模块完成时就可以在其他代码中调用 引用其他模块,包含python内置模块和其他第三方模块 避免函数名和变量名等名称冲突 Python语言生态 Python语言提供超过15万个第三方库,Python库之间广泛联系.逐层封装. 使用pip安装 Python社区:https://py

  • python实现周期方波信号频谱图

    在学习傅里叶变换的时候遇到了求周期方波信号频谱图的例子,在书上和网上查阅了一些资料,发现大都是讨论的都是下图左边的周期信号的频谱,课程老师的PPT中也只列出了另一种周期信号频谱图的结论,没有在进行傅里叶变换,自己便根据定义推导了一遍,贴在这里作记录和分享之用. 关于傅立叶级数展开的另一讨论在我的另一篇文章https://www.jb51.net/article/144194.htm 2016年11月21号更新 在第二个周期方波信号的傅里叶变换里,注意是 转换为sin函数下为 之前写错了,今天更正

  • python实现逆滤波与维纳滤波示例

    构建运动模糊模型 现假定相机不动,图像f(x,y)在图像面上移动并且图像f(x,y)除移动外不随时间变化.令x0(t)和y0(t)分别代表位移的x分量和y分量,那么在快门开启的时间T内,胶片上某点的总曝光量是图像在移动过程中一系列相应像素的亮度对该点作用之总和.也就是说,运动模糊图像是由同一图像在产生距离延迟后与原图像想叠加而成.如果快门开启与关闭的时间忽略不计,则有: 由于各种运动都是匀速直线运动的叠加,因而我们只需考虑匀速直线运动即可.但由于我们自身水平有限,且旨在探讨找到实现运动模糊复原方

  • 如何利用python进行时间序列分析

    题记:毕业一年多天天coding,好久没写paper了.在这动荡的日子里,也希望写点东西让自己静一静.恰好前段时间用python做了一点时间序列方面的东西,有一丁点心得体会想和大家分享下.在此也要特别感谢顾志耐和散沙,让我喜欢上了python. 什么是时间序列 时间序列简单的说就是各时间点上形成的数值序列,时间序列分析就是通过观察历史数据预测未来的值.在这里需要强调一点的是,时间序列分析并不是关于时间的回归,它主要是研究自身的变化规律的(这里不考虑含外生变量的时间序列). 为什么用python

  • python数字图像处理之估计噪声参数

    python数字图像处理之估计噪声参数

    估计噪声参数 周期噪声的参数通常是通过检测图像的傅里叶谱来估计的. 只能使用由传感器生成的图像时,可由一小片恒定的背景灰度来估计PDF的参数. 来自图像条带的数据的最简单用途是,计算灰度级的均值和方差.考虑由 S S S表示的一个条带(子图像),并令 P S ( z i ) P_{S}(z_i) PS​(zi​), i = 0 , 1 , 2 , - , L − 1 i = 0, 1, 2, \dots, L-1 i=0,1,2,-,L−1表示 S S S中的像素灰度的概率估计(归一化直方图值)

  • Python 中的Sympy详细使用

    Python 中的Sympy详细使用

    遇到复杂计算找python绝对不让你失望,sympy是一个Python的科学计算库,用一套强大的符号计算体系完成诸如多项式求值.求极限.解方程.求积分.微分方程.级数展开.矩阵运算等等计算问题.虽然Matlab的类似科学计算能力也很强大,但是Python以其语法简单.易上手.异常丰富的三方库生态,个人认为可以更优雅地解决日常遇到的各种计算问题.安装在本博客就不细讲了!  1.表达式与表达式求值: #--------多项式求解-------- #定义变量 x=sympy.Symbol('x') f

  • Python与Matlab实现快速傅里叶变化的区别

    Python与Matlab实现快速傅里叶变化的区别

    注:两种语言的fft算法是有区别的,最后细聊! Matlab的fftlw函数 输入是信号序列.对应的时间序列.以及是否作图,输出可以得到单边归一化之后的频率与对应的振幅,通过输出可以直接画出常用的频谱图! function [ F,M ] = fftlw( x,y,draw ) %FFTLW 快速傅里叶变化2021.10.26 %输入 x--时间 y--信号 draw--1为画频谱图,0为不画 %输出 F--频率 M--幅值 N=length(y); %采样点数 if(mod(N,2)>0) N

  • 基于Python实现图像的傅里叶变换

    基于Python实现图像的傅里叶变换

    目录 前言 (1)基本概念 (2)读取图像信息 1. 傅里叶变换 (1)基本概念 (2)numpy实现 (3)OpevCV实现  2. 傅里叶逆变换 (1)基本概念 (2)代码实现 前言 首先是本文总体代码,改一下图像的读取路径就可以运行了,但我还是建议大家先看后面的步骤一行行敲代码,这样效果更好: """ Author:XiaoMa date:2021/11/7 """ import cv2 import matplotlib.pyplot a

随机推荐