PyTorch搭建一维线性回归模型（二）

PyTorch基础入门二：PyTorch搭建一维线性回归模型

1）一维线性回归模型的理论基础

给定数据集，线性回归希望能够优化出一个好的函数，使得能够和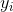尽可能接近。

如何才能学习到参数和呢？很简单，只需要确定如何衡量与之间的差别，我们一般通过损失函数（Loss Funciton)来衡量：。取平方是因为距离有正有负，我们于是将它们变为全是正的。这就是著名的均方误差。我们要做的事情就是希望能够找到和，使得：

均方差误差非常直观，也有着很好的几何意义，对应了常用的欧式距离。现在要求解这个连续函数的最小值，我们很自然想到的方法就是求它的偏导数，让它的偏导数等于0来估计它的参数，即：

求解以上两式，我们就可以得到最优解。

2）代码实现

首先，我们需要“制造”出一些数据集：

import torch
import matplotlib.pyplot as plt

x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1)
y = 3*x + 10 + torch.rand(x.size())
# 上面这行代码是制造出接近y=3x+10的数据集，后面加上torch.rand()函数制造噪音

# 画图
plt.scatter(x.data.numpy(), y.data.numpy())
plt.show()

我们想要拟合的一维回归模型是。上面制造的数据集也是比较接近这个模型的，但是为了达到学习效果，人为地加上了torch.rand()值增加一些干扰。

上面人为制造出来的数据集的分布如下：

有了数据，我们就要开始定义我们的模型，这里定义的是一个输入层和输出层都只有一维的模型，并且使用了“先判断后使用”的基本结构来合理使用GPU加速。

class LinearRegression(nn.Module):
  def __init__(self):
    super(LinearRegression, self).__init__()
    self.linear = nn.Linear(1, 1) # 输入和输出的维度都是1
  def forward(self, x):
    out = self.linear(x)
    return out

if torch.cuda.is_available():
  model = LinearRegression().cuda()
else:
  model = LinearRegression()

然后我们定义出损失函数和优化函数，这里使用均方误差作为损失函数，使用梯度下降进行优化：

criterion = nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=1e-2)

接下来，开始进行模型的训练。

num_epochs = 1000
for epoch in range(num_epochs):
  if torch.cuda.is_available():
    inputs = Variable(x).cuda()
    target = Variable(y).cuda()
  else:
    inputs = Variable(x)
    target = Variable(y)

  # 向前传播
  out = model(inputs)
  loss = criterion(out, target)

  # 向后传播
  optimizer.zero_grad() # 注意每次迭代都需要清零
  loss.backward()
  optimizer.step()

  if (epoch+1) %20 == 0:
    print('Epoch[{}/{}], loss:{:.6f}'.format(epoch+1, num_epochs, loss.data[0]))

首先定义了迭代的次数，这里为1000次，先向前传播计算出损失函数，然后向后传播计算梯度，这里需要注意的是，每次计算梯度前都要记得将梯度归零，不然梯度会累加到一起造成结果不收敛。为了便于看到结果，每隔一段时间输出当前的迭代轮数和损失函数。

接下来，我们通过model.eval()函数将模型变为测试模式，然后将数据放入模型中进行预测。最后，通过画图工具matplotlib看一下我们拟合的结果，代码如下：

model.eval()
if torch.cuda.is_available():
  predict = model(Variable(x).cuda())
  predict = predict.data.cpu().numpy()
else:
  predict = model(Variable(x))
  predict = predict.data.numpy()
plt.plot(x.numpy(), y.numpy(), 'ro', label='Original Data')
plt.plot(x.numpy(), predict, label='Fitting Line')
plt.show()

其拟合结果如下图：

附上完整代码：

# !/usr/bin/python
# coding: utf8
# @Time  : 2018-07-28 18:40
# @Author : Liam
# @Email  : luyu.real@qq.com
# @Software: PyCharm
#            .::::.
#           .::::::::.
#           :::::::::::
#         ..:::::::::::'
#        '::::::::::::'
#         .::::::::::
#      '::::::::::::::..
#         ..::::::::::::.
#        ``::::::::::::::::
#        ::::``:::::::::'    .:::.
#        ::::'  ':::::'    .::::::::.
#       .::::'   ::::   .:::::::'::::.
#      .:::'    ::::: .:::::::::' ':::::.
#      .::'    :::::.:::::::::'   ':::::.
#     .::'     ::::::::::::::'     ``::::.
#   ...:::      ::::::::::::'       ``::.
#   ```` ':.     ':::::::::'         ::::..
#            '.:::::'          ':'````..
#           美女保佑 永无BUG

import torch
from torch.autograd import Variable
import numpy as np
import random
import matplotlib.pyplot as plt
from torch import nn

x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1)
y = 3*x + 10 + torch.rand(x.size())
# 上面这行代码是制造出接近y=3x+10的数据集，后面加上torch.rand()函数制造噪音

# 画图
# plt.scatter(x.data.numpy(), y.data.numpy())
# plt.show()
class LinearRegression(nn.Module):
  def __init__(self):
    super(LinearRegression, self).__init__()
    self.linear = nn.Linear(1, 1) # 输入和输出的维度都是1
  def forward(self, x):
    out = self.linear(x)
    return out

if torch.cuda.is_available():
  model = LinearRegression().cuda()
else:
  model = LinearRegression()

criterion = nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=1e-2)

num_epochs = 1000
for epoch in range(num_epochs):
  if torch.cuda.is_available():
    inputs = Variable(x).cuda()
    target = Variable(y).cuda()
  else:
    inputs = Variable(x)
    target = Variable(y)

  # 向前传播
  out = model(inputs)
  loss = criterion(out, target)

  # 向后传播
  optimizer.zero_grad() # 注意每次迭代都需要清零
  loss.backward()
  optimizer.step()

  if (epoch+1) %20 == 0:
    print('Epoch[{}/{}], loss:{:.6f}'.format(epoch+1, num_epochs, loss.data[0]))
model.eval()
if torch.cuda.is_available():
  predict = model(Variable(x).cuda())
  predict = predict.data.cpu().numpy()
else:
  predict = model(Variable(x))
  predict = predict.data.numpy()
plt.plot(x.numpy(), y.numpy(), 'ro', label='Original Data')
plt.plot(x.numpy(), predict, label='Fitting Line')
plt.show()

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持我们。