数据结构简明备忘录 线性表

线性表

线性表是线性结构的抽象，线性结构的特点是结构中的数据元素之间存在一对一的线性关系。
数据元素之间的位置关系是一个接一个的排列：
.除第一个位置的数据元素外，其他数据元素位置的前面都只有一个数据元素。
.除最后一个位置的外，其他数据元素位置的后面都只有一个元素。
线性表通常表示为：L=(D,R)
D是数据元素的有限集合
R是数据元素之间关系的有限集合

线性表的基本操作：


代码如下:

public interface IListDS<T> {
int GetLength(); //求长度
void Clear(); //清空
bool IsEmpty(); //判空
void Append(T item); //附加
void Insert(T item, int i); //插入
T Delete(int i); //删除
T GetElement(int i); //取表元素
int Locate(T value); //按值查找
}

顺序表

顺序表是线性表的顺序存储(Sequence Storage)，是指在内存中用一块地址连续的空间依次存放线性表的数据元素(Sequence List)，具有随机存取的特点。

w: 每个数据元素占w个存储单元
A1:顺序表的基地址(Base Address)
Loc(Ai)=Loc(A1)+(i-1)*w 1<=i<=n

为了理解顺序表，闪电学习了这样一个例题，有兴趣的朋友可以在自己的机器上写一下。
有数据类型为整型的顺序表La和Lb，其数据元素均按从小到大的升序排列，编写一个算法将它们合并成一个表Lc，要求Lc中数据元素也按升序排列。
算法思路：
依次扫描La和Lb的数据元素，比较La和Lb当前数据元素的值，将较小值的数据元素赋给Lc，如此直到一个顺序表被扫描完，然后将未完的那个顺序表中余下的数据元素赋给Lc即可。Lc的容量要能够容纳La和Lb两个表相加的长度。
思路图示：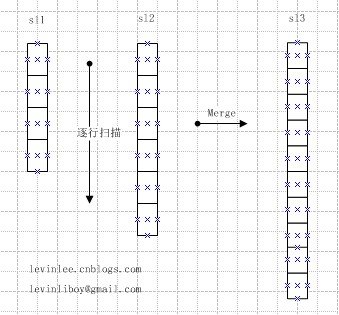



代码如下:

public class SeqList<T> : IListDS<T> {
private int maxsize; //顺序表的容量
private T[] data; //数组，用于存储顺序表中的数据元素
private int last; //指示顺序表最后一个元素的位置

//构造器
public SeqList(int size)
{
data = new T[size];
maxsize = size;
last = -1; //如果顺序表为空，last=-1
}
//索引器
public T this[int index]
{
get { return data[index]; }
set { data[index] = value; }
}
//最后一个元素的位置属性
public int Last
{
get { return last; }
}
//容量属性
public int Maxsize
{
get { return maxsize; }
set { maxsize = value; }
}
//判断顺序表是否为空
public bool IsEmpty()
{
if (last == -1)
return true;
else
return false;
}
//判断顺序表是否为满
public bool IsFull()
{
if (last == maxsize - 1)
return true;
else
return false;
}
//求顺序表的长度
public int GetLength()
{
return last + 1;
}
//清空顺序表
public void Clear()
{
last = -1;
}
//在顺序表末尾添加新元素
public void Append(T item)
{
if (IsFull())
{
Console.WriteLine("List is full.");
return;
}
data[++last] = item;
}

//在顺序表第i个数据元素位置插入一个数据元素
public void Insert(T item, int i)
{
if (IsFull())
return;
if (i < 1 || i > last + 2)
return;
if (i == last + 2)
data[last + 1] = item;
else
{
for (int j = last; j >= i - 1; --j)
{
data[j + 1] = data[j];
}
data[i - 1] = item;
}
++last;
}
//删除顺序表的第i个数据元素
public T Delete(int i)
{
T tmp = default(T);
if (IsEmpty())
return tmp;
if (i < 1 || i > last + 1)
return tmp;
if (i == last + 1)
tmp = data[last--];
else
{
tmp = data[i - 1];
for (int j = i; j <= last; ++j)
data[j] = data[j + 1];
}
--last;
return tmp;
}
//获得顺序表的第i个数据元素
public T GetElement(int i)
{
if (IsEmpty() || (i < 1) || (i > last + 1))
return default(T);
return data[i-1];
}
//在顺序表中查找值为value的数据元素
public int Locate(T value)
{
if (IsEmpty())
return -1;
int i = 0;
for (i = 0; i <= last; ++i)
{
if (value.Equals(data[i]))
break;
}
if (i > last)
return -1;
return i;
}
}

代码如下:

public class GenericList
{
public GenericList()
{ }
public SeqList<int> Merge(SeqList<int> La, SeqList<int> Lb)
{
SeqList<int> Lc = new SeqList<int>(La.Maxsize+Lb.Maxsize);
int i = 0;
int j = 0;
int k = 0;
//两个表中元素都不为空
while ((i <= (La.GetLength() - 1)) && (j <= (Lb.GetLength() - 1)))
{
if (La[i] < Lb[j])
Lc.Append(La[i++]);
else
Lc.Append(Lb[j++]);
}
//a表中还有数据元素
while (i <= (La.GetLength() - 1))
Lc.Append(La[i++]);
//b表中还有数据元素
while (j <= (Lb.GetLength() - 1))
Lc.Append(Lb[j++]);
return Lc;
}
}

客户端代码：


代码如下:

static void Main(string[] args)
{
SeqList<int> sl1 = new SeqList<int>(4);
sl1.Append(1);
sl1.Append(3);
sl1.Append(4);
sl1.Append(7);
SeqList<int> sl2 = new SeqList<int>(6);
sl2.Append(2);
sl2.Append(5);
sl2.Append(6);
sl2.Append(8);
sl2.Append(11);
sl2.Append(14);
GenericList gl = new GenericList();
SeqList<int> sl3 = gl.Merge(sl1, sl2);
Console.WriteLine("length:" + sl3.GetLength());
for (int i = 0; i < sl3.GetLength(); i++)
{
Console.WriteLine(i + ":" + sl3[i]);
}
}

好了，下一次学习链表。
作者：LevinLee