深入理解卡特兰数及其应用

Catalan number，卡特兰数又称卡塔兰数，是组合数学中一个常出现在各种计数问题中出现的数列。以比利时的数学家欧仁·查理·卡塔兰 (1814–1894)命名。

令h(0)=1,h(1)=1，catalan数满足递推式：h(n)= h(0)*h(n-1)+h(1)*h(n-2) + ... + h(n-1)h(0) (n>=2)

catalan数公式的一般是形式为：

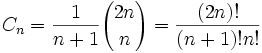
递推关系：


它也满足

 
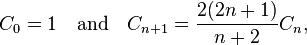
这提供了一个更快速的方法来计算卡塔兰数。

卡特兰数的应用n个元素顺序入栈，出栈顺序有多少种？此问题是一个卡特兰数问题，证明过程如下：

令1表示进栈，0表示出栈，则可转化为求一个2n位、含n个1、n个0的二进制数，满足从左往右扫描到任意一位时，经过的0数不多于1数。显然含n个1、n个0的2n位二进制数共有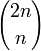个，下面考虑不满足要求的数目。

考虑一个含n个1、n个0的2n位二进制数，扫描到第2m+1位上时有m+1个0和m个1（容易证明一定存在这样的情况），则后面的0-1排列中必有n-m个1和n-m-1个0。将2m+2及其以后的部分0变成1、1变成0，则对应一个n+1个0和n-1个1的二进制数。

反过来，任何一个由n+1个0和n-1个1组成的2n位二进制数，由于0的个数多2个，2n为偶数，故必在某一个奇数位上出现0的累计数超过1的累计数。同样在后面部分0和1互换，使之成为由n个0和n个1组成的2n位数，即n+1个0和n-1个1组成的2n位数必对应一个不符合要求的数。
因而不合要求的2n位数与n+1个0，n－1个1组成的排列一一对应。 显然，不符合要求的方案数为c(2n,n+1)。

从而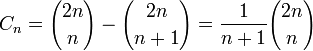。证毕。

括号化问题   如，矩阵链乘： P=a1×a2×a3×……×an，依据乘法结合律，不改变其顺序，只用括号表示成对的乘积，试问有几种括号化的方案？(h(n)种)

出栈次序问题　　
1、一个栈(无穷大)的进栈序列为1,2,3,..n,有多少个不同的出栈序列?
2、有2n个人排成一行进入剧场。入场费5元。其中只有n个人有一张5元钞票，另外n人只有10元钞票，剧院无其它钞票，问有多少中方法使得只要有10元的人买票，售票处就有5元的钞票找零？(将持5元者到达视作将5元入栈，持10元者到达视作使栈中某5元出栈)。

将多边行划分为三角形问题　　
1、将一个凸多边形区域分成三角形区域的方法数?
2、一位大城市的律师在她住所以北n个街区和以东n个街区处工作。每天她走2n个街区去上班。如果她从不穿越（但可以碰到）从家到办公室的对角线，那么有多少条可能的道路？
3、在圆上选择2n个点,将这些点成对连接起来使得所得到的n条线段不相交的方法数?

给顶节点组成二叉树的问题　　给定N个节点，能构成多少种不同的二叉树？

一些笔试题
1、16个人按顺序去买烧饼，其中8个人每人身上只有一张5块钱，另外8个人每人身上只有一张10块钱。烧饼5块一个，开始时烧饼店老板身上没有钱。16个顾客互相不通气，每人只买一个。问这16个人共有多少种排列方法能避免找不开钱的情况出现。
h(8)=16!/(8!*9!)=1430，所以总数=h(8)*8！*8！=16!/9
2、在图书馆一共6个人在排队，3个还《面试宝典》一书，3个在借《面试宝典》一书，图书馆此时没有了面试宝典了，求他们排队的总数？
h(3)=6!/(3!*4!)=5，所以总数=h(3)*3!*3!=180

赞 (0)

相关推荐

  • 深入理解卡特兰数及其应用

    深入理解卡特兰数及其应用

    Catalan number,卡特兰数又称卡塔兰数,是组合数学中一个常出现在各种计数问题中出现的数列.以比利时的数学家欧仁·查理·卡塔兰 (1814–1894)命名. 令h(0)=1,h(1)=1,catalan数满足递推式:h(n)= h(0)*h(n-1)+h(1)*h(n-2) + ... + h(n-1)h(0) (n>=2) catalan数公式的一般是形式为: 递推关系: 它也满足  这提供了一个更快速的方法来计算卡塔兰数. 卡特兰数的应用n个元素顺序入栈,出栈顺序有多少种?此问题是

  • SQL Server 磁盘请求超时的833错误原因及解决方法

    SQL Server 磁盘请求超时的833错误原因及解决方法

    最近遇到一个SQL Server服务器响应极度缓慢,并且出现客户端请求报错的情况,在数据库中的errorlog中出现磁盘请求超过15s才完成的error消息. 对于此类问题,到底是存储系统或者磁盘的故障,还是SQL Server 自己的问题,亦或是应用程序引发的呢?又要如何解决? 本文将对引起此问题的某一方面的因素进行简单的分析,但是无法涵盖所有潜在的可能性,因此遇到类似问题还要做具体的分析. SQL Server中的磁盘请求超时 该错误的英文版的错误信息如下: SQL Server has e

  • C++实现LeetCode(96.独一无二的二叉搜索树)

    [LeetCode] 96. Unique Binary Search Trees 独一无二的二叉搜索树 Given n, how many structurally unique BST's (binary search trees) that store values 1 ... n? Example: Input: 3 Output: 5 Explanation: Given n = 3, there are a total of 5 unique BST's: 1         3  

  • 深入理解大数与高精度数的处理问题

    float和double型数据分别是单精度和双精度型数,他们的取值分别是3.4E+10的负38次方到3.4E+10的38次方,和1.7E+10的负308次方到1.7E+10的308次方. 那么对于float而言,只有6-7位的有效数字,怎么能装下可达3.4*10^(-38)这么大的数呢?同理,15-16位的double型,也无法装下1.7*10^(-308)这么大的数啊? 回答: float 6-7位指的是有效数字的位数(精度),而不是数值大小.例如,3.14159267有9位有效数字,数值却在

  • MySQL优化总结-查询总条数

    1.COUNT(*)和COUNT(COL) COUNT(*)通常是对主键进行索引扫描,而COUNT(COL)就不一定了,另外前者是统计表中的所有符合的纪录总数,而后者是计算表中所有符合的COL的纪录数.还有有区别的. 优化总结,对于MyISAM表来说: 1.任何情况下SELECT COUNT(*) FROM tablename是最优选择: 2.尽量减少SELECT COUNT(*) FROMtablename WHERE COL = 'value' 这种查询: 3.杜绝SELECT COUNT(

  • 深入理解PHP中mt_rand()随机数的安全

    前言 在前段时间挖了不少跟mt_rand()相关的安全漏洞,基本上都是错误理解随机数用法导致的.这里又要提一下php官网manual的一个坑,看下关于mt_rand()的介绍:中文版^cn 英文版^en,可以看到英文版多了一块黄色的 Caution 警告 This function does not generate cryptographically secure values, and should not be used for cryptographic purposes. If you

  • Base64编码的深入认识与理解

    Base64编码的深入认识与理解

    Base64编码的深入认识与理解 之前在很多业务中都有见过或者用到过Base64编码,但一直一知半解,没有对它有一个深入的认识和理解.今天就来聊一聊Base64编码的问题. 首先要明确的是,Base64是一种可逆的编码方式,提到编码方式,我们首先想到的肯定是Ascii.GBK.Unicode这些常用的编码方法,那么Base64与这些编码方式有什么不同呢? 简单来将,Base64就是一种用64个Ascii字符来表示任意二进制数据的方法.主要用于将不可打印的字符转换成可打印字符,或者简单的说将二进制

  • 深入理解JavaScript系列(1) 编写高质量JavaScript代码的基本要点

    具体一点就是编写高质量JavaScript的一些要素,例如避免全局变量,使用单变量声明,在循环中预缓存length(长度),遵循代码阅读,以及更多. 此摘要也包括一些与代码不太相关的习惯,但对整体代码的创建息息相关,包括撰写API文档.执行同行评审以及运行JSLint.这些习惯和最佳做法可以帮助你写出更好的,更易于理解和维护的代码,这些代码在几个月或是几年之后再回过头看看也是会觉得很自豪的. 书写可维护的代码(Writing Maintainable Code ) 软件bug的修复是昂贵的,并且

  • VBS 两数相加取值问题分析

    一个昵称为预言家晚报的朋友很喜欢玩SOSO问问,等级LV10,已经算比较高了.晚上挂QQ的时候,看到他的问问有更新,就点进去看了一下,问题是: 我写了如下一段VBS 复制代码 代码如下: dim a,b,c a=inputbox("a","please input") b=inputbox("b","please input") c=a+b msgbox(c) 可是最后结果是11,我知道肯定是倒数第二行的"+&quo

  • Nginx限制某个IP同一时间段的访问次数和请求数示例代码

    nginx可以通过ngx_http_limit_conn_module和ngx_http_limit_req_module配置来限制ip在同一时间段的访问次数. ngx_http_limit_conn_module:该模块用于限制每个定义的密钥的连接数,特别是单个IP​​地址的连接数．使用limit_conn_zone和limit_conn指令． ngx_http_limit_req_module:用于限制每一个定义的密钥的请求的处理速率,特别是从一个单一的IP地址的请求的处理速率.使用"泄漏桶

随机推荐