Python实现8个概率分布公式的方法详解

目录

• 前言
• 1.均匀分布
• 2.高斯分布
• 3.对数正态分布
• 4.泊松分布
• 5.指数分布
• 6.二项分布
• 7.学生 t 分布
• 8.卡方分布

前言

在本文中，我们将介绍一些常见的分布并通过Python 代码进行可视化以直观地显示它们。

概率和统计知识是数据科学和机器学习的核心； 我们需要统计和概率知识来有效地收集、审查、分析数据。

现实世界中有几个现象实例被认为是统计性质的（即天气数据、销售数据、财务数据等）。这意味着在某些情况下，我们已经能够开发出方法来帮助我们通过可以描述数据特征的数学函数来模拟自然。

“概率分布是一个数学函数，它给出了实验中不同可能结果的发生概率。”

了解数据的分布有助于更好地模拟我们周围的世界。它可以帮助我们确定各种结果的可能性，或估计事件的可变性。所有这些都使得了解不同的概率分布在数据科学和机器学习中非常有价值。

1.均匀分布

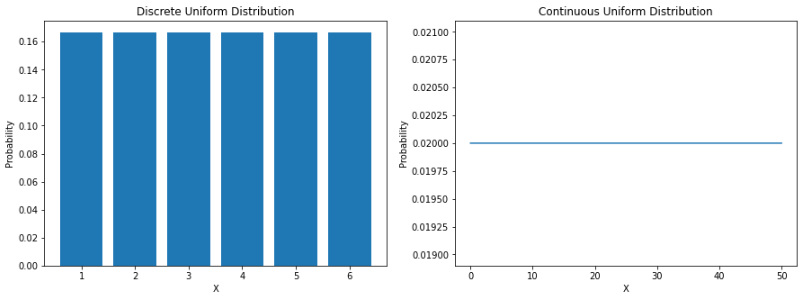
最直接的分布是均匀分布。均匀分布是一种概率分布，其中所有结果的可能性均等。例如，如果我们掷一个公平的骰子，落在任何数字上的概率是 1/6。这是一个离散的均匀分布。

但是并不是所有的均匀分布都是离散的——它们也可以是连续的。它们可以在指定范围内取任何实际值。a 和 b 之间连续均匀分布的概率密度函数 (PDF) 如下：

让我们看看如何在 Python 中对它们进行编码：

import numpy as np  
import matplotlib.pyplot as plt 
from scipy import stats 
 
# for continuous  
a = 0 
b = 50 
size = 5000 
 
X_continuous = np.linspace(a, b, size) 
continuous_uniform = stats.uniform(loc=a, scale=b) 
continuous_uniform_pdf = continuous_uniform.pdf(X_continuous) 
 
# for discrete 
X_discrete = np.arange(1, 7) 
discrete_uniform = stats.randint(1, 7) 
discrete_uniform_pmf = discrete_uniform.pmf(X_discrete)  
 
# plot both tables 
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(15,5)) 
# discrete plot 
ax[0].bar(X_discrete, discrete_uniform_pmf) 
ax[0].set_xlabel("X") 
ax[0].set_ylabel("Probability") 
ax[0].set_title("Discrete Uniform Distribution") 
# continuous plot 
ax[1].plot(X_continuous, continuous_uniform_pdf) 
ax[1].set_xlabel("X") 
ax[1].set_ylabel("Probability") 
ax[1].set_title("Continuous Uniform Distribution") 
plt.show()

2.高斯分布

高斯分布可能是最常听到也熟悉的分布。它有几个名字：有人称它为钟形曲线，因为它的概率图看起来像一个钟形，有人称它为高斯分布，因为首先描述它的德国数学家卡尔·高斯命名，还有一些人称它为正态分布，因为早期的统计学家 注意到它一遍又一遍地再次发生。

正态分布的概率密度函数如下：

σ 是标准偏差，μ 是分布的平均值。要注意的是，在正态分布中，均值、众数和中位数都是相等的。

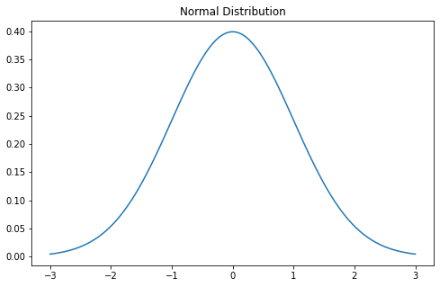
当我们绘制正态分布的随机变量时，曲线围绕均值对称——一半的值在中心的左侧，一半在中心的右侧。并且，曲线下的总面积为 1。

mu = 0 
variance = 1 
sigma = np.sqrt(variance) 
x = np.linspace(mu - 3*sigma, mu + 3*sigma, 100) 
 
plt.subplots(figsize=(8, 5)) 
plt.plot(x, stats.norm.pdf(x, mu, sigma)) 
plt.title("Normal Distribution") 
plt.show()

对于正态分布来说。经验规则告诉我们数据的百分比落在平均值的一定数量的标准偏差内。这些百分比是：

• 68% 的数据落在平均值的一个标准差内。
• 95% 的数据落在平均值的两个标准差内。
• 99.7% 的数据落在平均值的三个标准差范围内。

3.对数正态分布

对数正态分布是对数呈正态分布的随机变量的连续概率分布。因此，如果随机变量 X 是对数正态分布的，则 Y = ln(X) 具有正态分布。

这是对数正态分布的 PDF：

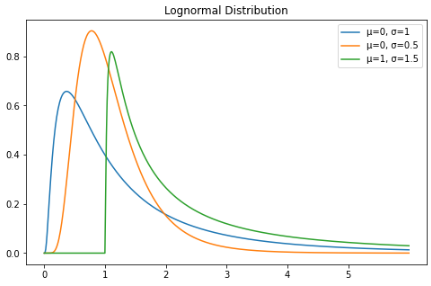
对数正态分布的随机变量只取正实数值。因此，对数正态分布会创建右偏曲线。

让我们在 Python 中绘制它：

X = np.linspace(0, 6, 500) 
 
std = 1 
mean = 0 
lognorm_distribution = stats.lognorm([std], loc=mean) 
lognorm_distribution_pdf = lognorm_distribution.pdf(X) 
 
fig, ax = plt.subplots(figsize=(8, 5)) 
plt.plot(X, lognorm_distribution_pdf, label="μ=0, σ=1") 
ax.set_xticks(np.arange(min(X), max(X))) 
 
std = 0.5 
mean = 0 
lognorm_distribution = stats.lognorm([std], loc=mean) 
lognorm_distribution_pdf = lognorm_distribution.pdf(X) 
plt.plot(X, lognorm_distribution_pdf, label="μ=0, σ=0.5") 
 
std = 1.5 
mean = 1 
lognorm_distribution = stats.lognorm([std], loc=mean) 
lognorm_distribution_pdf = lognorm_distribution.pdf(X) 
plt.plot(X, lognorm_distribution_pdf, label="μ=1, σ=1.5") 
 
plt.title("Lognormal Distribution") 
plt.legend() 
plt.show()

4.泊松分布

泊松分布以法国数学家西蒙·丹尼斯·泊松的名字命名。这是一个离散的概率分布，这意味着它计算具有有限结果的事件——换句话说，它是一个计数分布。因此，泊松分布用于显示事件在指定时期内可能发生的次数。

如果一个事件在时间上以固定的速率发生，那么及时观察到事件的数量（n）的概率可以用泊松分布来描述。例如，顾客可能以每分钟 3 次的平均速度到达咖啡馆。我们可以使用泊松分布来计算 9 个客户在 2 分钟内到达的概率。

下面是概率质量函数公式：

λ 是一个时间单位的事件率——在我们的例子中，它是 3。k 是出现的次数——在我们的例子中，它是 9。这里可以使用 Scipy 来完成概率的计算。

from scipy import stats 

print(stats.poisson.pmf(k=9, mu=3)) 

输出：

0.002700503931560479

泊松分布的曲线类似于正态分布，λ 表示峰值。

X = stats.poisson.rvs(mu=3, size=500) 
 
plt.subplots(figsize=(8, 5)) 
plt.hist(X, density=True, edgecolor="black") 
plt.title("Poisson Distribution") 
plt.show()

5.指数分布

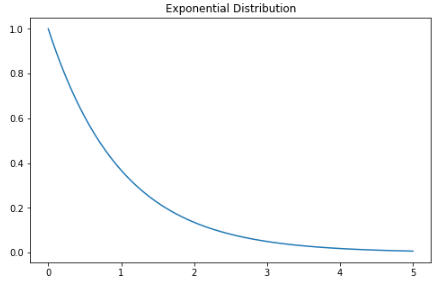
指数分布是泊松点过程中事件之间时间的概率分布。指数分布的概率密度函数如下：

λ 是速率参数，x 是随机变量。

X = np.linspace(0, 5, 5000) 
 
exponetial_distribtuion = stats.expon.pdf(X, loc=0, scale=1) 
 
plt.subplots(figsize=(8,5)) 
plt.plot(X, exponetial_distribtuion) 
plt.title("Exponential Distribution") 
plt.show()

6.二项分布

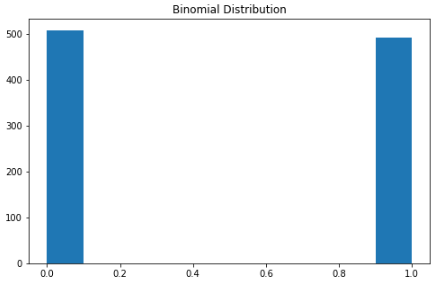
可以将二项分布视为实验中成功或失败的概率。有些人也可能将其描述为抛硬币概率。

参数为 n 和 p 的二项式分布是在 n 个独立实验序列中成功次数的离散概率分布，每个实验都问一个是 - 否问题，每个实验都有自己的布尔值结果：成功或失败。

本质上，二项分布测量两个事件的概率。一个事件发生的概率为 p，另一事件发生的概率为 1-p。

这是二项分布的公式：

• P = 二项分布概率
• = 组合数
• x = n次试验中特定结果的次数
• p = 单次实验中，成功的概率
• q = 单次实验中，失败的概率
• n = 实验的次数

可视化代码如下：

X = np.random.binomial(n=1, p=0.5, size=1000) 
 
plt.subplots(figsize=(8, 5)) 
plt.hist(X) 
plt.title("Binomial Distribution") 
plt.show()

7.学生 t 分布

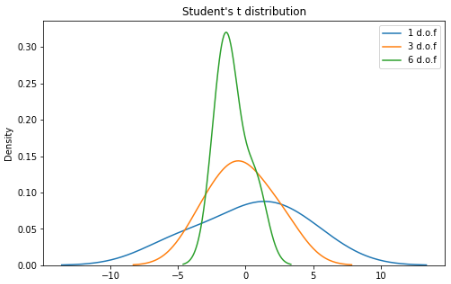
学生 t 分布（或简称 t 分布）是在样本量较小且总体标准差未知的情况下估计正态分布总体的均值时出现的连续概率分布族的任何成员。它是由英国统计学家威廉·西利·戈塞特（William Sealy Gosset）以笔名“student”开发的。

PDF如下：

n 是称为“自由度”的参数，有时可以看到它被称为“d.o.f.” 对于较高的 n 值，t 分布更接近正态分布。

import seaborn as sns 
from scipy import stats 
 
X1 = stats.t.rvs(df=1, size=4) 
X2 = stats.t.rvs(df=3, size=4) 
X3 = stats.t.rvs(df=9, size=4) 
 
plt.subplots(figsize=(8,5)) 
sns.kdeplot(X1, label = "1 d.o.f") 
sns.kdeplot(X2, label = "3 d.o.f") 
sns.kdeplot(X3, label = "6 d.o.f") 
plt.title("Student's t distribution") 
plt.legend() 
plt.show()

8.卡方分布

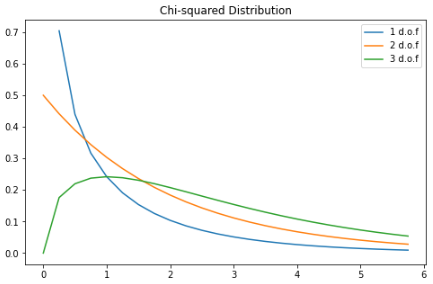
卡方分布是伽马分布的一个特例；对于 k 个自由度，卡方分布是一些独立的标准正态随机变量的 k 的平方和。

PDF如下：

这是一种流行的概率分布，常用于假设检验和置信区间的构建。

在 Python 中绘制一些示例图：

X = np.arange(0, 6, 0.25) 
 
plt.subplots(figsize=(8, 5)) 
plt.plot(X, stats.chi2.pdf(X, df=1), label="1 d.o.f") 
plt.plot(X, stats.chi2.pdf(X, df=2), label="2 d.o.f") 
plt.plot(X, stats.chi2.pdf(X, df=3), label="3 d.o.f") 
plt.title("Chi-squared Distribution") 
plt.legend() 
plt.show()

掌握统计学和概率对于数据科学至关重要。在本文展示了一些常见且常用的分布，希望对你有所帮助。

以上就是Python实现8个概率分布公式的方法详解的详细内容，更多关于Python概率分布的资料请关注我们其它相关文章！