java实现Dijkstra算法

本文实例为大家分享了java实现Dijkstra算法的具体代码，供大家参考，具体内容如下

1 问题描述

何为Dijkstra算法？

Dijkstra算法功能：给出加权连通图中一个顶点，称之为起点，找出起点到其它所有顶点之间的最短距离。

Dijkstra算法思想：采用贪心法思想，进行n-1次查找（PS:n为加权连通图的顶点总个数，除去起点，则剩下n-1个顶点），第一次进行查找，找出距离起点最近的一个顶点，标记为已遍历；下一次进行查找时，从未被遍历中的顶点寻找距离起点最近的一个顶点， 标记为已遍历；直到n-1次查找完毕，结束查找，返回最终结果。

2 解决方案

2.1 使用Dijkstra算法得到最短距离示例

此处借用文末参考资料1博客中一个插图（PS：个人感觉此图描述简单易懂）：

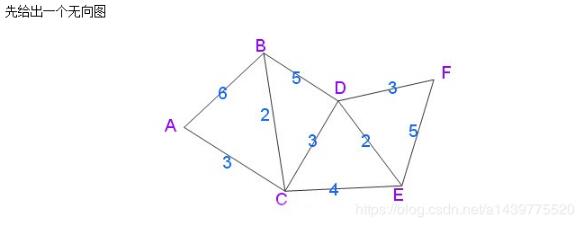
2.2 具体编码

Dijkstra复杂度是O(N^2)，如果用binary heap优化可以达到O((E+N)logN)，用fibonacci heap可以优化到O(NlogN+E) 。

注意，Dijkstra算法只能应用于不含负权值的图。因为在大多数应用中这个条件都满足，所以这种局限性并没有影响Dijkstra算法的广泛应用。

其次，大家要注意把Dijkstra算法与寻找最小生成树的Prim算法区分开来。两者都是运行贪心法思想，但是Dijkstra算法是比较路径的长度，所以必须把起点到相应顶点之间的边的权重相加，而Prim算法则是直接比较相应边给定的权重。

下面的代码时间复杂度为O(N^2)，代码中所用图为2.1使用Dijkstra算法得到最短距离示例中所给的图。

package com.liuzhen.chapter9;

public class Dijkstra {
  /*
   * 参数adjMatrix:为图的权重矩阵，权值为-1的两个顶点表示不能直接相连
   * 函数功能：返回顶点0到其它所有顶点的最短距离，其中顶点0到顶点0的最短距离为0
   */
  public int[] getShortestPaths(int[][] adjMatrix) {
    int[] result = new int[adjMatrix.length];  //用于存放顶点0到其它顶点的最短距离
    boolean[] used = new boolean[adjMatrix.length]; //用于判断顶点是否被遍历
    used[0] = true; //表示顶点0已被遍历
    for(int i = 1;i < adjMatrix.length;i++) {
      result[i] = adjMatrix[0][i];
      used[i] = false;
    }

    for(int i = 1;i < adjMatrix.length;i++) {
      int min = Integer.MAX_VALUE;  //用于暂时存放顶点0到i的最短距离，初始化为Integer型最大值
      int k = 0;
      for(int j = 1;j < adjMatrix.length;j++) { //找到顶点0到其它顶点中距离最小的一个顶点
        if(!used[j] && result[j] != -1 && min > result[j]) {
          min = result[j];
          k = j;
        }
      }
      used[k] = true;  //将距离最小的顶点，记为已遍历
      for(int j = 1;j < adjMatrix.length;j++) { //然后，将顶点0到其它顶点的距离与加入中间顶点k之后的距离进行比较，更新最短距离
        if(!used[j]) { //当顶点j未被遍历时
          //首先，顶点k到顶点j要能通行；这时，当顶点0到顶点j的距离大于顶点0到k再到j的距离或者顶点0无法直接到达顶点j时，更新顶点0到顶点j的最短距离
          if(adjMatrix[k][j] != -1 && (result[j] > min + adjMatrix[k][j] || result[j] == -1))
            result[j] = min + adjMatrix[k][j];
        }
      }
    }
    return result;
  }

  public static void main(String[] args) {
    Dijkstra test = new Dijkstra();
    int[][] adjMatrix = {{0,6,3,-1,-1,-1},
        {6,0,2,5,-1,-1},
        {3,2,0,3,4,-1},
        {-1,5,3,0,2,3},
        {-1,-1,4,2,0,5},
        {-1,-1,-1,3,5,0}};
    int[] result = test.getShortestPaths(adjMatrix);
    System.out.println("顶点0到图中所有顶点之间的最短距离为：");
    for(int i = 0;i < result.length;i++)
      System.out.print(result[i]+" ");
  }
}

运行结果：

顶点0到图中所有顶点之间的最短距离为：
0 5 3 6 7 9

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持我们。