深入了解Java数据结构和算法之堆

目录

• 1、堆的定义
• 2、遍历和查找
• 3、移除
• 4、插入
• 5、完整的Java堆代码
• 总结

1、堆的定义

①、它是完全二叉树，除了树的最后一层节点不需要是满的，其它的每一层从左到右都是满的。注意下面两种情况，第二种最后一层从左到右中间有断隔，那么也是不完全二叉树。

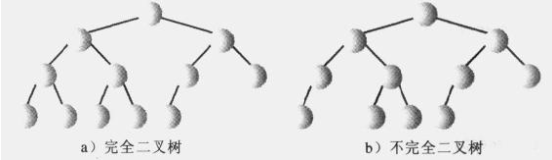
②、它通常用数组来实现。　　

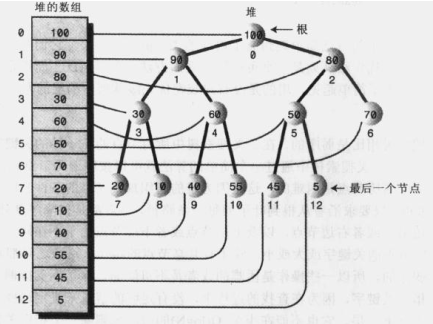
这种用数组实现的二叉树，假设节点的索引值为index，那么：

节点的左子节点是 2*index+1，

节点的右子节点是 2*index+2，

节点的父节点是 （index-1）/2。

③、堆中的每一个节点的关键字都大于（或等于）这个节点的子节点的关键字。

这里要注意堆和前面说的二叉搜索树的区别，二叉搜索树中所有节点的左子节点关键字都小于右子节点关键字，在二叉搜索树中通过一个简单的算法就可以按序遍历节点。但是在堆中，按序遍历节点是很困难的，如上图所示，堆只有沿着从根节点到叶子节点的每一条路径是降序排列的，指定节点的左边节点或者右边节点，以及上层节点或者下层节点由于不在同一条路径上，他们的关键字可能比指定节点大或者小。所以相对于二叉搜索树，堆是弱序的。

2、遍历和查找

前面我们说了，堆是弱序的，所以想要遍历堆是很困难的，基本上，堆是不支持遍历的。

对于查找，由于堆的特性，在查找的过程中，没有足够的信息来决定选择通过节点的两个子节点中的哪一个来选择走向下一层，所以也很难在堆中查找到某个关键字。

因此，堆这种组织似乎非常接近无序，不过，对于快速的移除最大（或最小）节点，也就是根节点，以及能快速插入新的节点，这两个操作就足够了。

3、移除

移除是指删除关键字最大的节点（或最小），也就是根节点。

根节点在数组中的索引总是0，即maxNode = heapArray[0];

移除根节点之后，那树就空了一个根节点，也就是数组有了一个空的数据单元，这个空单元我们必须填上。

第一种方法：将数组所有数据项都向前移动一个单元，这比较费时。

第二种方法：

• ①、移走根
• ②、把最后一个节点移动到根的位置
• ③、一直向下筛选这个节点，直到它在一个大于它的节点之下，小于它的节点之上为止。

具体步骤如下：

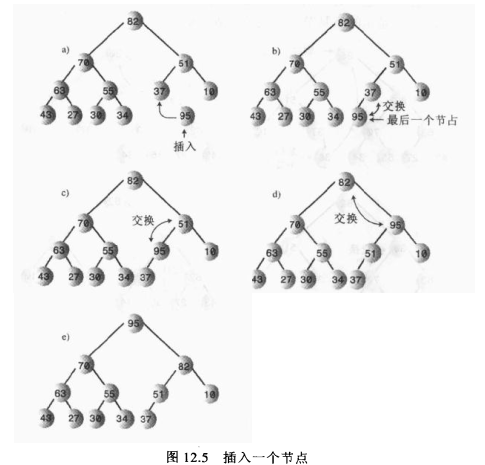
图a表示把最后一个节点移到根节点，图b、c、d表示将节点向下筛选到合适的位置，它的合适位置在最底层（有时候可能在中间），图e表示节点在正确位置的情景。

注意：向下筛选的时候，将目标节点和其子节点比较，谁大就和谁交换位置。

4、插入

插入节点也很容易，插入时，选择向上筛选，节点初始时插入到数组最后第一个空着的单元，数组容量大小增一。然后进行向上筛选的算法。

注意：向上筛选和向下不同，向上筛选只用和一个父节点进行比较，比父节点小就停止筛选了。

5、完整的Java堆代码

首先我们要知道用数组表示堆的一些要点。若数组中节点的索引为x，则：

节点的左子节点是 2*index+1，

节点的右子节点是 2*index+2，

节点的父节点是 （index-1）/2。

注意："/" 这个符号，应用于整数的算式时，它执行整除，且得到是是向下取整的值。

package com.ys.tree.heap;

public class Heap {

    private Node[] heapArray;
    private int maxSize;
    private int currentSize;

    public Heap(int mx) {
        maxSize = mx;
        currentSize = 0;
        heapArray = new Node[maxSize];
    }

    public boolean isEmpty() {
        return (currentSize == 0)? true : false;
    }

    public boolean isFull() {
        return (currentSize == maxSize)? true : false;
    }

    public boolean insert(int key) {
        if(isFull()) {
            return false;
        }
        Node newNode = new Node(key);
        heapArray[currentSize] = newNode;
        trickleUp(currentSize++);
        return true;
    }
    //向上调整
    public void trickleUp(int index) {
        int parent = (index - 1) / 2; //父节点的索引
        Node bottom = heapArray[index]; //将新加的尾节点存在bottom中
        while(index > 0 && heapArray[parent].getKey() < bottom.getKey()) {
            heapArray[index] = heapArray[parent];
            index = parent;
            parent = (parent - 1) / 2;
        }
        heapArray[index] = bottom;
    }

    public Node remove() {
        Node root = heapArray[0];
        heapArray[0] = heapArray[--currentSize];
        trickleDown(0);
        return root;
    }
    //向下调整
    public void trickleDown(int index) {
        Node top = heapArray[index];
        int largeChildIndex;
        while(index < currentSize/2) { //while node has at least one child
            int leftChildIndex = 2 * index + 1;
            int rightChildIndex = leftChildIndex + 1;
            //find larger child
            if(rightChildIndex < currentSize &&  //rightChild exists?
                    heapArray[leftChildIndex].getKey() < heapArray[rightChildIndex].getKey()) {
                largeChildIndex = rightChildIndex;
            }
            else {
                largeChildIndex = leftChildIndex;
            }
            if(top.getKey() >= heapArray[largeChildIndex].getKey()) {
                break;
            }
            heapArray[index] = heapArray[largeChildIndex];
            index = largeChildIndex;
        }
        heapArray[index] = top;
    }
    //根据索引改变堆中某个数据
    public boolean change(int index, int newValue) {
        if(index < 0 || index >= currentSize) {
            return false;
        }
        int oldValue = heapArray[index].getKey();
        heapArray[index].setKey(newValue);
        if(oldValue < newValue) {
            trickleUp(index);
        }
        else {
            trickleDown(index);
        }
        return true;
    }

    public void displayHeap() {
        System.out.println("heapArray(array format): ");
        for(int i = 0; i < currentSize; i++) {
            if(heapArray[i] != null) {
                System.out.print(heapArray[i].getKey() + " ");
            }
            else {
                System.out.print("--");
            }
        }
    }
}
class Node {
    private int iData;
    public Node(int key) {
        iData = key;
    }

    public int getKey() {
        return iData;
    }

    public void setKey(int key) {
        iData = key;
    }
}

总结

本篇文章就到这里了，希望能够给你带来帮助，也希望您能够多多关注我们的更多内容!