Java实现动态规划背包问题

目录

• 前言
• 一、原理
• 1.1 最优子结构性质
• 1.2 递归关系
• 二、算法描述
• 2.1 算法描述
• 2.2 图解
• 2.3 构造最优解
• 三、 0 − 1 0-1 0−1 背包问题相关题目
• 3.1 题目
• 3.2 源程序(Java求解 0 − 1 0-1 0−1背包问题)
• 3.3 运行结果
• 总结

前言

给定 n n n 种物品和一个背包。物品 i i i 的重量是 w i wi wi，其价值为 v i vi vi，背包的容量为 c c c。问应如何选择装入背包的物品，使得装入背包中物品的总价值最大？

一、原理

0 − 0 - 0− 1 1 1 背包问题是一个特殊的整数规划问题。

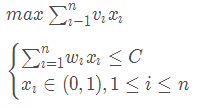
1.1 最优子结构性质

​

1.2 递归关系

设所给 0 − 1 0-1 0−1 背包问题的子问题的最优值为 m(i，j)，即 m(i，j)是背包容量为 j，可选择物品为 i，i+1，…，n 时 0-1背包问题的最优值。由 0-1背包问题的最优子结构性质，可以建立计算 m(i，j)的递归式如下：

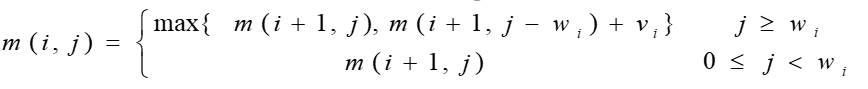
二、算法描述

2.1 算法描述

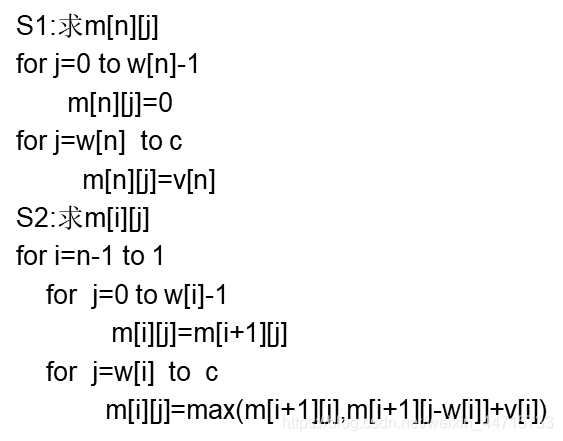
伪代码：

2.2 图解

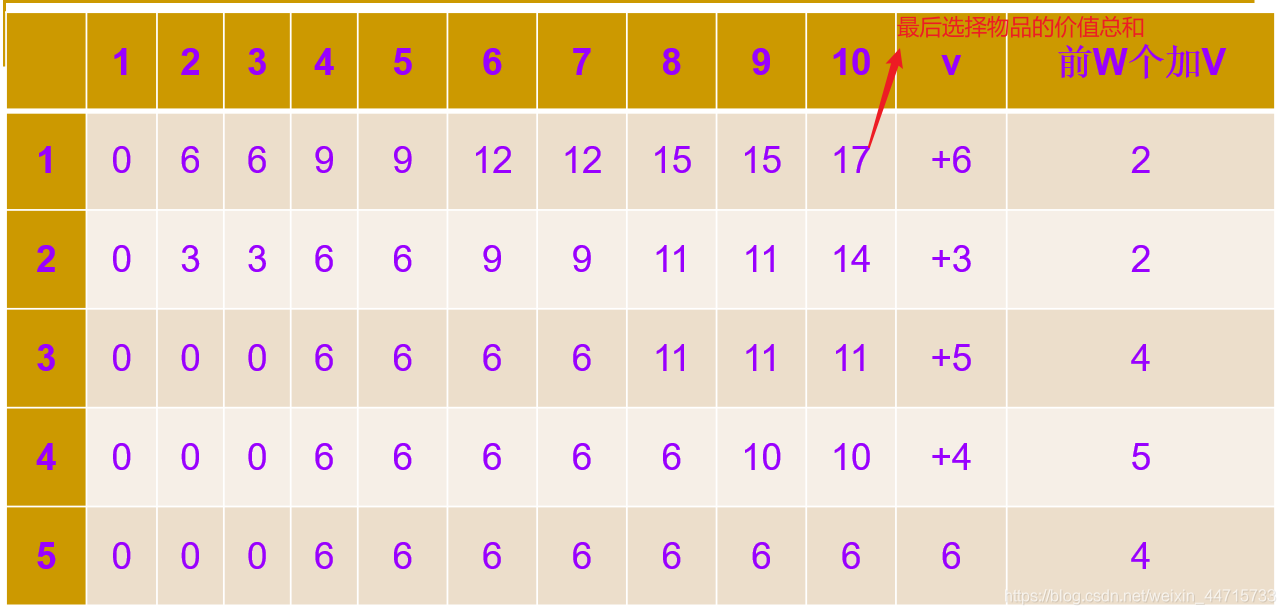
2.3 构造最优解

三、 0 − 1 0-1 0−1 背包问题相关题目

3.1 题目

已知有5个物体，它们的重量分别为：2，2，4，5，4，各物体的价值依次为6，3，5，4，6，背包大小为10，使用动态规划法求矩阵m[i][j]，并给出最优解。修改数据为：5个物体，它们的重量分别为：1，1，2，3，2，各物体的价值依次为6，3，5，4，6，背包大小为6，使用动态规划法求矩阵m[i][j]，并给出最优解

3.2 源程序(Java求解 0 − 1 0-1 0−1背包问题)

/**
 * 0-1背包问题（动态规划法求解）
 */
public class E3_9 {
    //物品的个数+1(第一个数我写成0)
    static int N = 6;
    //static int C = 7;
    static int C = 11;
    /**
     * 程序的入口
     * @param args
     */
    public static void main(String[] args) {
        //int n = N-1;
        //背包的容量
        int c = C-1;
        int i;
        //物体的重量
        //int w[] = new int[N];
        int w[] = new int[]{0,2,2,4,5,4};
        //int w[] = new int[]{0,1,1,2,3,2};
        //物体的价值
        //int v[] = new int[N];
        int v[] = new int[]{0,6,3,5,4,6};
        //动态规划法求解过程的矩阵
        int m[][] = new int[N][C];
        //选择的结果
        int x[] = new int [N];

        // for (i = 1; i < N; i++) {
        //     w[i] = 1+(int) (Math.random()*5);
        //     v[i] = 1+(int) (Math.random()*10);
        // }

        knapsack(v,w,c,m);
        traceback(m,w,c,x);

        System.out.printf("背包能装的最大价值为："+"%d  \n ",m[1][c]);
        for (i = 1; i <= c; i++) {
            System.out.printf("%2d  \t",i);
        }
        System.out.printf("重量 价值\n");

        for (i = 1; i < N; i++) {
            System.out.printf("%d:",i);
            for (int j = 1; j <= c; j++) {
                System.out.printf("%2d  \t",m[i][j]);
            }
            System.out.printf("%2d%4d\n",w[i],v[i]);
        }
        System.out.printf("\n\n物品的重量");
        for (i = 1; i < N; i++) {
            System.out.printf("%2d   \t",w[i]);
        }
        System.out.printf("\n物品的价值");
        for (i = 1; i < N; i++) {
            System.out.printf("%2d   \t",v[i]);
        }
        System.out.printf("\n选择的结果");
        for (i = 1; i < N; i++) {
            System.out.printf("%2d   \t",x[i]);
        }
        System.out.printf("\n");
    }

    /**
     * 由0-1背包问题的最优子结构性质建立的递归式
     * @param v 存储物品价值的数组
     * @param w 存储物品重量的数组
     * @param c 背包容量
     * @param m 动态规划法求解过程的矩阵
     */
    public static void knapsack(int []v,int []w,int c,int [][]m){
        int n=v.length-1;
        int jMax=Math.min(w[n]-1,c);
        for(int j=0;j<=jMax;j++)  m[n][j]=0;
        for(int j=w[n];j<=c;j++)  m[n][j]=v[n];
        for(int i=n-1;i>0;i--){
            jMax=Math.min(w[i]-1,c);
            for(int j=0;j<=jMax;j++)
                m[i][j]=m[i+1][j];
            for(int j=w[i];j<=c;j++)
                m[i][j]=Math.max(m[i+1][j],m[i+1][j-w[i]]+v[i]);
        }
        //m[1][c]=m[2][c];
        //对于i=1时的两种情况
        if(c>=w[1])
            m[1][c]=Math.max(m[2][c],m[2][c-w[1]]+v[1]);
        else
            m[1][c]=m[2][c];
    }

    /**
     * 构造最优解
     * @param m 动态规划法求解过程的矩阵
     * @param w 存储物体的重量的数组
     * @param c 背包容量
     * @param x 存储选择结果的数组
     */
    public static void traceback(int [][]m,int []w,int c,int []x){
        int n=w.length-1;
        for(int i=1;i<n;i++)
            if(m[i][c]==m[i+1][c])
                x[i]=0;
            else {
                x[i]=1;
                c-=w[i];
            }
        x[n]=(m[n][c]>0)?1:0;
    }
}

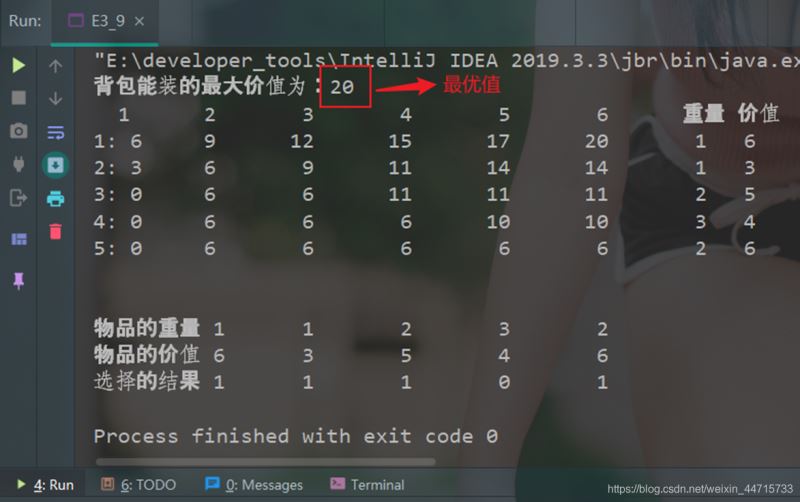
3.3 运行结果

总结

动态规划基本步骤

• 找出最优解的性质，并刻划其结构特征。
• 递归地定义最优值。
• 以自底向上的方式计算出最优值。
• 根据计算最优值时得到的信息，构造最优解。

到此这篇关于Java实现动态规划背包问题的文章就介绍到这了,更多相关java动态规划内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！