线段树详解以及C++实现代码

目录

• 应用场景
• 算法思想
• 查询操作
• 修改操作
• 算法实现
• 建树
• 查询
• 修改
• 总结

应用场景

假设有这样的问题：有n个数，m次操作，操作分为：修改某一个数或者查询一段区间的值

分析下，如果针对数组元素的修改可以是O(1)完成，求某个区间值需要O(n)才可以完成，如果m和n都很大的情况，这个复杂度就很难接受了。

我们之前学过的前缀和算法可以解决区间求和的问题，并且时间复杂度是O(1)，但如果涉及到修改操作，前缀和数组都需要重新计算，时间复杂度也是O(n)

有没有什么办法可以兼顾以上两种操作，并且可以将时间复杂度降低？

这就是我们要学习的线段树！把修改和查询的时间复杂度都降到O(logn)！！！

算法思想

先来看下线段树长什么样：

有以下数组（为方便计算，数组下标从1开始）

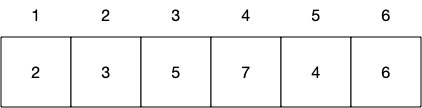
我们把它转换成线段树，是长这样的：

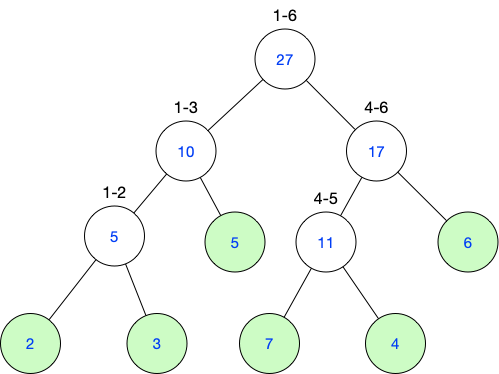
1）叶子结点（绿色）存的都是原数组元素的值

2）每个父结点是它的两个子节点的值的和

3）每个父结点记录它表示区间的范围，如上图的“1-2”表示1到2的区间

下面我们来看看线段树是如何降低操作复杂度的！

查询操作

例如我们需要查询2-5区间的和

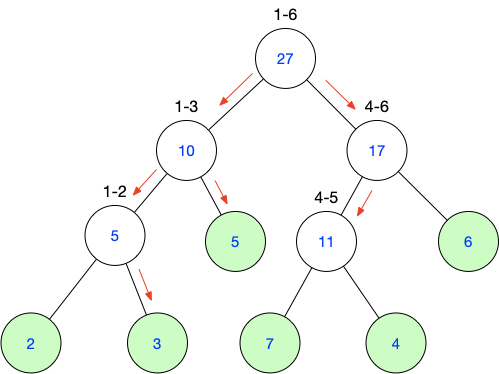
使用递归的思想：

2~5的和

=2~3的和+4~5的和

=3+5+4~5的和

=3+5+11

=19

总之，就是沿着线段树的划分把区间分开，再加到一块就行啦！

修改操作

例如，我们要把结点2的值由3->5，线段树需要沿着红色部分一个一个改，直到根结点：

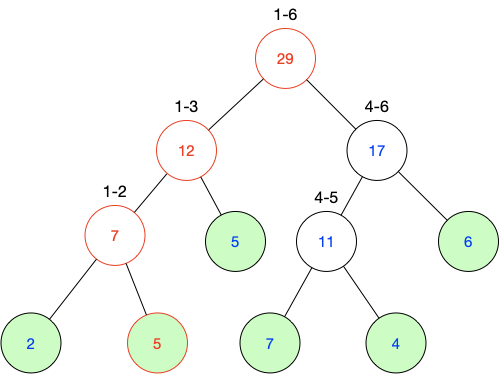
不管是修改操作还是查询操作，时间复杂度都是O(logn)

下一步我们来看怎么实现线段树！

算法实现

首先我们需要将原始数组建立成一颗线段树，然后在树的基础上提供查询和修改的操作。

建树

观察上图，我们发现线段树是一棵近似完全二叉树，利用完全二叉树的性质，我们就可以直接用一个数组来存它。

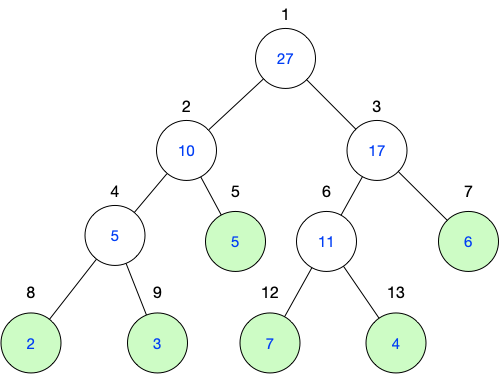
就像上图一样把各个节点标上号，如果根节点编号是n,那它的左子树编号是2n,右子树的编号是2n+1

所以说，知道了根节点的编号，我们就可以快速有效的找到左右子树的根节点

void build(int root,int start,int end){
    if(start == end){
        tree[root] = num[start];
        return;
    }
    int leftroot = root * 2;//左结点
    int rightroot = root * 2 + 1;//右结点
    int mid = (start+end)/2;
    build(leftroot,start,mid);//递归计算左结点
    build(rightroot,mid+1,end);//递归计算右结点
    tree[root] = tree[leftroot] + tree[rightroot];//根结点值=左根+右根
}

查询

int query(int root,int start,int end,int l,int r){
    if(l<=start && r>= end){
        return tree[root];
    }
    int leftroot = root * 2;
    int rightroot = root * 2 + 1;
    int mid = (start+end)/2;
    int sum = 0;
    if(l<=mid){
        sum += query(leftroot,start,mid,l,r);
    }
    if(r>mid){
        sum += query(rightroot,mid+1,end,l,r);
    }
    return sum;
}

修改

/**
* 修改[l,r]区间里的数，都加上k值
* @param root
* @param start
* @param end
* @param l
* @param r
* @param k
*/
void update(int root,int start,int end,int l,int r,int k){
    if(start == end){
        tree[root] += k;
        return;
    }
    int leftroot = root * 2;
    int rightroot = root * 2 + 1;
    int mid = (start+end)/2;
    if(l<=mid){
        update(leftroot,start,mid,l,r,k);
    }
    if(r>mid){
        update(rightroot,mid+1,end,l,r,k);
    }
    tree[root] = tree[leftroot] + tree[rightroot];
}

！！！：考虑下按区间修改元素值的复杂度？

注意事项：

1）我们在实现线段树时，实际存储肯定大于原始数组，我们一般让tree数组的长度为原始数据长度的3-4倍。

2）本文只是为了让大家学习线段树的实现原理，实际中我们可以将原始数组的start，end使用结构体存储，这样更简洁

总结

到此这篇关于线段树详解以及C++实现的文章就介绍到这了,更多相关C++实现线段树内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！