C语言设计前中后队列实例代码

目录

• 队列基本概念
• 1，数组实现
•  2，链表实现
•  总结

队列基本概念

队列是最常见的概念，日常生活经常需要排队，仔细观察队列会发现，队列是一种逻辑结构，是一种特殊的线性表。特殊在：

只能在固定的两端操作线性表

只要满足上述条件，那么这种特殊的线性表就会呈现出一种“先进先出”的逻辑，这种逻辑就被称为队列。

由于约定了只能在线性表固定的两端进行操作，于是给队列这种特殊的线性表的插入删除，起个特殊的名称：

队头：可以删除节点的一端

队尾：可以插入节点的一端

入队：将节点插入到队尾之后，函数名通常为enQueue()

出队：将队头节点从队列中剔除，函数名通常为outQueue()

取队头：取得队头元素，但不出队，函数名通常为front()

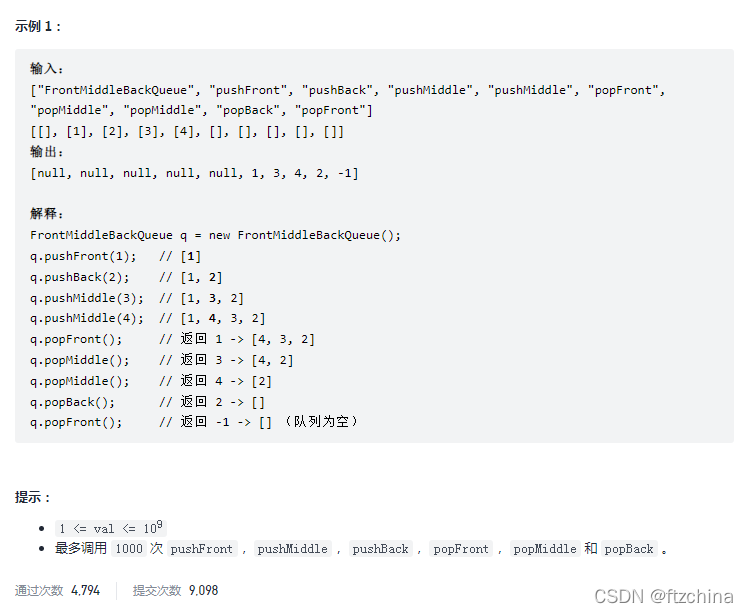
本题就是手撸数据结构中基本的队列结构，常用的有两种，一种是用链表实现，一种是数组实现。本文将会给出两种实现方式

1，数组实现

typedef struct {
    int value[1000];
    int len;
} FrontMiddleBackQueue;

FrontMiddleBackQueue* frontMiddleBackQueueCreate() {
    FrontMiddleBackQueue *queue = (FrontMiddleBackQueue *)malloc(sizeof(FrontMiddleBackQueue));
    memset(queue,0,sizeof(FrontMiddleBackQueue));
    return queue;
}

void insert(FrontMiddleBackQueue* obj, int pos, int val)
{
    //在pos位置插入val，则pos(从0开始)位置后的数统一向后挪一个位置,队列长度加1
    int i = 0;
    for(i=obj->len; i>pos; i--)
    {
        obj->value[i] = obj->value[i-1];
    }
    obj->value[pos] = val;
    obj->len++;
}

int pop(FrontMiddleBackQueue* obj, int pos)
{
    //弹出pos位置的val,则pos(从0开始)位置后向前统一挪一个位置，队列长度减一
    if(obj->len == 0)
        return -1;
    int i = 0;
    int popval = obj->value[pos]; //先将pos位置的数保存下来，不然下面的移位操作就覆盖了pos位置的值
    for(i=pos; i<obj->len-1; i++)
    {
        obj->value[i] = obj->value[i+1];
    }
    obj->len--;
    return popval;
}

void frontMiddleBackQueuePushFront(FrontMiddleBackQueue* obj, int val) {
    insert(obj,0,val);
}

void frontMiddleBackQueuePushMiddle(FrontMiddleBackQueue* obj, int val) {
    insert(obj,obj->len/2,val);
}

void frontMiddleBackQueuePushBack(FrontMiddleBackQueue* obj, int val) {
    insert(obj,obj->len,val);
}

int frontMiddleBackQueuePopFront(FrontMiddleBackQueue* obj) {
    return pop(obj,0);
}

int frontMiddleBackQueuePopMiddle(FrontMiddleBackQueue* obj) {
    return pop(obj,(obj->len-1)/2);
}

int frontMiddleBackQueuePopBack(FrontMiddleBackQueue* obj) {
    return pop(obj, obj->len-1);
}

void frontMiddleBackQueueFree(FrontMiddleBackQueue* obj) {
    free(obj);
}

/**
 * Your FrontMiddleBackQueue struct will be instantiated and called as such:
 * FrontMiddleBackQueue* obj = frontMiddleBackQueueCreate();
 * frontMiddleBackQueuePushFront(obj, val);

 * frontMiddleBackQueuePushMiddle(obj, val);

 * frontMiddleBackQueuePushBack(obj, val);

 * int param_4 = frontMiddleBackQueuePopFront(obj);

 * int param_5 = frontMiddleBackQueuePopMiddle(obj);

 * int param_6 = frontMiddleBackQueuePopBack(obj);

 * frontMiddleBackQueueFree(obj);
*/

运行结果

 2，链表实现

1，设计链表结构，链表维持一个头节点和尾结点，头节点始终在最前面并且头结点的data存储整个队列的节点数，尾结点始终是最后一个节点

2，设计插入节点函数和删除节点函数，push和pop操作只需要根据不同场景传入不同的参数即可完成统一的操作

typedef struct tag_Node {
    int data;
    struct tag_Node* next, *prev;
}Node;

typedef struct {
    Node* front;
    Node* rear;
} FrontMiddleBackQueue;

FrontMiddleBackQueue* frontMiddleBackQueueCreate() {
    FrontMiddleBackQueue* que = (FrontMiddleBackQueue *)malloc(sizeof(FrontMiddleBackQueue));
    que->front = (Node *)malloc(sizeof(Node));
    que->rear = (Node *)malloc(sizeof(Node));
    que->front->data = 0;
    que->front->next = NULL;
    que->rear->data = 0;
    que->rear->next = NULL;
    que->front->next = que->rear;
    que->rear->prev = que->front;

    return que;
}

void AddNode(FrontMiddleBackQueue* obj, Node *cur, int val)
{
    Node* addNode = (Node *)malloc(sizeof(Node));
    addNode->data = val;
    addNode->prev = cur->prev;
    addNode->next = cur;

    cur->prev->next = addNode;
    cur->prev = addNode;

    obj->front->data++;
    return;
}

Node* GetMiddleNode(FrontMiddleBackQueue* obj, bool isAdd)
{
    Node* tmp = obj->front->next;

    int len = isAdd ? (obj->front->data / 2) : ((obj->front->data - 1) / 2);
    for (int i = 0; i < len; i++) {
        tmp = tmp->next;
    }
    return tmp;
}

void frontMiddleBackQueuePushFront(FrontMiddleBackQueue* obj, int val) {
    AddNode(obj, obj->front->next, val);
    return;
}

void frontMiddleBackQueuePushMiddle(FrontMiddleBackQueue* obj, int val) {
    AddNode(obj, GetMiddleNode(obj, true), val);
    return;
}

void frontMiddleBackQueuePushBack(FrontMiddleBackQueue* obj, int val) {
    AddNode(obj, obj->rear, val);
    return;
}

int RemoveNode(FrontMiddleBackQueue* obj, Node* cur)
{
    if (obj->front->data == 0) {
        return -1;
    }
    cur->next->prev = cur->prev;
    cur->prev->next = cur->next;

    obj->front->data--;
    int item = cur->data;
    free(cur);
    return item;
}

int frontMiddleBackQueuePopFront(FrontMiddleBackQueue* obj) {
    return RemoveNode(obj, obj->front->next);
}

int frontMiddleBackQueuePopMiddle(FrontMiddleBackQueue* obj) {
    return RemoveNode(obj, GetMiddleNode(obj, false));
}

int frontMiddleBackQueuePopBack(FrontMiddleBackQueue* obj) {
    return RemoveNode(obj, obj->rear->prev);
}

void frontMiddleBackQueueFree(FrontMiddleBackQueue* obj) {
    while (RemoveNode(obj, obj->front->next) != -1);
    free(obj->front);
    free(obj->rear);
    free(obj);
    return;
}

/**
 * Your FrontMiddleBackQueue struct will be instantiated and called as such:
 * FrontMiddleBackQueue* obj = frontMiddleBackQueueCreate();
 * frontMiddleBackQueuePushFront(obj, val);

 * frontMiddleBackQueuePushMiddle(obj, val);

 * frontMiddleBackQueuePushBack(obj, val);

 * int param_4 = frontMiddleBackQueuePopFront(obj);

 * int param_5 = frontMiddleBackQueuePopMiddle(obj);

 * int param_6 = frontMiddleBackQueuePopBack(obj);

 * frontMiddleBackQueueFree(obj);
*/

运行结果：

 总结

到此这篇关于C语言设计前中后队列的文章就介绍到这了,更多相关C语言设计前中后队列内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！