算法系列15天速成 第九天 队列

一：概念

队列是一个”先进先出“的线性表，牛X的名字就是“First in First Out(FIFO)”，生活中有很多这样的场景，比如读书的时候去食堂打饭时的”排队“。当然我们拒绝插队。

二：存储结构

前几天也说过，线性表有两种”存储结构“，① 顺序存储,②链式存储。当然“队列”也脱离不了这两种服务，这里我就分享一下“顺序存储”。

顺序存储时，我们会维护一个叫做”head头指针“和”tail尾指针“，分别指向队列的开头和结尾。

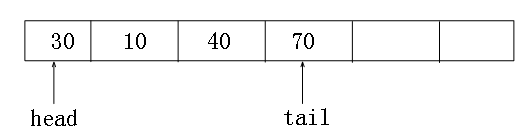
代码段如下：

代码如下:

#region 队列的数据结构
    /// <summary>
/// 队列的数据结构
/// </summary>
/// <typeparam name="T"></typeparam>
    public class SeqQueue<T>
    {
        private const int maxSize = 100;

public int MaxSize
        {
            get { return maxSize; }
        }

/// <summary>
/// 顺序队列的存储长度
/// </summary>
        public T[] data = new T[maxSize];

//头指针
        public int head;

//尾指针
        public int tail;

}
    #endregion

三：常用操作

队列的操作一般分为：

①： 初始化队列。

②:   出队。

③： 入队。

④： 获取队头。

⑤： 获取队长。

1：初始化队列

这个很简单，刚才也说过了，队列是用一个head和tail的指针来维护。分别设置为0即可。

2：出队

看着“队列”的结构图，大家都知道，出队肯定跟head指针有关，需要做两件事情，

第一： 判断队列是否为空，这个我想大家都知道。
       第二： 将head头指针向后移动一位，返回head移动前的元素，时间复杂度为O(1)。

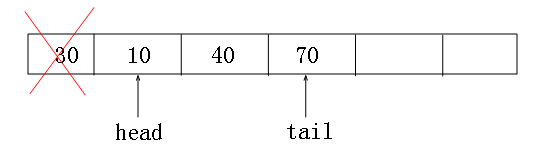
代码段如下：

代码如下:

#region 队列元素出队
        /// <summary>
/// 队列元素出队
/// </summary>
/// <typeparam name="T"></typeparam>
/// <param name="seqQueue"></param>
/// <returns></returns>
        public T SeqQueueOut<T>(SeqQueue<T> seqQueue)
        {
            if (SeqQueueIsEmpty(seqQueue))
                throw new Exception("队列已空，不能进行出队操作");

var single = seqQueue.data[seqQueue.head];

//head指针自增
            seqQueue.data[seqQueue.head++] = default(T);

return single;

}
        #endregion

3：入队

这个跟”出队“的思想相反，同样也是需要做两件事情。

第一：判断队列是否已满。

第二：将tail指针向后移动一位，时间复杂度为O(1)。

代码段如下：

代码如下:

#region 队列元素入队
        /// <summary>
/// 队列元素入队
/// </summary>
/// <typeparam name="T"></typeparam>
/// <param name="seqQueue"></param>
/// <param name="data"></param>
/// <returns></returns>
        public SeqQueue<T> SeqQueueIn<T>(SeqQueue<T> seqQueue, T data)
        {
            //如果队列已满，则不能进行入队操作
            if (SeqQueueIsFull(seqQueue))
                throw new Exception("队列已满,不能入队操作");

//入队操作
            seqQueue.data[seqQueue.tail++] = data;

return seqQueue;
        }
        #endregion

4： 获取队头

知道”出队“和”入队“的原理，相信大家都懂的如何进行”获取队头“操作，唯一不一样的就是

他是只读操作，不会破坏”队列“结构，时间复杂度为O（1）。

代码段如下：

代码如下:

#region 获取队头元素
        /// <summary>
        /// 获取队头元素
        /// </summary>
        /// <typeparam name="T"></typeparam>
        /// <param name="seqQueue"></param>
        /// <returns></returns>
        public T SeqQueuePeek<T>(SeqQueue<T> seqQueue)
        {
            if (SeqQueueIsEmpty(seqQueue))
                throw new Exception("队列已空，不能进行出队操作");

return seqQueue.data[seqQueue.head];
        }
        #endregion

5: 获取队长

大家都知道，我们是用数组来实现队列，所以千万不要想当然的认为数组长度是XXX，

我们维护的是一个head和tail的指针，所以长度自然就是tail-head咯，时间复杂度为O(1)。

代码段如下：

代码如下:

/// <summary>
/// 获取队列长度
/// </summary>
/// <typeparam name="T"></typeparam>
/// <param name="seqQueue"></param>
/// <returns></returns>
        public int SeqQueueLen<T>(SeqQueue<T> seqQueue)
        {
            return seqQueue.tail - seqQueue.head;
        }

然后上一下总的运行代码：

代码如下:

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;

namespace SeqQueue
{
    public class Program
    {
        static void Main(string[] args)
        {
            SeqQueue<Student> seqQueue = new SeqQueue<Student>();

SeqQueueClass queueManage = new SeqQueueClass();

Console.WriteLine("目前队列是否为空：" + queueManage.SeqQueueIsEmpty(seqQueue) + "\n");

Console.WriteLine("将ID=1和ID=2的实体加入队列");
            queueManage.SeqQueueIn(seqQueue, new Student() { ID = 1, Name = "hxc520", Age = 23 });
            queueManage.SeqQueueIn(seqQueue, new Student() { ID = 2, Name = "一线码农", Age = 23 });

Display(seqQueue);

Console.WriteLine("将队头出队");
            //将队头出队
            var student = queueManage.SeqQueueOut(seqQueue);

Display(seqQueue);

//获取队顶元素
            student = queueManage.SeqQueuePeek(seqQueue);

Console.Read();
        }
        //展示队列元素
        static void Display(SeqQueue<Student> seqQueue)
        {
            Console.WriteLine("******************* 链表数据如下 *******************");

for (int i = seqQueue.head; i < seqQueue.tail; i++)
                Console.WriteLine("ID:" + seqQueue.data[i].ID +
                                  ",Name:" + seqQueue.data[i].Name +
                                  ",Age:" + seqQueue.data[i].Age);

Console.WriteLine("******************* 链表数据展示完毕 *******************\n");
        }
    }

#region 学生数据实体
    /// <summary>
/// 学生数据实体
/// </summary>
    public class Student
    {
        public int ID { get; set; }

public string Name { get; set; }

public int Age { get; set; }
    }
    #endregion

#region 队列的数据结构
    /// <summary>
/// 队列的数据结构
/// </summary>
/// <typeparam name="T"></typeparam>
    public class SeqQueue<T>
    {
        private const int maxSize = 100;

public int MaxSize
        {
            get { return maxSize; }
        }

/// <summary>
/// 顺序队列的存储长度
/// </summary>
        public T[] data = new T[maxSize];

//头指针
        public int head;

//尾指针
        public int tail;

}
    #endregion

#region 队列的基本操作
    /// <summary>
/// 队列的基本操作
/// </summary>
    public class SeqQueueClass
    {
        #region 队列的初始化操作
        /// <summary>
/// 队列的初始化操作
/// </summary>
/// <typeparam name="T"></typeparam>
/// <param name="seqQueue"></param>
        public SeqQueue<T> SeqQueueInit<T>(SeqQueue<T> seqQueue)
        {
            seqQueue.head = 0;
            seqQueue.tail = 0;

return seqQueue;
        }
        #endregion

#region 队列是否为空
        /// <summary>
/// 队列是否为空
/// </summary>
/// <typeparam name="T"></typeparam>
/// <param name="seqQueue"></param>
/// <returns></returns>
        public bool SeqQueueIsEmpty<T>(SeqQueue<T> seqQueue)
        {
            //如果两指针重合，说明队列已经清空
            if (seqQueue.head == seqQueue.tail)
                return true;
            return false;
        }
        #endregion

#region 队列是否已满
        /// <summary>
/// 队列是否已满
/// </summary>
/// <typeparam name="T"></typeparam>
/// <param name="seqQueue"></param>
/// <returns></returns>
        public bool SeqQueueIsFull<T>(SeqQueue<T> seqQueue)
        {
            //如果尾指针到达数组末尾，说明队列已经满
            if (seqQueue.tail == seqQueue.MaxSize)
                return true;
            return false;
        }
        #endregion

#region 队列元素入队
        /// <summary>
/// 队列元素入队
/// </summary>
/// <typeparam name="T"></typeparam>
/// <param name="seqQueue"></param>
/// <param name="data"></param>
/// <returns></returns>
        public SeqQueue<T> SeqQueueIn<T>(SeqQueue<T> seqQueue, T data)
        {
            //如果队列已满，则不能进行入队操作
            if (SeqQueueIsFull(seqQueue))
                throw new Exception("队列已满,不能入队操作");

//入队操作
            seqQueue.data[seqQueue.tail++] = data;

return seqQueue;
        }
        #endregion

#region 队列元素出队
        /// <summary>
/// 队列元素出队
/// </summary>
/// <typeparam name="T"></typeparam>
/// <param name="seqQueue"></param>
/// <returns></returns>
        public T SeqQueueOut<T>(SeqQueue<T> seqQueue)
        {
            if (SeqQueueIsEmpty(seqQueue))
                throw new Exception("队列已空，不能进行出队操作");

var single = seqQueue.data[seqQueue.head];

//head指针自增
            seqQueue.data[seqQueue.head++] = default(T);

return single;

}
        #endregion

#region 获取队头元素
        /// <summary>
/// 获取队头元素
/// </summary>
/// <typeparam name="T"></typeparam>
/// <param name="seqQueue"></param>
/// <returns></returns>
        public T SeqQueuePeek<T>(SeqQueue<T> seqQueue)
        {
            if (SeqQueueIsEmpty(seqQueue))
                throw new Exception("队列已空，不能进行出队操作");

return seqQueue.data[seqQueue.head];
        }
        #endregion

/// <summary>
/// 获取队列长度
/// </summary>
/// <typeparam name="T"></typeparam>
/// <param name="seqQueue"></param>
/// <returns></returns>
        public int SeqQueueLen<T>(SeqQueue<T> seqQueue)
        {
            return seqQueue.tail - seqQueue.head;
        }
    }
    #endregion
}

三：顺序队列的缺陷

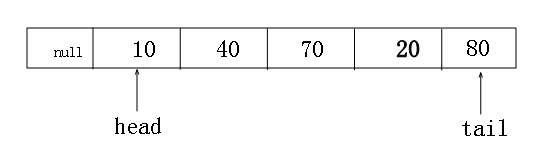
大家看这张图，不知道可有什么异样的感觉，在这种状态下，我入队操作，发现程序提示队列

已满，但是tnd我这个数组还有一个空间啊，是的，这就是所谓的“假溢出”。

四：循环队列

俗话说的好啊，“没有跨不过的坎”。

1: 概念

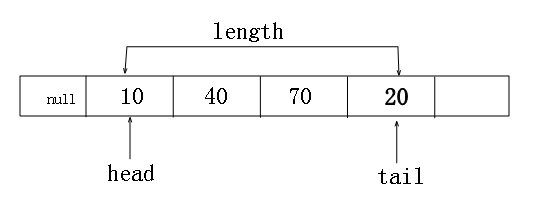
之所以叫“循环”，得益于神奇的“%”。他让队列的首位进行相连，形成了一个我们思维中的

“圈圈”。

2：循环公式

tail=(tail+1)%array.Length;

多看几眼，大家就看通了其中循环的道理，我要做成如下的图:

3：对循环的改造

先前看了一些资料，有的压根就是错的，有的说想要循环，就要牺牲一个单位的空间。

我觉得没必要。我既要循环又不牺牲空间，所以反射了一下framework中的Queue类。

改造后代码如下：

代码如下:

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;

namespace SeqQueue
{
    public class Program
    {
        static void Main(string[] args)
        {
            SeqQueue<Student> seqQueue = new SeqQueue<Student>();

SeqQueueClass queueManage = new SeqQueueClass();

Console.WriteLine("目前队列是否为空：" + queueManage.SeqQueueIsEmpty(seqQueue) + "\n");

Console.WriteLine("将ID=1，2，3的实体加入队列\n");
            queueManage.SeqQueueIn(seqQueue, new Student() { ID = 1, Name = "hxc520", Age = 23 });
            queueManage.SeqQueueIn(seqQueue, new Student() { ID = 2, Name = "一线码农", Age = 23 });
            queueManage.SeqQueueIn(seqQueue, new Student() { ID = 3, Name = "51cto", Age = 23 });

Console.WriteLine("\n当前队列个数：" + queueManage.SeqQueueLen(seqQueue) + "");

Console.WriteLine("\n*********************************************\n");

Console.WriteLine("我要出队了\n");
            queueManage.SeqQueueOut(seqQueue);

Console.WriteLine("哈哈，看看跟顺序队列异样之处，我再入队，看是否溢出\n");
            queueManage.SeqQueueIn(seqQueue, new Student() { ID = 4, Name = "博客园", Age = 23 });
            Console.WriteLine("\n....一切正常，入队成功");

Console.WriteLine("\n当前队列个数：" + queueManage.SeqQueueLen(seqQueue) + "");

Console.Read();
        }
    }

#region 学生数据实体
    /// <summary>
/// 学生数据实体
/// </summary>
    public class Student
    {
        public int ID { get; set; }

public string Name { get; set; }

public int Age { get; set; }
    }
    #endregion

#region 队列的数据结构
    /// <summary>
/// 队列的数据结构
/// </summary>
/// <typeparam name="T"></typeparam>
    public class SeqQueue<T>
    {
        private const int maxSize = 3;

public int MaxSize
        {
            get { return maxSize; }
        }

/// <summary>
/// 顺序队列的存储长度
/// </summary>
        public T[] data = new T[maxSize];

//头指针
        public int head;

//尾指针
        public int tail;

//队列中有效的数字个数
        public int size;
    }
    #endregion

#region 队列的基本操作
    /// <summary>
/// 队列的基本操作
/// </summary>
    public class SeqQueueClass
    {
        #region 队列的初始化操作
        /// <summary>
/// 队列的初始化操作
/// </summary>
/// <typeparam name="T"></typeparam>
/// <param name="seqQueue"></param>
        public SeqQueue<T> SeqQueueInit<T>(SeqQueue<T> seqQueue)
        {
            seqQueue.size = seqQueue.head = seqQueue.tail = 0;

return seqQueue;
        }
        #endregion

#region 队列是否为空
        /// <summary>
/// 队列是否为空
/// </summary>
/// <typeparam name="T"></typeparam>
/// <param name="seqQueue"></param>
/// <returns></returns>
        public bool SeqQueueIsEmpty<T>(SeqQueue<T> seqQueue)
        {
            //如果两指针重合，说明队列已经清空
            if (seqQueue.size == 0)
                return true;
            return false;
        }
        #endregion

#region 队列是否已满
        /// <summary>
/// 队列是否已满
/// </summary>
/// <typeparam name="T"></typeparam>
/// <param name="seqQueue"></param>
/// <returns></returns>
        public bool SeqQueueIsFull<T>(SeqQueue<T> seqQueue)
        {
            //采用循环队列后，头指针
            if (seqQueue.size == seqQueue.MaxSize)
                return true;
            return false;
        }
        #endregion

#region 队列元素入队
        /// <summary>
/// 队列元素入队
/// </summary>
/// <typeparam name="T"></typeparam>
/// <param name="seqQueue"></param>
/// <param name="data"></param>
/// <returns></returns>
        public SeqQueue<T> SeqQueueIn<T>(SeqQueue<T> seqQueue, T data)
        {
            //如果队列已满，则不能进行入队操作
            if (SeqQueueIsFull(seqQueue))
                throw new Exception("队列已满，还入啥队列啊！");

//采用循环队列,必须先赋值，在自增tail指针
            seqQueue.data[seqQueue.tail] = data;
            seqQueue.tail = (seqQueue.tail + 1) % seqQueue.MaxSize;

//队列实际元素增加
            seqQueue.size++;

return seqQueue;
        }
        #endregion

#region 队列元素出队
        /// <summary>
/// 队列元素出队
/// </summary>
/// <typeparam name="T"></typeparam>
/// <param name="seqQueue"></param>
/// <returns></returns>
        public T SeqQueueOut<T>(SeqQueue<T> seqQueue)
        {
            if (SeqQueueIsEmpty(seqQueue))
                throw new Exception("队列已空，大哥，不要在出队了！");

//循环队列出队，展现的是head的灵活性
            seqQueue.head = (seqQueue.head + 1) % seqQueue.MaxSize;

//队列实际元素递减
            seqQueue.size--;

return seqQueue.data[seqQueue.head];
        }
        #endregion

#region 获取队头元素
        /// <summary>
/// 获取队头元素
/// </summary>
/// <typeparam name="T"></typeparam>
/// <param name="seqQueue"></param>
/// <returns></returns>
        public T SeqQueuePeek<T>(SeqQueue<T> seqQueue)
        {
            if (SeqQueueIsEmpty(seqQueue))
                throw new Exception("队列已空，不能进行出队操作");

return seqQueue.data[seqQueue.head];
        }
        #endregion

#region 获取队列长度
        /// <summary>
/// 获取队列长度
/// </summary>
/// <typeparam name="T"></typeparam>
/// <param name="seqQueue"></param>
/// <returns></returns>
        public int SeqQueueLen<T>(SeqQueue<T> seqQueue)
        {
            return seqQueue.size;
        }
        #endregion
    }
    #endregion
}

赞 (0)

相关推荐

  • 算法系列15天速成 第五天 五大经典查找【中】

    算法系列15天速成 第五天 五大经典查找【中】

    哈希查找: 对的,他就是哈希查找,说到哈希,大家肯定要提到哈希函数,呵呵,这东西已经在我们脑子里面形成固有思维了.大家一定要知道"哈希"中的对应关系.     比如说: "5"是一个要保存的数,然后我丢给哈希函数,哈希函数给我返回一个"2",那么此时的"5"和"2"就建立一种对应关系,这种关系就是所谓的"哈希关系",在实际应用中也就形成了"2"是key,"5

  • 算法系列15天速成 第二天 七大经典排序【中】

    算法系列15天速成 第二天 七大经典排序【中】

    首先感谢朋友们对第一篇文章的鼎力支持,感动中.......  今天说的是选择排序,包括"直接选择排序"和"堆排序". 话说上次"冒泡排序"被快排虐了,而且"快排"赢得了内库的重用,众兄弟自然眼红,非要找快排一比高下. 这不今天就来了两兄弟找快排算账. 1.直接选择排序: 先上图: 说实话,直接选择排序最类似于人的本能思想,比如把大小不一的玩具让三岁小毛孩对大小排个序, 那小孩首先会在这么多玩具中找到最小的放在第一位,然后找到次

  • 算法系列15天速成 第一天 七大经典排序【上】

    算法系列15天速成 第一天 七大经典排序【上】

    针对现实中的排序问题,算法有七把利剑可以助你马道成功. 首先排序分为四种:       交换排序: 包括冒泡排序,快速排序.      选择排序: 包括直接选择排序,堆排序.      插入排序: 包括直接插入排序,希尔排序.      合并排序: 合并排序. 那么今天我们讲的就是交换排序,我们都知道,C#类库提供的排序是快排,为了让今天玩的有意思点,我们设计算法来跟类库提供的快排较量较量.争取KO对手. 冒泡排序: 首先我们自己来设计一下"冒泡排序",这种排序很现实的例子就是:我抓一

  • 算法系列15天速成 第十四天 图【上】

    算法系列15天速成 第十四天 图【上】

    今天来分享一下图,这是一种比较复杂的非线性数据结构,之所以复杂是因为他们的数据元素之间的关系是任意的,而不像树那样 被几个性质定理框住了,元素之间的关系还是比较明显的,图的使用范围很广的,比如网络爬虫,求最短路径等等,不过大家也不要胆怯, 越是复杂的东西越能体现我们码农的核心竞争力. 既然要学习图,得要遵守一下图的游戏规则. 一: 概念 图是由"顶点"的集合和"边"的集合组成.记作:G=(V,E): <1> 无向图 就是"图"中的边没

  • 算法系列15天速成——第十三天 树操作【下】

    算法系列15天速成——第十三天 树操作【下】

    听说赫夫曼胜过了他的导师,被认为"青出于蓝而胜于蓝",这句话也是我比较欣赏的,嘻嘻. 一  概念 了解"赫夫曼树"之前,几个必须要知道的专业名词可要熟练记住啊. 1: 结点的权 "权"就相当于"重要度",我们形象的用一个具体的数字来表示,然后通过数字的大小来决定谁重要,谁不重要. 2: 路径 树中从"一个结点"到"另一个结点"之间的分支. 3: 路径长度 一个路径上的分支数量. 4: 树

  • 算法系列15天速成 第三天 七大经典排序【下】

    算法系列15天速成 第三天 七大经典排序【下】

    直接插入排序: 这种排序其实蛮好理解的,很现实的例子就是俺们斗地主,当我们抓到一手乱牌时,我们就要按照大小梳理扑克,30秒后, 扑克梳理完毕,4条3,5条s,哇塞......  回忆一下,俺们当时是怎么梳理的. 最左一张牌是3,第二张牌是5,第三张牌又是3,赶紧插到第一张牌后面去,第四张牌又是3,大喜,赶紧插到第二张后面去, 第五张牌又是3,狂喜,哈哈,一门炮就这样产生了. 怎么样,生活中处处都是算法,早已经融入我们的生活和血液. 下面就上图说明:              看这张图不知道大家可

  • 算法系列15天速成 第四天 五大经典查找【上】

    算法系列15天速成 第四天 五大经典查找【上】

    在我们的算法中,有一种叫做线性查找. 分为:顺序查找.        折半查找. 查找有两种形态: 分为:破坏性查找,   比如有一群mm,我猜她们的年龄,第一位猜到了是23+,此时这位mm已经从我脑海里面的mmlist中remove掉了. 哥不找23+的,所以此种查找破坏了原来的结构. 非破坏性查找, 这种就反之了,不破坏结构. 顺序查找: 这种非常简单,就是过一下数组,一个一个的比,找到为止. 复制代码 代码如下: using System;using System.Collections.

  • 算法系列15天速成 第十一天 树操作（上）

    算法系列15天速成 第十一天 树操作（上）

    先前我们讲的都是"线性结构",他的特征就是"一个节点最多有一个"前驱"和一个"后继".那么我们今天讲的树会是怎样的呢? 我们可以对"线性结构"改造一下,变为"一个节点最多有一个"前驱"和"多个后继".哈哈,这就是我们今天说的"树". 一: 树 我们思维中的"树"就是一种枝繁叶茂的形象,那么数据结构中的"树"该

  • 算法系列15天速成 第六天 五大经典查找【下】

    算法系列15天速成 第六天 五大经典查找【下】

    大家是否感觉到,树在数据结构中大行其道,什么领域都要沾一沾,碰一碰.就拿我们前几天学过的排序就用到了堆和今天讲的"二叉排序树",所以偏激的说,掌握的树你就是牛人了. 今天就聊聊这个"五大经典查找"中的最后一个"二叉排序树". 1. 概念:     <1> 其实很简单,若根节点有左子树,则左子树的所有节点都比根节点小.                             若根节点有右子树,则右子树的所有节点都比根节点大.     &

  • 算法系列15天速成 第十二天 树操作【中】

    算法系列15天速成 第十二天 树操作【中】

    先前说了树的基本操作,我们采用的是二叉链表来保存树形结构,当然二叉有二叉的困扰之处,比如我想找到当前结点的"前驱"和"后继",那么我们就必须要遍历一下树,然后才能定位到该"节点"的"前驱"和"后继",每次定位都是O(n),这不是我们想看到的,那么有什么办法来解决呢? (1) 在节点域中增加二个指针域,分别保存"前驱"和"后继",那么就是四叉链表了,哈哈,还是有点浪费空

  • 算法系列15天速成——第十五天 图【下】（大结局）

    算法系列15天速成——第十五天 图【下】（大结局）

    今天是大结局,说下"图"的最后一点东西,"最小生成树"和"最短路径". 一: 最小生成树 1. 概念 首先看如下图,不知道大家能总结点什么. 对于一个连通图G,如果其全部顶点和一部分边构成一个子图G1,当G1满足: ① 刚好将图中所有顶点连通.②顶点不存在回路.则称G1就是G的"生成树". 其实一句话总结就是:生成树是将原图的全部顶点以最小的边连通的子图,这不,如下的连通图可以得到下面的两个生成树. ② 对于一个带权的连通图,

  • 算法系列15天速成 第八天 线性表【下】

    算法系列15天速成 第八天 线性表【下】

    一:线性表的简单回顾 上一篇跟大家聊过"线性表"顺序存储,通过实验,大家也知道,如果我每次向顺序表的头部插入元素,都会引起痉挛,效率比较低下,第二点我们用顺序存储时,容易受到长度的限制,反之就会造成空间资源的浪费. 二:链表 对于顺序表存在的若干问题,链表都给出了相应的解决方案. 1. 概念:其实链表的"每个节点"都包含一个"数据域"和"指针域". "数据域"中包含当前的数据. "指针域"

  • 算法系列15天速成 第十天 栈

    算法系列15天速成 第十天 栈

    一: 概念 栈,同样是一种特殊的线性表,是一种Last In First Out(LIFO)的形式,现实中有很多这样的例子, 比如:食堂中的一叠盘子,我们只能从顶端一个一个的取. 二:存储结构 "栈"不像"队列",需要两个指针来维护,栈只需要一个指针就够了,这得益于栈是一种一端受限的线性表. 这里同样用"顺序结构"来存储这个"栈",top指针指向栈顶,所有的操作只能在top处. 代码段: 复制代码 代码如下: #region

  • 算法系列15天速成 第七天 线性表【上】

    算法系列15天速成 第七天 线性表【上】

    哈哈,我们的数据也一样,存在这三种基本关系,用术语来说就是: <1>  线性关系.<2>  树形关系.<3>  网状关系. 一: 线性表 1 概念:                 线性表也就是关系户中最简单的一种关系,一对一.                  如:学生学号的集合就是一个线性表. 2 特征:                 ① 有且只有一个"首元素".                 ② 有且只有一个"末元素".

随机推荐