TypeScript数据结构链表结构 LinkedList教程及面试

目录

• 1. 认识链表
• 2. 实现链表结构的封装
• 2.1 基础框架 v1 版
• 2.2 添加 append 方法 v2 版
• 2.3 添加 traverse 方法 v3 版
• 2.4 添加 insert 方法 v4 版
• 2.5 添加 removeAt 方法 v5 版
• 2.6 添加 get 方法 v6 版
• 2.7 添加 getNode 方法 v7 版
• 2.8 添加 update 方法 v8 版
• 2.9 添加 indexOf 方法 v9 版
• 2.10 添加 remove 方法 v10 版
• 2.11 添加方法 isEmpty v11 版
• 3. 面试题一：设计链表
• 3.1 题目描述
• 3.2 解答
• 4. 面试题二：删除链表中的节点
• 4.1 题目描述
• 4.2 解答
• 5. 面试题三：反转链表
• 5.1 解一：栈结构
• 5.2 解二：迭代
• 5.3 解三：递归

1. 认识链表

• 链表是一种通过指针的形式把一组存储单元联系在一起的数据结构。
• js 中没有链表，但可以用 Object 模拟链表
• 链表类似于火车：有一个火车头，火车头会连接一个节点，节点上有乘客（类似于数据），并且这个节点会连接下一个节点，以此类推

链表的火车结构：

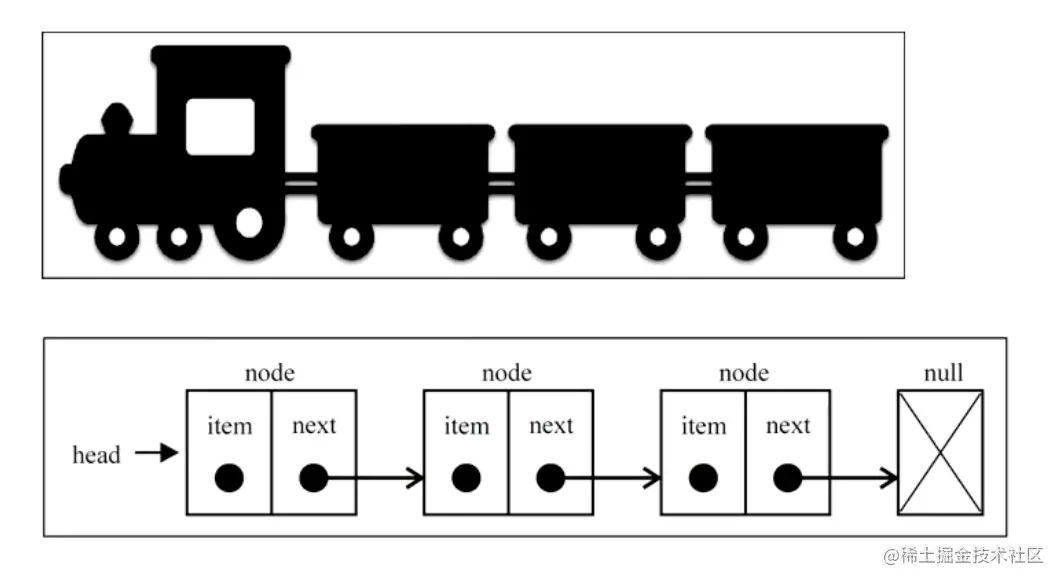
链表的常见操作：

append(element)：向链表尾部添加一个新的项

insert(value, position)：向链表的特定位置插入一个新的项

get(position)：获取对应位置的元素

indexOf(element)：返回元素在链表中的索引。如果链表中没有该元素则返回 -1

update(position,element)：修改某个位置的元素

removeAt(postion)：从链表的特定位置移除一项

remove(element)：从链表中移除一项

isEmpty()：如果链表中不包含任何元素，返回 true，如果链表长度大于等于0返回false

size()：返回链表包含的元素个数。与数组的length属性类似

2. 实现链表结构的封装

2.1 基础框架 v1 版

// 1. 创建 Node 节点类
class Node<T> {
  value: T;
  next: Node<T> | null = null;
  constructor(value: T) {
    this.value = value;
  }
}
// 2. 创建 LinkedList 的类
class LinkedList<T> {
  private head: Node<T> | null = null;
  private size: number = 0;
  get length() {
    return this.size;
  }
}

代码解析：

• 封装一个 Node 类，用于封装每一个节点上的信息（包括和指向下一个节点的引用），它是一个泛型类
• 封装一个 LinkedList 类，用于表示链表结构
• 链表中保存两个属性，
  
  size：链表长度

  head：链表中的第一个节点

基础的框架搭建好了，我们接下来就来一个个添加方法

2.2 添加 append 方法 v2 版

向 LinkedList 添加 append(element) 方法

append 方法的作用是向链表尾部添加一个新的项

  append(value: T) {
    // 1. 根据 value创建一个新节点
    const newNode = new Node(value)
    // 2. 判断 this.head 是否为 null
    if(!this.head) {
      this.head = newNode
    } else {
      let current = this.head
      while(current.next) {
        current = current.next
      }
      // 此时 current 指向最后一个节点
      current.next = newNode
    }
    // 3. size++
    this.size++
  }

2.3 添加 traverse 方法 v3 版

为了方便可以看到链表上的每一个节点，我们实现一个 traverse 方法

向 LinkedList 添加 traverse 方法

traverse 方法的作用是 遍历链表

  traverse() {
    const values: T[] = [];
    let current = this.head;
    while (current) {
      values.push(current.value);
      current = current.next;
    }
    console.log(values.join("->"));
  }

测试：

const l = new LinkedList<string>();
l.append("第一个节点");
l.append("第二个节点");
l.append("第三个节点");
l.traverse();  // 第一个节点->第二个节点->第三个节点

2.4 添加 insert 方法 v4 版

向 LinkedList 添加 insert(value, position) 方法

insert方法的作用是向链表的特定位置插入一个新的项

  insert(value: T, position: number): boolean {
    // 1. 越界判断
    if (position < 0 || position >= this.size) return false;
    // 2. 根据 value 创建新的节点
    const newNode = new Node(value);
    // 3. 判断是否需要插入头部
    if (position === 0) {
      newNode.next = this.head;
      this.head = newNode;
    } else {
      let current = this.head;
      let previous: Node<T> | null = null;
      let index = 0;
      while (index++ < position && current) {
        previous = current;
        current = current.next;
      }
      // index === position
      newNode.next = current;
      previous!.next = newNode;
    }
    return true;
  }

测试：

const l = new LinkedList<string>();
l.append("aaa");
l.append("bbb");
l.append("ccc");
// l.insert("ddd", 0); // 插入头部位置 ddd->aaa->bbb->ccc
// l.insert("ddd", 2); // 插入第二个位置  aaa->bbb->ddd->ccc
// l.insert("ddd", 3); // 插入尾部 aaa->bbb->ccc->ddd
l.traverse();

2.5 添加 removeAt 方法 v5 版

向 LinkedList 添加 removeAt(postion) 方法

removeAt方法的作用是从链表的特定位置移除一项

  removeAt(position: number): T | null {
    // 1. 越界判断
    if (position < 0 || position > this.size) return null;
    // 2. 判断是否删除第一个节点
    let current = this.head;
    if (position === 0) {
      this.head = current?.next ?? null;
    } else {
      let previous: Node<T> | null = null;
      let index = 0;
      while (index++ < position && current) {
        previous = current;
        current = current.next;
      }
      previous!.next = current?.next ?? null;
    }
    this.size--;
    return current?.value ?? null;
  }

测试：

const l = new LinkedList<string>();
l.append("aaa");
l.append("bbb");
l.append("ccc");
// console.log(l.removeAt(0)); // aaa
// console.log(l.removeAt(1)); // bbb
// console.log(l.removeAt(2)); // ccc
// console.log(l.removeAt(3)); // null
l.traverse();

2.6 添加 get 方法 v6 版

向 LinkedList 添加 get(postion) 方法

get方法的作用是获取对应位置的元素

  get(position: number): T | null {
    // 越界问题
    if (position < 0 || position >= this.size) return null;
    // 2. 查找元素
    let index = 0;
    let current = this.head;
    while (index++ < position && current) {
      current = current?.next;
    }
    // index === position
    return current?.value ?? null;
  }

测试：

const l = new LinkedList<string>();
l.append("aaa");
l.append("bbb");
l.append("ccc");
console.log(l.get(0)); // aaa
console.log(l.get(1)); // bbb
console.log(l.get(2)); // ccc
console.log(l.get(3)); // null

2.7 添加 getNode 方法 v7 版

到这里，我们发现上面的代码在 通过 position 获取节点的逻辑 上有很多重复的地方，现在我们通过添加 getNode 方法来重构一下

向 LinkedList 添加 getNode(postion) 私有方法

getNode方法的作用是获取对应位置的节点

  // 封装私有方法
  // 根据 position 获取得到当前的节点
  private getNode(position: number): Node<T> | null {
    let index = 0;
    let current = this.head;
    while (index++ < position && current) {
      current = current?.next;
    }
    return current;
  }

有了这个方法，我们就可以对 get removeAt insert 方法进行重构了

• 对 removeAt 进行重构

  removeAt(position: number): T | null {
    // 1. 越界判断
    if (position < 0 || position > this.size) return null;
    // 2. 判断是否删除第一个节点
    let current = this.head;
    if (position === 0) {
      this.head = current?.next ?? null;
    } else {
-      let previous: Node<T> | null = null;
-      let index = 0;
-
-      while (index++ < position && current) {
-        previous = current;
-        current = current.next;
-      }
-      previous!.next = current?.next ?? null;
+      let previous = this.getNode(position - 1);
+      current = previous?.next ?? null;
+      previous!.next = previous?.next?.next ?? null;
    }
    this.size--;
    return current?.value ?? null;
  }

• 对 get 进行重构

  get(position: number): T | null {
    // 越界问题
    if (position < 0 || position >= this.size) return null;
    // 2. 查找元素
-    let index = 0;
-    let current = this.head;
-    while (index++ < position && current) {
-      current = current?.next;
-    }
+    let current = this.getNode(position);
    return current?.value ?? null;
  }

• 对 insert 进行重构

  insert(value: T, position: number): boolean {
    // 1. 越界判断
    if (position < 0 || position > this.size) return false;
    // 2. 根据 value 创建新的节点
    const newNode = new Node(value);
    // 3. 判断是否需要插入头部
    if (position === 0) {
      newNode.next = this.head;
      this.head = newNode;
    } else {
-      let current = this.head;
-      let previous: Node<T> | null = null;
-      let index = 0;
-
-      while (index++ < position && current) {
-        previous = current;
-        current = current.next;
-      }
-
-      // index === position
-      newNode.next = current;
-      previous!.next = newNode;
+      const previous = this.getNode(position - 1);
+      newNode.next = previous?.next ?? null;
+      previous!.next = newNode;
    }
    return true;
  }

测试一把，都没问题

const l = new LinkedList<string>();
l.append("aaa");
l.append("bbb");
l.append("ccc");
// console.log(l.removeAt(0)); // aaa
// console.log(l.removeAt(1)); // bbb
// console.log(l.removeAt(2)); // ccc
// console.log(l.removeAt(3)); // null
// console.log(l.get(0)) // aaa
// console.log(l.get(1)) // bbb
// console.log(l.get(2)) // ccc
// console.log(l.get(3)) // null
// l.insert("ddd", 0); // ddd->aaa->bbb->ccc
// l.insert("ddd", 1); // aaa->ddd->bbb->ccc
// l.insert("ddd", 2); // aaa->bbb->ddd->ccc
// l.insert("ddd", 3); // aaa->bbb->ccc->ddd
// l.insert("ddd", 4); // aaa->bbb->ccc
l.traverse();

2.8 添加 update 方法 v8 版

向 LinkedList 添加 update(position,element) 方法

update方法的作用是修改某个位置的元素

  update(value: T, position: number):boolean {
    if (position < 0 || position >= this.size) return false;
    // 获取对应位置的节点，直接更新即可
    const currentNode = this.getNode(position)
    currentNode!.value = value
    return true
  }

测试：

const l = new LinkedList<string>();
l.append("aaa");
l.append("bbb");
l.append("ccc");
l.traverse(); // aaa->bbb->ccc
l.update("ddd", 1); // aaa->ddd->ccc
l.traverse();

2.9 添加 indexOf 方法 v9 版

向 LinkedList 添加 indexOf(element) 方法

indexOf方法的作用是返回元素在链表中的索引。如果链表中没有该元素则返回 -1

  indexOf(value: T) {
    // 从第一个节点开始，向后遍历
    let current = this.head;
    let index = 0;
    while (current) {
      if (current.value === value) {
        return index;
      }
      current = current.next;
      index++;
    }
    return -1;
  }

测试：

const l = new LinkedList<string>();
l.append("aaa");
l.append("bbb");
l.append("ccc");
console.log(l.indexOf("aaa"));
console.log(l.indexOf("bbb"));
console.log(l.indexOf("ccc"));

2.10 添加 remove 方法 v10 版

向 LinkedList 添加 remove(element) 方法

remove方法的作用是从链表中移除一项

  remove(value: T): T | null {
    const index = this.indexOf(value);
    return this.removeAt(index);
  }

测试：

const l = new LinkedList<string>();
l.append("aaa");
l.append("bbb");
l.append("ccc");
l.remove('bbb')
l.traverse() // aaa->ccc

2.11 添加方法 isEmpty v11 版

向 LinkedList 添加 isEmpty() 方法

isEmpty方法的作用是如果链表中不包含任何元素，返回 true，如果链表长度大于等于 0 返回 false

  isEmpty(): boolean {
    return this.size === 0;
  }

3. 面试题一：设计链表

这是 Leetcode 上的第 707 道题，难度为：中等

3.1 题目描述

设计链表的实现。您可以选择使用单链表或双链表。单链表中的节点应该具有两个属性：val 和 next。val 是当前节点的值，next 是指向下一个节点的指针/引用。如果要使用双向链表，则还需要一个属性 prev 以指示链表中的上一个节点。假设链表中的所有节点都是 0-index 的。

在链表类中实现这些功能：

• get(index)：获取链表中第 index 个节点的值。如果索引无效，则返回-1。
• addAtHead(val)：在链表的第一个元素之前添加一个值为 val 的节点。插入后，新节点将成为链表的第一个节点。
• addAtTail(val)：将值为 val 的节点追加到链表的最后一个元素。
• addAtIndex(index,val)：在链表中的第 index 个节点之前添加值为 val  的节点。如果 index 等于链表的长度，则该节点将附加到链表的末尾。如果 index 大于链表长度，则不会插入节点。如果index小于0，则在头部插入节点。
• deleteAtIndex(index)：如果索引 index 有效，则删除链表中的第 index 个节点。

示例：

MyLinkedList linkedList = new MyLinkedList();
linkedList.addAtHead(1);
linkedList.addAtTail(3);
linkedList.addAtIndex(1,2);   //链表变为1-> 2-> 3
linkedList.get(1);            //返回2
linkedList.deleteAtIndex(1);  //现在链表是1-> 3
linkedList.get(1);            //返回3

提示：

• 0 <= index, val <= 1000
• 请不要使用内置的 LinkedList 库。
• get, addAtHead, addAtTail, addAtIndex 和 deleteAtIndex 的操作次数不超过 2000。

3.2 解答

这道题的答案在第二章就已经给出了，我们只需要进行一些修改即可

class Node {
  value: number;
  next: Node | null = null;
  constructor(value: number) {
    this.value = value;
  }
}
class MyLinkedList {
  private head: Node | null = null;
  private size: number = 0;
  constructor() {}
  private getNode(position: number): Node | null {
    let index = 0;
    let current = this.head;
    while (index++ < position && current) {
      current = current?.next;
    }
    return current;
  }
  get(index: number): number {
    if (index < 0 || index >= this.size) return -1;
    let current = this.getNode(index);
    return current!.value;
  }
  addAtHead(val: number): void {
    const newNode = new Node(val);
    if (!this.head) {
      this.head = newNode;
    } else {
      newNode.next = this.head;
      this.head = newNode;
    }
    this.size++;
  }
  addAtTail(val: number): void {
    const newNode = new Node(val);
    if (!this.head) {
      this.head = newNode;
    } else {
      let current = this.getNode(this.size - 1);
      current!.next = newNode;
    }
    this.size++;
  }
  addAtIndex(index: number, val: number): void {
    if (index > this.size) return;
    if (index <= 0) {
      this.addAtHead(val);
    } else {
      const newNode = new Node(val);
      const previous = this.getNode(index - 1);
      newNode.next = previous?.next ?? null;
      previous!.next = newNode;
    }
    this.size++;
  }
  deleteAtIndex(index: number): void {
    if (index < 0 || index >= this.size) return;
    let current = this.head;
    if (index === 0) {
      this.head = current?.next ?? null;
    } else {
      const previous = this.getNode(index - 1);
      previous!.next = previous?.next?.next ?? null;
    }
    this.size--;
  }
}

复杂度分析：

时间复杂度：

初始化消耗 O(1)

get 消耗 O(index)

addAtHead 消耗 O(1)

addAtTail 消耗 O(n)，其中 n 为链表当前长度

addAtIndex 消耗 O(index)

deleteAtIndex 消耗 O(index - 1)

• 空间复杂度：所有函数的单词调用空间复杂度均为 O(1)，总体空间复杂度为 O(n)，

4. 面试题二：删除链表中的节点

这是 Leetcode 上的第 237 道题，难度为：中等

4.1 题目描述

有一个单链表的 head，我们想删除它其中的一个节点 node。

给你一个需要删除的节点 node 。你将 无法访问 第一个节点  head。

链表的所有值都是 唯一的，并且保证给定的节点 node 不是链表中的最后一个节点。

删除给定的节点。注意，删除节点并不是指从内存中删除它。这里的意思是：

• 给定节点的值不应该存在于链表中。
• 链表中的节点数应该减少 1。
• node 前面的所有值顺序相同。
• node 后面的所有值顺序相同。

自定义测试：

• 对于输入，你应该提供整个链表 head 和要给出的节点 node。node 不应该是链表的最后一个节点，而应该是链表中的一个实际节点。
• 我们将构建链表，并将节点传递给你的函数。
• 输出将是调用你函数后的整个链表。

示例 1：

输入： head = [4,5,1,9], node = 5
输出： [4,1,9]
解释： 指定链表中值为 5 的第二个节点，那么在调用了你的函数之后，该链表应变为 4 -> 1 -> 9

示例 2：

输入： head = [4,5,1,9], node = 1
输出： [4,5,9]
解释： 指定链表中值为 1 的第三个节点，那么在调用了你的函数之后，该链表应变为 4 -> 5 -> 9

提示：

• 链表中节点的数目范围是 [2, 1000]
• -1000 <= Node.val <= 1000
• 链表中每个节点的值都是 唯一 的
• 需要删除的节点 node 是 链表中的节点 ，且 不是末尾节点

4.2 解答

删除节点的操作我们其实之前就已经实现了的，我们只要拿到要删除节点的前一个节点，将前一个节点的 next 指向要删除节点的下一个节点即可。 但是这道题有一个问题就是，我们拿不到要删除前点的上一个节点。

思路：

我们可以将要删除的节点的值赋值成它的下一个节点就行了，这样就将问题从删除某个节点转换成了删除某个节点的后一个节点，这样的好处就是我们能拿到要删除节点的前一个节点。

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     val: number
 *     next: ListNode | null
 *     constructor(val?: number, next?: ListNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.next = (next===undefined ? null : next)
 *     }
 * }
 */
/**
 Do not return anything, modify it in-place instead.
 */
function deleteNode(node: ListNode | null): void {
  node.val = node.next.val;
  node.next = node.next.next;
}

复杂度分析

• 时间复杂度：O(1)。
• 空间复杂度：O(1)。

5. 面试题三：反转链表

这是 Leetcode 上的第 206 道题，难度为：中等

5.1 解一：栈结构

这道题可以用栈来解决，利用栈的 后进先出 的特性。

思路：先依次将数据 push 进栈中，再一次从栈中 pop 出数据，拼接 pop 出来的元素成一个新的链表。

function reverseList(head: ListNode | null): ListNode | null {
  // head 本身为 null 时 不需要处理
  if (head === null) return null;
  // 只有一个节点
  if (!head.next) return head;
  // 数组模拟栈结构
  const stack: ListNode[] = [];
  let current: ListNode | null = head;
  while (current) {
    stack.push(current);
    current = current.next;
  }
  // 依次从栈结构中取出元素，放到一个新的链表中
  const newHead: ListNode = stack.pop()!
  let newHeadCurrent = newHead
  while(stack.length) {
    const node = stack.pop()!
    newHeadCurrent.next = node
    newHeadCurrent = newHeadCurrent.next
  }
  newHeadCurrent.next = null
  return newHead
}

复杂度分析：

• 时间复杂度：O(2n) ，n 为链表的长度，因为要遍历两次链表
• 空间复杂度：O(n)，额外需要使用栈这种结构

5.2 解二：迭代

假设链表为 1 ️ 2 ️ 3 ️ 4 ️ ∅，我们想要把它改成 ∅ ️ 1 ️ 2 ️ 3 ️ 4

思路：在遍历链表时，将当前节点的 next 指针改为指向前一个节点。由于节点没有引用其前一个节点，因此必须事先存储其前一个节点。在更改引用之前，还需要存储后一个节点。最后返回新的头引用。

function reverseList(head: ListNode | null): ListNode | null {
  // 1. 判断节点为 null，或者只要一个节点，那么直接返回即可
  if (head === null || head.next === null) return head;
  // 2. 反转链表结构
  let newHead: ListNode | null = null
  while(head) {
    const current: ListNode | null = head.next
    head.next = newHead
    newHead = head
    head = current
  }
  return newHead
}

复杂度分析

• 时间复杂度：O(n)，其中 n 是链表的长度。需要遍历链表一次。
• 空间复杂度：O(1)。

5.3 解三：递归

递归版本稍微复杂一些，其关键在于反向工作。

思路：

假如我们有一个链表 1 -> 2 -> 3 -> 4

如果我们想反转 1 <- 2 就必须先将反转 2 <- 3，因为如果我们将 1 -> 2 反转成 1 <- 2 后，那么 2 后边的节点就再也拿不到了。按照上面的逻辑递归，我们需要先将最后的 3 -> 4 反转成 3 <- 4 在反转前面的节点。

function reverseList(head: ListNode | null): ListNode | null {
  // 1. 判断节点为 null，或者只要一个节点，那么直接返回即可
  if (head === null || head.next === null) {
    return head
  };
  const newHead = reverseList(head.next);
  head.next.next = head;
  head.next = null;
  return newHead;
}

复杂度分析：

• 时间复杂度：O(n)，其中 n 是链表的长度。需要对链表的每个节点进行反转操作。
• 空间复杂度：O(n)，其中 n 是链表的长度。空间复杂度主要取决于递归调用的栈空间，最多为 n 层。

以上就是TypeScript数据结构链表结构 LinkedList教程及面试的详细内容，更多关于TypeScript 链表结构的资料请关注我们其它相关文章！