python之拟合的实现

一、多项式拟合

多项式拟合的话，用的的是numpy这个库的polyfit这个函数。那么多项式拟合，最简单的当然是，一次多项式拟合了，就是线性回归。直接看代码吧

import numpy as np

def linear_regression(x,y):
 #y=bx+a，线性回归
 num=len(x)
 b=(np.sum(x*y)-num*np.mean(x)*np.mean(y))/(np.sum(x*x)-num*np.mean(x)**2)
 a=np.mean(y)-b*np.mean(x)
 return np.array([b,a])
def f(x):
 return 2*x+1
x=np.linspace(-5,5)
y=f(x)+np.random.randn(len(x))#加入噪音
y_fit=np.polyfit(x,y,1)#一次多项式拟合，也就是线性回归
print(linear_regression(x,y))
print(y_fit)

手写线性回归我还是会的，然后我们来看下输出：

[1.9937839 1.24167225]
[1.9937839 1.24167225]

由于有random每次显示的结果都不一样，但很明显的是上下两个print是意料之中的一样，emmmmm，一次多项式拟合的源代码应该就是像我写的那样。好了，那么一次以上呢？咳咳，我数学不算太好，还是老老实实用库函数吧，顺便画下图，见识它的威力。

import numpy as np
from matplotlib import pyplot as plt

def f(x):
 return x**2+1
def f_fit(x,y_fit):
 a,b,c=y_fit.tolist()
 return a*x**2+b*x+c
x=np.linspace(-5,5)
y=f(x)+np.random.randn(len(x))#加入噪音
y_fit=np.polyfit(x,y,2)#二次多项式拟合
y_show=np.poly1d(y_fit)#函数优美的形式
print(y_show)#打印
y1=f_fit(x,y_fit)
plt.plot(x,f(x),'r',label='original')
plt.scatter(x,y,c='g',label='before_fitting')#散点图
plt.plot(x,y1,'b--',label='fitting')
plt.title('polyfitting')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()#显示标签
plt.show()

输出：

2
1.001 x - 0.04002 x + 0.8952

拟合效果看起来还是不错的。

二、各种函数的拟合

一般来说，多项式的拟合就能拟合很多函数了，比如指数函数，取对数就能化为多项式函数，甚至是一次多项式函数。可是，那些三角函数之类的复杂函数不能化为多项式去拟合，怎么办呢？要用到scipy.optimize的curve_fit函数了。

直接贴代码：

import numpy as np
from matplotlib import pyplot as plt
from scipy.optimize import curve_fit

def f(x):
 return 2*np.sin(x)+3
def f_fit(x,a,b):
 return a*np.sin(x)+b
def f_show(x,p_fit):
 a,b=p_fit.tolist()
 return a*np.sin(x)+b
x=np.linspace(-2*np.pi,2*np.pi)
y=f(x)+0.5*np.random.randn(len(x))#加入了噪音
p_fit,pcov=curve_fit(f_fit,x,y)#曲线拟合
print(p_fit)#最优参数
print(pcov)#最优参数的协方差估计矩阵
y1=f_show(x,p_fit)
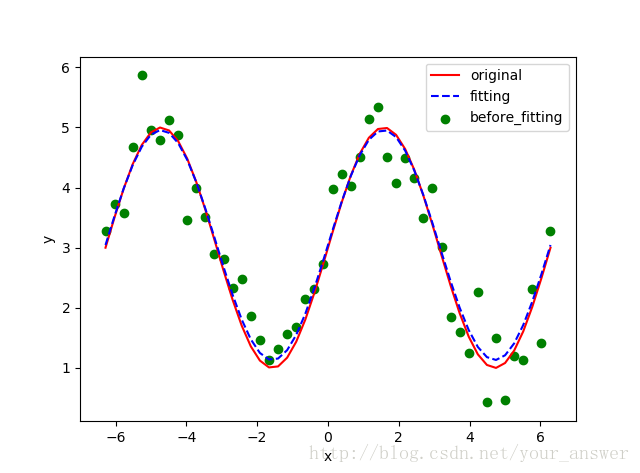
plt.plot(x,f(x),'r',label='original')
plt.scatter(x,y,c='g',label='before_fitting')#散点图
plt.plot(x,y1,'b--',label='fitting')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()

输出：

[1.91267059 3.04489528]
[[ 9.06910892e-03 -1.83703696e-11]
[-1.83703696e-11 4.44386331e-03]]

使用方法基础的就是这样了。然后更多详细的参数的使用就是要看官网了。

1、https://docs.scipy.org/doc/numpy/reference/generated/numpy.polyfit.html

2、https://docs.scipy.org/doc/scipy-0.18.1/reference/generated/scipy.optimize.curve_fit.html

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持我们。

赞 (0)

相关推荐

  • Python实现二维曲线拟合的方法

    如下所示: from numpy import * import numpy as np import matplotlib.pyplot as plt plt.close() fig=plt.figure() plt.grid(True) plt.axis([0,10,0,8]) #列出数据 point=[[1,2],[2,3],[3,6],[4,7],[6,5],[7,3],[8,2]] plt.xlabel("X") plt.ylabel("Y") #用于求出

  • python中matplotlib实现最小二乘法拟合的过程详解

    python中matplotlib实现最小二乘法拟合的过程详解

    前言 最小二乘法Least Square Method,做为分类回归算法的基础,有着悠久的历史(由马里·勒让德于1806年提出).它通过最小化误差的平方和寻找数据的最佳函数匹配.利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小.最小二乘法还可用于曲线拟合.其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达. 下面这篇文章主要跟大家介绍了关于python中matplotlib实现最小二乘法拟合的相关内容,下面话不多说,来一起看看详细的介绍:

  • python实现三维拟合的方法

    如下所示: from matplotlib import pyplot as plt import numpy as np from mpl_toolkits.mplot3d import Axes3D fig = plt.figure() ax = Axes3D(fig) #列出实验数据 point=[[2,3,48],[4,5,50],[5,7,51],[8,9,55],[9,12,56]] plt.xlabel("X1") plt.ylabel("X2") #

  • Python 做曲线拟合和求积分的方法

    这是一个由加油站油罐传感器测量的油罐高度数据和出油体积,根据体积和高度的倒数,用截面积来描述油罐形状,求出拟合曲线,再用标准数据,求积分来验证拟合曲线效果和误差的一个小项目. 主要的就是首先要安装Anaconda  python库,然后来运用这些数学工具. ###最小二乘法试验### import numpy as np import pymysql from scipy.optimize import leastsq from scipy import integrate ###绘图,看拟合效

  • Python实现曲线拟合操作示例【基于numpy,scipy,matplotlib库】

    Python实现曲线拟合操作示例【基于numpy,scipy,matplotlib库】

    本文实例讲述了Python实现曲线拟合操作.分享给大家供大家参考,具体如下: 这两天学习了用python来拟合曲线. 一.环境配置 本人比较比较懒,所以下载的全部是exe文件来安装,安装按照顺利来安装.自动会找到python的安装路径,一直点下一步就行.还有其他的两种安装方式:一种是解压,一种是pip.我没有尝试,就不乱说八道了. 没有ArcGIS 环境的,可以不看下面这段话了. 在配置环境时遇见一个小波折,就是原先电脑装过ArcGIS10.2 ,所以其会默认安装python2.7,而且pyth

  • Python实现的多项式拟合功能示例【基于matplotlib】

    Python实现的多项式拟合功能示例【基于matplotlib】

    本文实例讲述了Python实现的多项式拟合功能.分享给大家供大家参考,具体如下: # -*- coding: utf-8 -*- #! python2 import numpy as np import matplotlib.pyplot as plt from pylab import mpl mpl.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体 plt.rcParams['axes.unicode_minus']=False #解决负数坐

  • Python 确定多项式拟合/回归的阶数实例

    通过 1至10 阶来拟合对比 均方误差及R评分,可以确定最优的"最大阶数". import numpy as np import matplotlib.pyplot as plt from sklearn.preprocessing import PolynomialFeatures from sklearn.linear_model import LinearRegression,Perceptron from sklearn.metrics import mean_squared_

  • Python基于最小二乘法实现曲线拟合示例

    Python基于最小二乘法实现曲线拟合示例

    本文实例讲述了Python基于最小二乘法实现曲线拟合.分享给大家供大家参考,具体如下: 这里不手动实现最小二乘,调用scipy库中实现好的相关优化函数. 考虑如下的含有4个参数的函数式: 构造数据 import numpy as np from scipy import optimize import matplotlib.pyplot as plt def logistic4(x, A, B, C, D): return (A-D)/(1+(x/C)**B)+D def residuals(p

  • Python数据拟合与广义线性回归算法学习

    Python数据拟合与广义线性回归算法学习

    机器学习中的预测问题通常分为2类:回归与分类. 简单的说回归就是预测数值,而分类是给数据打上标签归类. 本文讲述如何用Python进行基本的数据拟合,以及如何对拟合结果的误差进行分析. 本例中使用一个2次函数加上随机的扰动来生成500个点,然后尝试用1.2.100次方的多项式对该数据进行拟合. 拟合的目的是使得根据训练数据能够拟合出一个多项式函数,这个函数能够很好的拟合现有数据,并且能对未知的数据进行预测. 代码如下: import matplotlib.pyplot as plt import

  • python matplotlib拟合直线的实现

    python matplotlib拟合直线的实现

    这篇文章主要介绍了python matplotlib拟合直线的实现,文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习价值,需要的朋友可以参考下 代码如下 import numpy as np import matplotlib.pyplot as plt plt.rcParams['font.family'] = ['sans-serif'] plt.rcParams['font.sans-serif'] = ['SimHei'] def linear_regression

  • Python线性拟合实现函数与用法示例

    Python线性拟合实现函数与用法示例

    本文实例讲述了Python线性拟合实现函数与用法.分享给大家供大家参考,具体如下: 1. 参考别人写的: #-*- coding:utf-8 -*- import math import matplotlib.pyplot as plt def linefit(x , y): N = float(len(x)) sx,sy,sxx,syy,sxy=0,0,0,0,0 for i in range(0,int(N)): sx += x[i] sy += y[i] sxx += x[i]*x[i]

  • python多项式拟合之np.polyfit 和 np.polyld详解

    python数据拟合主要可采用numpy库,库的安装可直接用pip install numpy等. 1. 原始数据:假如要拟合的数据yyy来自sin函数,np.sin import numpy as np import matplotlib.pyplot as plt xxx = np.arange(0, 1000) # x值,此时表示弧度 yyy = np.sin(xxx*np.pi/180) #函数值,转化成度 2. 测试不同阶的多项式,例如7阶多项式拟合,使用np.polyfit拟合,np

  • Python数据拟合实现最小二乘法示例解析

    Python数据拟合实现最小二乘法示例解析

    目录 线性拟合 高阶多项式 多自变量 指数函数 所谓最小二乘法,即通过对数据进行拟合,使得拟合值与样本值的方差最小. 线性拟合 这个表达式还是非常简单的. 对于有些情况,我们往往选取自然序列作为自变量,这个时候在求自变量的取值时可以用到一些初等数学的推论,对于 x ∈ [ m , n ] 的自然序列来说,有 #文件名core.py import numpy as np def leastSquare(x,y): if len(x)==2: #此时x为自然序列 sx = 0.5*(x[1]-x[0

  • python之拟合的实现

    一.多项式拟合 多项式拟合的话,用的的是numpy这个库的polyfit这个函数.那么多项式拟合,最简单的当然是,一次多项式拟合了,就是线性回归.直接看代码吧 import numpy as np def linear_regression(x,y): #y=bx+a,线性回归 num=len(x) b=(np.sum(x*y)-num*np.mean(x)*np.mean(y))/(np.sum(x*x)-num*np.mean(x)**2) a=np.mean(y)-b*np.mean(x)

  • python实现使用遗传算法进行图片拟合

    python实现使用遗传算法进行图片拟合

    目录 引言 预备知识及准备工作 打开图片 随机生成生物族群 按照生物性状画图 对比生物个体和目标图片的相似度 保存图片 算法主体 交叉互换 基因突变 基因片段易位 增加基因片段 减少基因片段 变异 繁殖 淘汰 拟合 示例展示 降低图片分辨率 原图 拟合过程展示 完整代码下载(已封装成类) 引言 算法思路 假设我们有这样一个生物族群,他们的每个基因片段都是一个个三角形(即只含三个点和颜色信息),他们每个个体表现出的性状就是若干个三角形叠加在一起.假设我们有一张图片可以作为这种生物族群最适应环境的性

  • Python线性回归实战分析

    Python线性回归实战分析

    一.线性回归的理论 1)线性回归的基本概念 线性回归是一种有监督的学习算法,它介绍的自变量的和因变量的之间的线性的相关关系,分为一元线性回归和多元的线性回归.一元线性回归是一个自变量和一个因变量间的回归,可以看成是多远线性回归的特例.线性回归可以用来预测和分类,从回归方程可以看出自变量和因变量的相互影响关系. 线性回归模型如下: 对于线性回归的模型假定如下: (1) 误差项的均值为0,且误差项与解释变量之间线性无关 (2) 误差项是独立同分布的,即每个误差项之间相互独立且每个误差项的方差是相等的

  • Python找出最小的K个数实例代码

    题目描述 输入n个整数,找出其中最小的K个数.例如输入4,5,1,6,2,7,3,8这8个数字,则最小的4个数字是1,2,3,4,. 这个题目完成的思路有很多,很多排序算法都可以完成既定操作,关键是复杂度性的考虑.以下几种思路当是笔者抛砖引玉,如果读者有兴趣可以自己再使用其他方法一一尝试. 思路1:利用冒泡法 临近的数字两两进行比较,按照从小到大的顺序进行交换,如果前面的值比后面的大,则交换顺序.这样一趟过去后,最小的数字被交换到了第一位:然后是次小的交换到了第二位,...,依次直到第k个数,停

随机推荐