C语言数据结构之堆、堆排序的分析及实现

目录

• 1.堆的概念结构及分类
• 1.2堆的分类
• 1.2.1 大堆
• 1.2.2 小堆
• 2. 堆的主要接口
• 3.堆的实现
• 3.1 堆的初始化 HeapInit
• 3.2 堆的销毁 HeapDestory
• 3.3 堆的打印 HeapPrint
• 3.4 堆的插入元素 HeapPush   *
• 3.5 堆的删除元素 HeapPop  *
• 4.堆的应用：堆排序   ***
• 4.1 堆排序实现过程分析
• 4.3 堆排序结果演示
• 5.堆(小堆)的完整代码
• 总结

 1.堆的概念结构及分类

以上这段概念描述看起来十分复杂，晦涩难懂。那么堆用通俗语言简单描述如下：

堆是一个完全二叉树的顺序存储。在一个堆中，堆的父节点一定大于等于(或小于等于)子节点。一旦有一部分不满足则不为堆。

堆的性质： 

1、堆中某个节点的值总是不大于或不小于其父节点的值；
2、堆总是一棵完全二叉树

1.2堆的分类

1.2.1 大堆

在一个堆中，父节点一定大于等于子节点的堆称为大堆。又称大根堆。

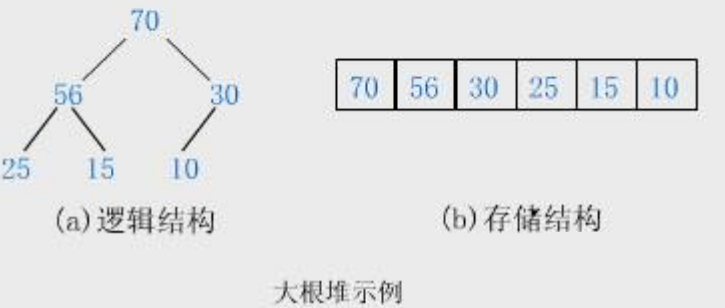
1.2.2 小堆

在一个堆中，父节点一定小于等于子节点的堆称为小堆。又称小根堆。(下图就是一个小堆)

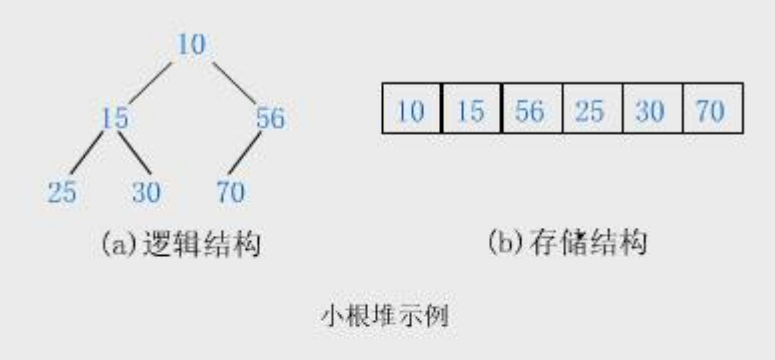
习题练习：

1.下列关键字序列为堆的是：（A）
A 100,60,70,50,32,65
B 60,70,65,50,32,100
C 65,100,70,32,50,60
D 70,65,100,32,50,60
E 32,50,100,70,65,60
F 50,100,70,65,60,32

分析：选项A分析后为大堆，其他选项多多少少都存在错误。（画图分析如下）

2. 堆的主要接口

在本篇文章中我们主要以小堆为例实现。

现实中我们通常把堆使用顺序结构的数组来存储，需要注意的是这里的堆和操作系统 虚拟进程地址空间中的堆是两回事，一个是数据结构，一个是操作系统中管理内存的一块区域分段。

其中堆中包括以下主要功能：

1.堆的初始化   2.堆销毁  3.堆打印  4.堆的插入元素  5.堆删除元素   6.判断堆是否为空  7.求堆中元素的个数  8.求堆顶元素

详细接口如下：

//小堆
//算法逻辑思想是二叉树，物理上操作的是数组中数据
typedef int HPDataType;
typedef struct Heap
{
	HPDataType* a;   //数组a
	size_t size;     //下标
	size_t capacity; //容量
}HP;

void Swap(HPDataType* pa, HPDataType* pb);//交换函数
void HeapInit(HP* php);//堆初始化
void HeapDestory(HP* php);//堆销毁
void HeapPrint(HP* php);//堆打印

//插入x以后，仍然要保证堆是（大/小）堆
void HeapPush(HP* php, HPDataType x);

//删除堆顶的数据（最大/最小）
void HeapPop(HP* php);

bool HeapEmpty(HP* php); //判断是否为空
size_t HeapSize(HP* php);//求元素个数
HPDataType HeapTop(HP* php);//求堆顶元素

3.堆的实现

有了如上的接口，接下来我们实现各个接口。由于我们使用数组来实现堆，大多接口功能和顺序表的实现相同。相同的实现这里不再过多分析。

3.1 堆的初始化 HeapInit

void HeapInit(HP* php)
{
	assert(php);
	php->a = NULL;
	php->size = php->capacity = 0;

}

3.2 堆的销毁 HeapDestory

void HeapDestory(HP* php)
{
	assert(php);
	free(php->a);
	php->a = NULL;
	php->capacity = php->size = 0;

}

3.3 堆的打印 HeapPrint

void HeapPrint(HP* php)
{
	assert(php);
	for (size_t i = 0; i < php->size; ++i)
	{
		printf("%d ", php->a[i]);
	}
	printf("\n");
}

3.4 堆的插入元素 HeapPush   *

堆的元素插入是堆的一大重点和难点。接下来我们对该功能进行分析和实现。

功能分析：

1、我们要向堆中插入元素，我们首先要判断数组是否空间已满，如果空间已满就要扩容。扩容后再将新元素插入数组尾部。此过程和顺序表相同。

2、由于插入新元素，我们要对该元素进行分析（此处以如下图小堆举例），分析插入元素是否会破坏堆结构，如果破坏了堆，我们就要对堆进行向上调整。

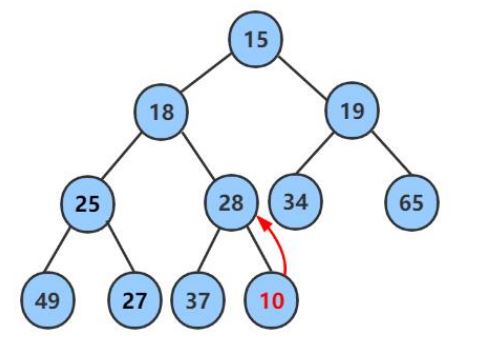
3、向上调整过程分析(过程步骤如下图)：

a. 我们发现出入新元素10之后，10作为28(父节点)的子节点却比28小，这样就破坏了我们的堆结构，这样就不构成小堆。因此我们需要对该结构进行调整。

b.由于堆的物理结构是一个数组，所以我们可以通过数组下标的形式找到我们孩子节点的父节点。不难分析出parent = (child-1)/2.当我们找到父节点时，我们进行大小比较，如果子节点小于父节点，此时就要进行交换元素。再让子节点到父节点的位置，重新计算父节点。

c.持续循环比较，如果child等于0时，说明向上调整结束。因此循环的条件可写为child>0.

注：循环过程中一旦成堆，则跳出循环。

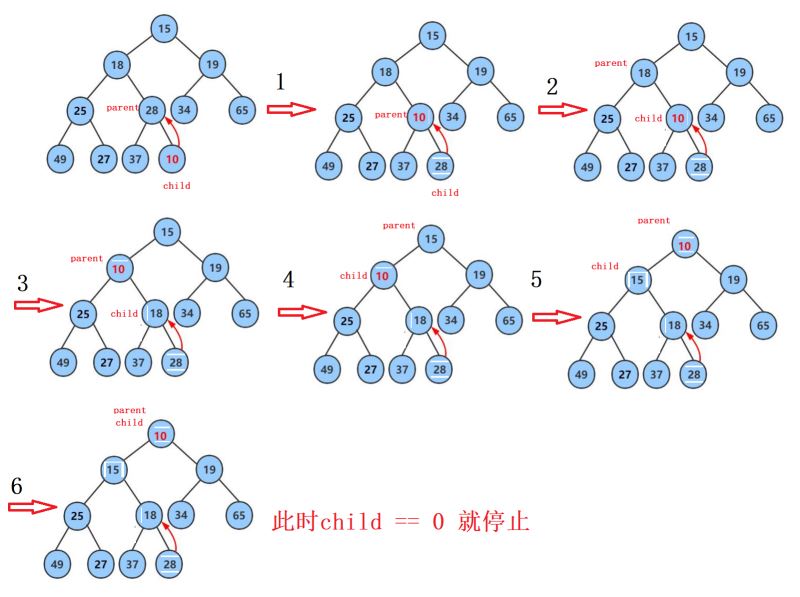
功能实现：

//交换函数
void Swap(HPDataType* pa, HPDataType* pb)
{
	HPDataType tmp = *pa;
	*pa = *pb;
	*pb = tmp;
}

//向上调整
void AdjustUp(HPDataType* a, size_t child)
{
	size_t parent = (child - 1) / 2;
	while (child > 0)
	{
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

void HeapPush(HP* php, HPDataType x)
{
	assert(php);
	//考虑是否扩容
	if (php->size == php->capacity)
	{
		size_t newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;
		HPDataType* tmp = realloc(php->a, sizeof(HPDataType) * newCapacity);
		if (tmp == NULL)
		{
			printf("realloc failed\n");
			exit(-1);
		}
		php->a = tmp;
		php->capacity = newCapacity;
	}
	php->a[php->size] = x;
	++php->size;
	//需要向上调整
	AdjustUp(php->a, php->size - 1);
}

3.5 堆的删除元素 HeapPop  *

删除堆是删除堆顶的数据 思路：将堆顶的数据跟最后一个数据一换，然后删除数组最后一个数据，再进行向下调整算法。

功能分析:

我们要删除堆是删除堆顶的数据，我们不能直接删除堆顶的数据。如果直接删除堆顶的数据，就会破坏堆结构，并且复原的复杂度较高。在这里我们介绍一种方法不仅解决了删除堆的问题，并且复杂度较低。

1、首先我们要将堆顶的数据跟最后一个数据交换，然后删除数组最后一个数据，再进行向下调整算法。

2、向下调整算法具体步骤(过程步骤如下图)：

a.我们将堆顶元素和数组最后一个元素交换后，此时堆顶的元素是数组的最后一个元素，我们要进行向下调整。定义parent为堆顶元素，查找2个子节点中较小的一个节点作为孩子节点。由于堆是数组结构实现，我们可以首先找到左孩子节点child = 2*parent+1。让左孩子和右孩子进行比较，较小的作为child的最后值。

b.如果孩子小于父亲，则交换，并继续往下调整。让parent到child的位置，再重新计算孩子。

c.当孩子大于等于元素总个数时，循环结束。因此循环的条件可以写为child<size.

注：循环过程中一旦成堆，则跳出循环。

功能实现:

void AdjustDown(HPDataType* a, size_t size, size_t root)
{
	size_t parent = root;
	size_t child = parent * 2 + 1;//先拿到左孩子
	while (child < size)
	{
		// 1、选出左右孩子中小的那个
		if (child + 1 < size && a[child + 1] < a[child])
		{
			++child;
		}

		// 2、如果孩子小于父亲，则交换，并继续往下调整
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
void HeapPop(HP* php)
{
	assert(php);
	assert(php->size > 0);
	Swap(&php->a[0], &php->a[php->size - 1]);
	--php->size;
	AdjustDown(php->a, php->size, 0);
}

3.6 判断是否为空 HeapEmpty

bool HeapEmpty(HP* php)
{
	assert(php);
	return php->size == 0;
}

3.7 求元素个数

size_t HeapSize(HP* php)
{
	assert(php);
	return php->size;
}

3.8 求堆顶元素

HPDataType HeapTop(HP* php)
{
	assert(php);
	assert(php->size > 0);
	return php->a[0];
}

4.堆的应用：堆排序   ***

堆排序即利用堆的思想来进行排序，总共分为两个步骤： 1. 建堆 升序：建大堆 降序：建小堆 2. 利用堆删除思想来进行排序 建堆和堆删除中都用到了向下调整，因此掌握了向下调整，就可以完成堆排序。

假设此时我们需要对数组元素进行升序排序，我们就可以使用我们刚刚实现的小堆。

4.1 堆排序实现过程分析

1、首先我们将数组的元素插入到堆中，根据向上调整，此时堆已经是小堆。

2、根据小堆的性质，堆顶的元素一定是该堆中最小的元素，因此我们取到堆顶的元素，再删除堆顶的元素让堆重新生成小堆。依次循环即可解决升序排序（降序排序只需将小堆改为大堆即可）。

4.2 堆排序实现代码

//堆排序
void HeapSort(int* a, int size)
{
	HP hp;
	HeapInit(&hp);
	for (int i = 0; i < size; ++i)
	{
		HeapPush(&hp, a[i]);
	}
	size_t j = 0;
	while (!HeapEmpty(&hp))
	{
		a[j] = HeapTop(&hp);
		j++;
		HeapPop(&hp);
	}
	HeapDestory(&hp);
}
int main()
{
	//	TestHeap();

	int a[] = { 4,2,1,3,5,7,9,8,6};
	HeapSort(a,sizeof(a)/sizeof(int));
	for (int i = 0; i < sizeof(a) / sizeof(int); ++i)
	{
		printf("%d ", a[i]);
	}

	return 0;
}

4.3 堆排序结果演示

5.堆(小堆)的完整代码

2022_03_30 -- 堆/2022_03_30 -- 二叉树 · 李兴宇/数据结构

总结

到此这篇关于C语言数据结构之堆、堆排序的分析及实现的文章就介绍到这了,更多相关C语言堆、堆排序实现内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！