go语言实现二叉树的序例化与反序列化

目录

• 二叉树的反序列化
• 反序列化
• 解题思路
• TreeNode结构体
• 反序列化方法
• 代码解读
• 二叉树的序列化
• 介绍
• 解题思路
• 代码
• 代码解读
• 运行结果

二叉树的反序列化

反序列化

树的反序列化故名知意就是将一个序列化成字符串或者其它形式的数据重新的生成一颗二叉树,如下这颗二叉树将它序列化成字符串后的结果[5,4,null,null,3,2,1],而现在要做的是要将这个字符串重新的生成一颗二叉树(生成下面这颗树，因为这个字符串就是通过这颗树序列化来的)。

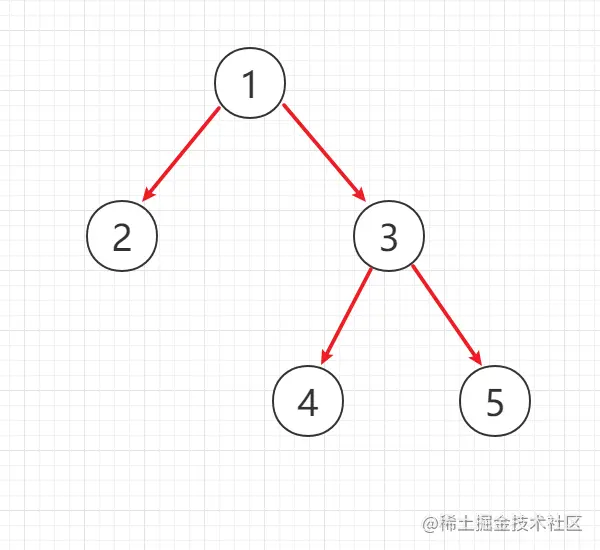
解题思路

• 首先，应该先拿到一个序列化后数据，可能是队列、栈、字符串(中间会有字符将其分割)，或其它形式的数据
• 当一个节点下面没有数据的时候，我这里采用的是用null来表示的空，比如上面节点2下面没有数据,在字符串中就用了null来表示
• 这里我将字符串转换成了队列的形式，当然使用字符串的形式也可以的，例如:通过split方法来分割成数组
• 创建一个队列，把要进行处理的节点放和主到队列里面，比如，每次循环的时候将左右分支放到这个队列里面，因为队列有FIFO的特性，在处理完左支的时候能够放便的拿到右支的node
• 接下来分析代码

TreeNode结构体

这个里面的数据很容易就看懂，val是当前节点的数据;left ,right分别保存的是左支和右支的数据

针对每个数据生成对应的TreeNode

func GenerateNode(str string) *TreeNode {
	if str == "null" {
		return nil
	}
	return &TreeNode{val: str}
}

这个方法主要是生成TreeNode对象的方法，上面说到当节点下面没有子节点的时候就会用null来表不，所以这里接收到的形参如果是null的话就会反回一个空指针，相反如果不是null就会反回一个创建的TreeNode对象，并将val属性赋值

反序列化方法

func DeserializationTb(dataQueue []string) (resultNode *TreeNode) {
	if len(dataQueue) == 0 {
		return nil
	}
	var tempNodeQueue []*TreeNode
	resultNode = generateNode(dataQueue[len(dataQueue) - 1])
	dataQueue = dataQueue[:len(dataQueue) - 1]
	if resultNode != nil {
		tempNodeQueue = append(tempNodeQueue,resultNode)
	}
	var tempNode *TreeNode
	for len(tempNodeQueue) != 0 {
		tempNode = tempNodeQueue[0]
		tempNodeQueue = tempNodeQueue[1:]
		if len(dataQueue) > 0 {
			tempNode.left = generateNode(dataQueue[len(dataQueue) - 1])
			dataQueue = dataQueue[:len(dataQueue) - 1]
			tempNode.right = generateNode(dataQueue[len(dataQueue) - 1])
			dataQueue = dataQueue[:len(dataQueue) - 1]
		}
		if tempNode.left != nil {
			tempNodeQueue = append(tempNodeQueue,tempNode.left)
		}
		if tempNode.right != nil {
			tempNodeQueue = append(tempNodeQueue,tempNode.right)
		}
	}
	return
}

代码解读

这个方法的代码比较多，这里就会块来说一下:

if len(dataQueue) == 0 {
		return nil
}

这几行代码无非就是一个边界条件的判断的问题,当传来的队列没有数据的时候就返回一个空,为啥是队列?因为我将字符串转成了队列

var tempNodeQueue []*TreeNode
resultNode = generateNode(dataQueue[len(dataQueue) - 1])
dataQueue = dataQueue[:len(dataQueue) - 1]
if resultNode != nil {
	tempNodeQueue = append(tempNodeQueue,resultNode)
}

var tempNodeQueue []*TreeNode:这里创建一个TreeNode指针数组的原因是存储要操作节点的数据,因为我将序列化后的数据转成了队列,所以在这个数组中最后一个元素应该是先出来的数组,同样第一个出来的数据是这颗二叉树的根节点,将这个节点保存到了这个队列里面,然后这个队列将在下面的for循环中使用到,其余的下面再说.

resultNode = generateNode(dataQueue[len(dataQueue) - 1]):这里便是将出队列,并通过generateNode生成一个TreeNode对象

dataQueue = dataQueue[:len(dataQueue) - 1]:因为有一个数组已经出了队列,就要将其去掉

tempNodeQueue = append(tempNodeQueue,resultNode):经过一个判空处理,便将这个节点保存到了上面提到的队列里面

for len(tempNodeQueue) != 0 {
    tempNode = tempNodeQueue[0]
    tempNodeQueue = tempNodeQueue[1:]
    if len(dataQueue) > 0 {
        tempNode.left = generateNode(dataQueue[len(dataQueue) - 1])
        dataQueue = dataQueue[:len(dataQueue) - 1]
        tempNode.right = generateNode(dataQueue[len(dataQueue) - 1])
        dataQueue = dataQueue[:len(dataQueue) - 1]
    }
    if tempNode.left != nil {
        tempNodeQueue = append(tempNodeQueue,tempNode.left)
    }
    if tempNode.right != nil {
        tempNodeQueue = append(tempNodeQueue,tempNode.right)
    }
}

当进入For循环后,也就证明现在这个队列里面有数据,不管三七二十一,先将里面的数据弹出,因为只有有了数据才可以进行下面的操作(无数据,不编程)

tempNodeQueue = tempNodeQueue[1:]:因为前一行代码将数据在这个队列里面弹出了, 所以一行代码是将已弹出的数据去除

tempNode.left = generateNode(dataQueue[len(dataQueue) - 1]):当传来序列化二叉树的存在数据的时候就将其节点的left , right分支进么赋值,下一行代码就是将弹出的数据去除,接下来的两行便是对right节点的处理,同left一样

tempNodeQueue = append(tempNodeQueue,tempNode.left):如果tempNode的左节点存在的时候就将其保存到队列中,遍历tempNodeQueue队列,再次执行上面的步骤.

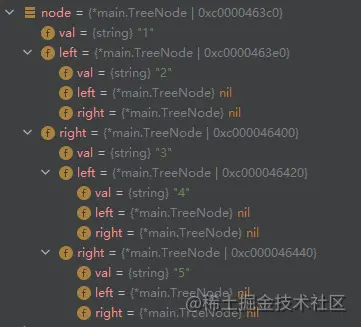
可能有小伙伴存在疑问?

所返回的resultNode变量只赋值过一次,那子节点是如何赋值的呢?因为所有的TreeNode的节点我都是通过指针来处理的,

而在For里面的第一行代码所弹出的数据指向的地址正是resultNode的地址,所以在生成完树之后,我只要抓住这颗树的根节点就好了

二叉树的序列化

介绍

树的序列化又是怎么一回事呢？我可以将这颗树转换成一定格式的数据结构，比如：转换成一段文本可以持久化到硬盘中。

那有什么作用呢？比如Redis中的数据是在内存中的，它有一个功能是每隔一段 时间可以将数据保存到硬盘中以防止突发的断电导至数据的丢失

这里说的树的序列化你也可以这样的理解，我要将一颗二叉树里面的数据序列化保存到硬盘，以便下次使用这里面的数的据的时候可以直接生成这颗树

解题思路

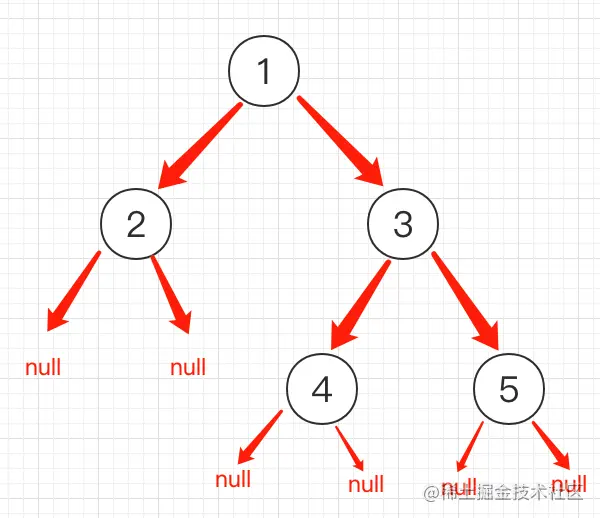
• 参于解这种题，想到的是通过对二叉树的按层来遍历来解决，当一个节点没有子节点的时候，将其视为空， 我这里用null来表示的
• 在这个里面序列化时我是先处理的左子节点，然后在处理右子节点
• 同反序列化一样，暂存数据的结构我使用的是队列的方式，还需要将获得的数据也要保存到一个队列里面
• 在程序的开始如果所给的头节点不为空，就将头节点加入到队列
• 在对队列遍历的时候弹出队列里面的数据(注:队列有FIFO的特性)，将本节点的val放到保存数据的队列里面
• 依次将本节点的左子节点和右子节点放到队列里面，在次执行上述步骤

代码

/**
序列化二叉树
*/
func SerializationTb(bt *TreeNode) (saveSerData []string) {
	root := bt
	var tempQueue []*TreeNode
	if root != nil {
		tempQueue = append(tempQueue, root)
	}
	var tempNode *TreeNode
	for len(tempQueue) != 0 {
		tempNode = tempQueue[0]
		if tempNode != nil {
			saveSerData = append(saveSerData, tempNode.val)
		} else {
			saveSerData = append(saveSerData, "null")
		}
		tempQueue = tempQueue[1:]
		if tempNode != nil {
			tempQueue = append(tempQueue, tempNode.left)
			tempQueue = append(tempQueue, tempNode.right)
		}
	}
	return
}

代码解读

这些代码还是很好看懂的，这里就说下for里面的代码吧~~

tempNode = tempQueue[0]:在队列里面弹出一个数据

saveSerData = append(saveSerData, tempNode.val):将tempNode的val属性保存到saveSerData队列里面

下面的if就是判断当这个节点为空或者是不为空的时候需要分别怎么处理数据，上面说到如果一个节点下面没有子节点，这里就用null来表示，所以当没有子节点的时候就用将null添加到队列里面

tempQueue = tempQueue[1:]:对队列重新赋值，将弹出的那个数据去掉

tempQueue = append(tempQueue, tempNode.left):将左节点加入到队列里面，下一行同理

运行结果

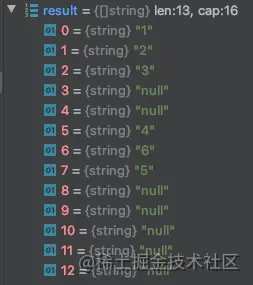
到此这篇关于go语言实现二叉树的序例化与反序列化的文章就介绍到这了,更多相关go序例化内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！