Golang 处理浮点数遇到的精度问题(使用decimal)
目录
- 一、浮点数是什么?
- 1.指数方案
- 2.规范化指数形式
- 3.IEEE754标准
- 二、出现精度问题的情况
- 1.浮点数加减运算
- 2.float64与float32之间转换
- 3.int64和float64,int32和float32转换
- 4.float64位直接乘100
- 三、decimal解决精度问题
- 1.浮点数加减运算
- 2.float64与float32之间转换
- 3.float64位直接乘100
- 总结
一、浮点数是什么?
浮点数,是属于有理数中某特定子集的数的数字表示,在计算机中用以近似表示任意某个实数。浮点数在计算机中主要用来表示小数,浮点数就是小数点可以出现改变的数字。
因为在计算机的机器语言中,只有二进制,机器语言只能识别0和1。所以,计算机也是不可能存储小数的,所以需要有另一种变通的存储方案。
这种方案就是:
1.指数方案
指数形式:其数值部分是一个小数,小数点前的数字是零,小数点后的第一位数字不是零。一个实数可以有多种指数表示形式,但只有一种属于标准化指数形式。
| 12.3 | 1.23*10^-1 |
| 1.23 | 1.23*10^0 |
| 1.23 | 0.123*10^1 |
上面的表格,我们可以很清晰的了解指数方案。同样的我们也就能发现这样表达小数会有一个严重的问题,那就是指数表示形式太多了,如果不能约定好唯一形式,不同代码之间沟通将会出现问题。
2.规范化指数形式
在指数形式的多种表示方式中把小数部分中小数点前的数字为0、小数点后第1位数字不为0的表示形式称为规范化的指数形式。
1.23 的规范化的指数形式 0.123*10^1
一个实数只有一个规范化的指数形式,在程序以指数形式输出一个实数时,必然以规范化的指数形式输出。
0.123e001
1.为什么要以 0 开头
1.23456要二进制存放需分别存整数部和小数部,而0.123456则只需存小数部,这样在占用相同字节的情况下,后一种方法可容纳更大精度的浮点数。
2.为什么 e 后面要加 0 ,e001 和 e1 一样吗
后面加 0 是 %e 的输出格式,并不是规范化的指数形式所必需的,
e001 和 e1 是一样的
3.IEEE 754标准
由于不同机器对浮点数的表示有较大差别,这不利于软件在不同计算机之间的移植。为此,美国IEEE提出了一个从系统角度支持浮点数的表示方法,称为IEEE754标准(IEEE,1985),当今流行的计算机几乎都采用了这一标准。
IEEE 754规定了四种表示浮点数值的方式:单精确度(32位)、双精确度(64位)、延伸单精确度(43比特以上,很少使用)与延伸双精确度(79比特以上,通常以80位实现)。只有32位模式有强制要求,其他都是选择性的。
二、出现精度问题的情况
1.浮点数加减运算
输入数据:
a = 2.3329 b = 3.1234
代码如下(示例):
package main
import "fmt"
func main() {
// a = 2.3329 b = 3.1234
a, b := 2.3329, 3.1234
c := a + b
fmt.Println(c) //5.456300000000001}
}
结果精度出现问题
2.3329 + 3.1234 = 5.456300000000001
已经出错
2.float64与float32之间转换
输入数据:
a = 9.99999
代码如下(示例):
package main
import "fmt"
func main() {
var a float32
a = 9.99999
b := float64(a)
fmt.Println(b) //9.999990463256836}
}
结果精度出现问题
9.99999 = 9.999990463256836
已经出错
3.int64和float64,int32和float32转换
1.int32和float32转换
输入数据:
a = 9.99999
代码如下(示例):
package main
import "fmt"
func main() {
var a int32
a = 999990455
b := float32(a)
fmt.Printf("%f\n", b) //999990464.000000}
}
结果精度出现问题
999990455= 999990464.000000
已经出错
2.int64和float64转换
输入数据:
a = 999999942424527242
代码如下(示例):
package main
import "fmt"
func main() {
var a int64
a = 999999942424527242
b := float64(a)
fmt.Printf("%f\n", b) //999999942424527232.000000}
}
结果精度出现问题
999999942424527242 = 999999942424527232.000000
已经出错
4.float64位直接乘100
输入数据:
a = 999999942424527242
代码如下(示例):
package main
import "fmt"
func main() {
var a float64
a = 1128.61
b := a * 100
fmt.Println(b) //112860.99999999999}
}
结果精度出现问题
1128.61 * 100= 112860.99999999999
已经出错
三、decimal 解决精度问题
利用 Decimal 包解决精度问题
go get github.com/shopspring/decimal
1.浮点数加减运算
输入数据:
a = 2.3329 b = 3.1234
代码如下(示例):
package main
import (
"fmt"
"github.com/shopspring/decimal"
)
func main() {
// a = 2.3329 b = 3.1234
a, b := 2.3329, 3.1234
c := decimal.NewFromFloat(a)
d := decimal.NewFromFloat(b)
fmt.Println(a, b)
fmt.Println(c, d)
fmt.Println("此时ab 与 cd 相同")
fmt.Println(a + b) //5.456300000000001}
fmt.Println(c.Add(d)) //5.4563}
}
结果精度不再出现问题

2.float64与float32之间转换
输入数据:
a = 9.99999
代码如下(示例):
package main
import (
"fmt"
"github.com/shopspring/decimal"
)
func main() {
var a float32
a = 9.99999
c := decimal.NewFromFloat32(a)
b := float64(a)
c.Float64()
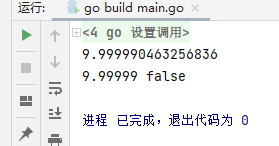
fmt.Println(b) //9.999990463256836}
fmt.Println(c.Float64()) //9.99999}
}
结果精度不再出现问题
3.float64位直接乘100
输入数据:
a = 999999942424527242
代码如下(示例):
package main
import (
"fmt"
"github.com/shopspring/decimal"
)
func main() {
var a float64
a = 1128.61
c := decimal.NewFromFloat(a)
b := a * 100
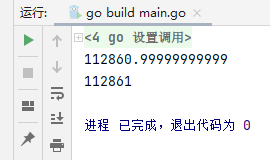
fmt.Println(b) //112860.99999999999}
fmt.Println(c.Mul(decimal.NewFromInt(100))) //112861}
}
结果精度不再出现问题
总结
通过以上两个例子,我们已经了解了浮点数的精度问题,那么在工作中,我们就需要更换运算方式。我们需要尽量选择Decimal,否则如果使用 Float 出现精度问题之后,到那时再更换方法,既费时又费力,能刚开始就解决,何乐而不为呢。
到此这篇关于Golang 处理浮点数遇到的精度问题(使用decimal)的文章就介绍到这了,更多相关Golang 浮点精度内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们!

