C++实现矩阵对称正交化的示例代码

1.python代码

import numpy as np
import pandas as pd
df=pd.DataFrame()
df['fac_01']=(34, 45, 65)
df['fac_02']=(56, 25, 94)
print(df)
print('------------------矩阵的特征跟D、和特征向量U-----------------------')
D,U=np.linalg.eig(np.dot(df.T, df)) # 求矩阵的特征跟D、和特征向量U
print(D,U,sep='\n')
print('\n------------------对角矩阵-----------------------')
print(np.diag(D**(-0.5)))
print('\n------------------对称正交后的矩阵-----------------------')
S = np.dot(np.dot(U, np.diag(D**(-0.5))), U.T) # 求过渡矩阵S = U* DEx *U'
F_hat = np.dot(df, S) # 求对称正交后的矩阵
print(F_hat)

2.C++的Eigen库实现

#include "Eigen/Dense"
using namespace Eigen;
int main()
{
    //初始化
    MatrixXf A(3, 2);
    A(0,0) = 34;A(0,1) = 56;
    A(1,0) = 45;A(1,1) = 25;
    A(2,0) = 65;A(2,1) = 94;
    //生成正交矩阵
    MatrixXf AEx = A.transpose() * A;
    int nRowSize = AEx.rows();
    int nColSize = AEx.cols();
    //求特征根、特征向量
    SelfAdjointEigenSolver<Matrix2f> eigensolver(AEx);
    MatrixXf D = eigensolver.eigenvalues();
    MatrixXf U = eigensolver.eigenvectors();
    std::cout<<"特征根如下：" <<std::endl;
    nRowSize = D.rows();
    nColSize = D.cols();
    for(size_t i=0; i<nRowSize; i++)
    {
        for(size_t j=0; j<nColSize; j++)
        {
            std::cout<<D(i,j)<<"    ";
        }
        std::cout<<std::endl;
    }
    std::cout<<"特征向量如下：" <<std::endl;
    nRowSize = U.rows();
    nColSize = U.cols();
    for(size_t i=0; i<nRowSize; i++)
    {
        for(size_t j=0; j<nColSize; j++)
        {
            std::cout<<U(i,j)<<"    ";
        }
        std::cout<<std::endl;
    }
    //生成np.diag(D**(-0.5)))对角线矩阵
    MatrixXf DEx(2,2);
    for(size_t i=0; i<2; i++)
    {
        for(size_t j=0; j<2; j++)
        {
            if(i == j)
            {
                DEx(i,j) = pow(D(i,0),-0.5);
            }
            else
            {
                DEx(i,j) = 0;
            }
        }
    }
    nRowSize = DEx.rows();
    nColSize = DEx.cols();
    std::cout<<"对角线矩阵如下：" <<std::endl;
    for(size_t i=0; i<nRowSize; i++)
    {
        for(size_t j=0; j<nColSize; j++)
        {
            std::cout<<DEx(i,j)<<"    ";
        }
        std::cout<<std::endl;
    }
    //生成过度矩阵S
    MatrixXf S = U * DEx * U.transpose();
    //生成正交化矩阵
    MatrixXf R = A * S;
    nRowSize = R.rows();
    nColSize = R.cols();
    std::cout<<"正交化结果如下：" <<std::endl;
    for(size_t i=0; i<nRowSize; i++)
    {
        for(size_t j=0; j<nColSize; j++)
        {
            std::cout<<R(i,j)<<"    ";
        }
        std::cout<<std::endl;
    }
	return 0;
}

3.结果对比

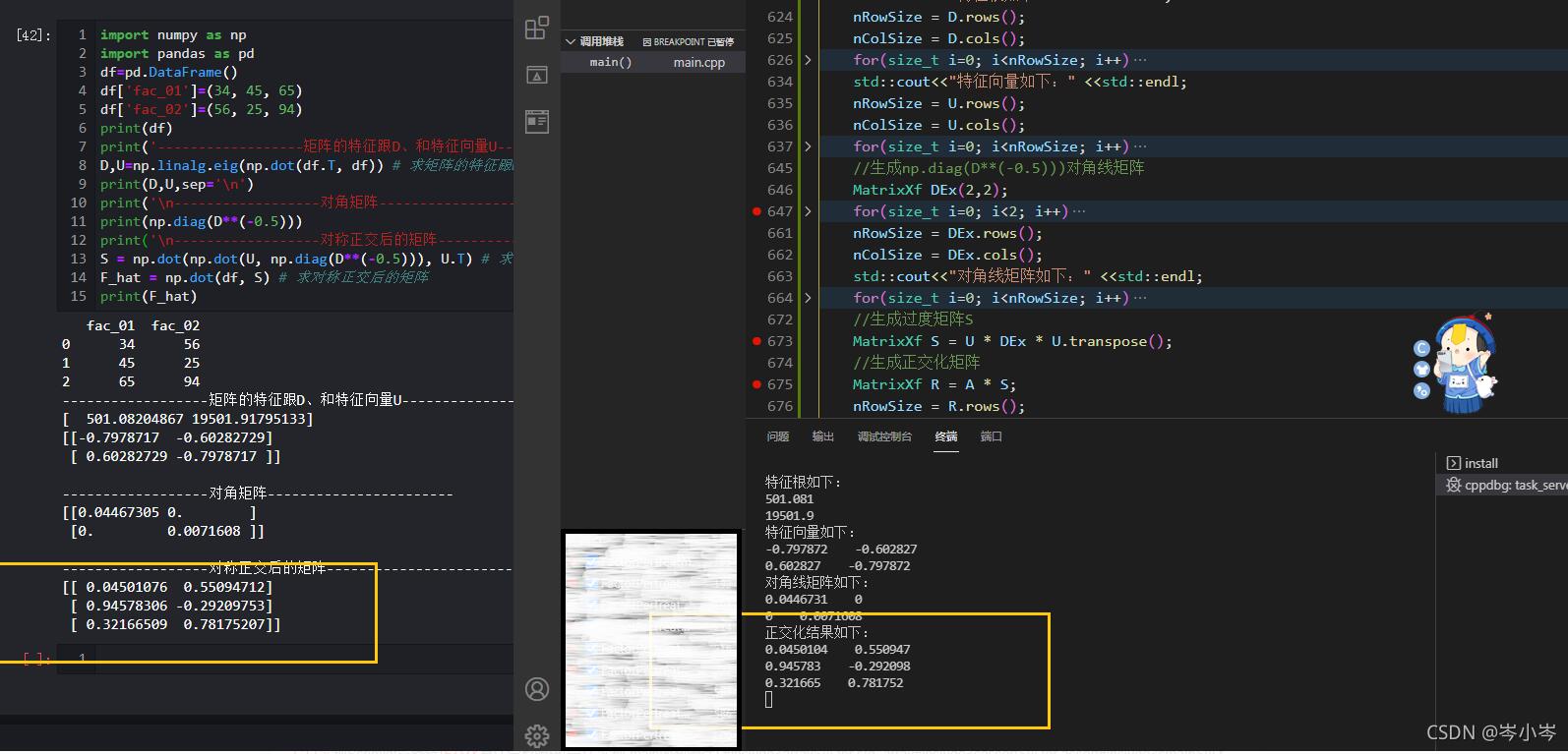
到此这篇关于C++实现矩阵对称正交化的文章就介绍到这了,更多相关C++矩阵对称正交化内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！