R语言数据预处理操作——离散化(分箱)
一、项目环境
开发工具:RStudio
R:3.5.2
相关包:infotheo,discretization,smbinning,dplyr,sqldf
二、导入数据
# 这里我们使用的是鸢尾花数据集(iris) data(iris) head(iris)
| Sepal.Length | Sepal.Width | Petal.Length | Petal.Width | Species | |
|---|---|---|---|---|---|
| 1 | 5.1 | 3.5 | 1.4 | 0.2 | setosa |
| 2 | 4.9 | 3.0 | 1.4 | 0.2 | setosa |
| 3 | 4.7 | 3.2 | 1.3 | 0.2 | setosa |
| 4 | 4.6 | 3.1 | 1.5 | 0.2 | setosa |
| 5 | 5.0 | 3.6 | 1.4 | 0.2 | setosa |
| 6 | 5.4 | 3.9 | 1.7 | 0.4 | setosa |
相关数据解释:
Sepal.Length:萼片长度
Sepal.Width:萼片宽度
Petal.Length:花瓣长度
Petal.Width:花瓣宽度
Species:鸢尾花品种
三、 数据划分
library(dplyr)
library(sqldf)
# 为数据集增加序号列(id)
iris$id <- c(1:nrow(iris))
# 将鸢尾花数据集中70%的数据划分为训练集
iris_train <- sample_frac(iris, 0.7, replace = TRUE)
# 使用sql语句将剩下的30%花费为测试集
iris_test <- sqldf("
select *
from iris
where id not in (
select id
from iris_train
)
")
# 去除序号列(id)
iris_train <- iris_train[,-6]
iris_test <- iris_test[,-6]
【注】:这里使用到sqldf包的函数sqldf函数来时间在R语言中使用SQL语句
四、 无监督分箱
常见的几种无监督分箱方法
等宽分箱法
等频分箱法
kmeans分箱法
1、 分箱前准备法
# 导入无监督分箱包——infotheo library(infotheo) # 分成几个区域 nbins <- 3
2、 等宽分箱法
### 等宽分箱的原理非常简单,就是按照相同的间距将数据分成相应的等分 # 将连续型数据分成三份,并以1、2、3赋值 equal_width <- discretize(iris_train$Sepal.Width,"equalwidth",nbins) ### 查看分箱情况 # 查看各分类数量 table(equal_width) # 用颜色表明是等宽分箱 plot(iris_train$Sepal.Width, col = equal_width$X) ### 保存每个等分切割点的值(阙值) # 计算各个分类相应的切割点 width <- (max(iris_train$Sepal.Width)-min(iris_train$Sepal.Width))/nbins # 保存阙值 depreciation <- width * c(1:nbins) + min(iris_train$Sepal.Width)

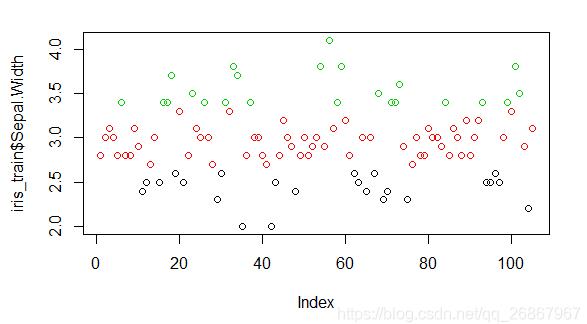
3、 等频分箱
### 等频分箱是将数据均匀的分成相应的等分(数量不一定是完全相同的) # 将连续型数据分成三份,并以1、2、3赋值 equal_freq <- discretize(iris_train$Sepal.Width,"equalfreq",nbins) ### 查看分箱情况 # 查看各分类数量 table(equal_width) # 用颜色表明是等频分箱 plot(iris_train$Sepal.Width, col = equal_freq$X) ### 保存每个等分切割点的值(阙值) data <- iris_train$Sepal.Width[order(iris_train$Sepal.Width)] depreciation <- as.data.frame(table(equal_freq))$Freq

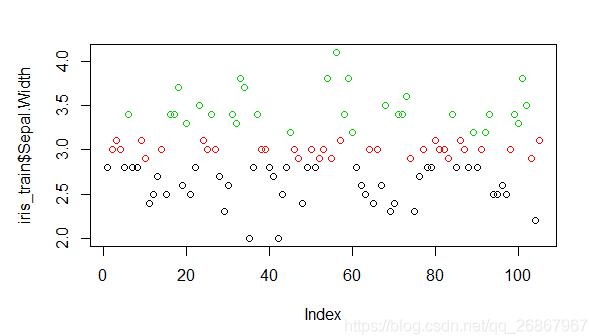
4、kmeans分箱法
# kmeans分箱法,先给定中心数,将观察点利用欧式距离计算与中心点的距离进行归类,再重新计算中心点,直到中心点# 不再发生变化,以归类的结果做为分箱的结果。 # 将连续型数据分成三份,并以1、2、3赋值 k_means <- kmeans(iris_train$Sepal.Width, nbins) # 查看各分类数量 table(k_means$cluster) # 查看实际分箱状况 k_means$cluster # 保存阙值 # rev() 的作用是倒置数据框 # 统一从左往右,从大到小 depreciation <- rev(k_means$centers)

五、 有监督分箱
discretization提供了几个主要的离散化的工具函数:
chiM,ChiM算法进行离散化
chi2, Chi2算法进行离散化
mdlp,最小描述长度原理(MDLP)进行离散化
modChi2,改进的Chi2方法离散数值属性
disc.Topdown,自上而下的离散化
extendChi2,扩展Chi2算法离散数值属性
smbinning提供的工具函数:
smbinning ,基于构造条件推断树ctree的监督式分箱
1、chiM算法进行离散化
### 有监督的数据离散化 library(discretization)# 有监督分箱 # 使用ChiMerge算法基于卡方检验进行自下而上的合并 chi1 <- chiM(iris_train, alpha = 0.05) # alpha 为显著性指标 apply(chi1$Disc.data,2,table) # 保存阙值 depreciation <- chi1$cutp[[2]] ## 其他有监督分享算法 # chi2 <- chi2(iris,alp=0.5,del=0.05) # chi2()算法 # chi3 <- modChi2(iris,alp=0.5) # modChi2()算法 # chi4 <- extendChi2(iris,alp = 0.5) # extendChi2()算法 # m1 <- mdlp(iris) # 使用熵准则将最小描述长度作为停止规则来离散化 # d1 <- disc.Topdown(iris,method=1) # 该功能实现了三种自上而下的离散化算法(CAIM,CACC,Ameva)

2、基于构造条件推断树ctree的监督式分箱
# 分箱前数据准备 library(smbinning) # 查看测试用例 head(smbsimdf1)
| fgood | cbs1 | cbs2 | cbinq | cbline | cbterm | cblineut | cbtob | cbdpd | cbnew | pmt | tob | dpd | dep | dc | od | home | inc | dd | online | rnd | period |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 60.11 | NA | 02 | 2 | 00 | 47.51361 | 5 | No | No | M | 2 | 00No | 10481.40 | 20 | 01 | No | W06 | 00 | Yes | 0.46641029 | 2018-03-31 |
| 1 | 45.62 | 66.72 | 02 | 2 | 02 | 52.36222 | 4 | No | No | A | 1 | 02Hi | 10182.43 | 17 | 01 | No | W10 | 00 | Yes | 0.91980286 | 2018-05-31 |
| 1 | 30.86 | 66.94 | 02 | 2 | 00 | 35.89640 | 5 | No | Yes | M | 2 | 02Hi | 9645.37 | 23 | 00 | No | W05 | 00 | Yes | 0.33804009 | 2018-07-31 |
| 1 | 62.38 | 49.12 | 02 | 3 | 01 | 41.93578 | 6 | No | No | P | 4 | 00No | 13702.76 | 31 | 01 | No | 00 | Yes | 0.76475600 | 2017-12-31 | |
| 1 | 54.36 | 41.22 | 00 | 1 | 00 | 44.23662 | 5 | No | No | P | 4 | 00No | 18720.09 | 26 | 02 | Yes | W08 | 01 | Yes | 0.58563795 | 2018-02-28 |
| 1 | 68.78 | 50.80 | 00 | 0 | 00 | 43.59248 | 7 | Yes | Yes | A | 4 | 01Lo | 10217.07 | 31 | 00 | No | W09 | 00 | Yes | 0.05756396 | 2018-03-31 |
【注】:这里之所以不适用鸢尾花数据集的原因在于,这个函数的使用条件较为苛刻。首先它不允许数据集的列名中含有 “.” ,比如 鸢尾花数据集中的“Sepal.Width”就不可以。
其次它要求用于学习的列必须是二分类,且数据类型必须是numeric,二分类的值也必须是(0, 1) 。也是因为这些原因,为了方便在这里使用包中自带的数据集。
# 使用smbinning函数进行分箱,df 为原始数据,y表示目标标签,x表示需要分箱的标签result <- smbinning(df = smbsimdf1,y = "fgood",x = "cbs1") # 查看分箱结果的分布情况,不良率和证据权重 par(mfrow=c(2,2)) boxplot(smbsimdf1$cbs1~smbsimdf1$fgood,horizontal=T, frame=F, col="lightgray",main="Distribution") smbinning.plot(result,option="dist") smbinning.plot(result,option="badrate") smbinning.plot(result,option="WoE")
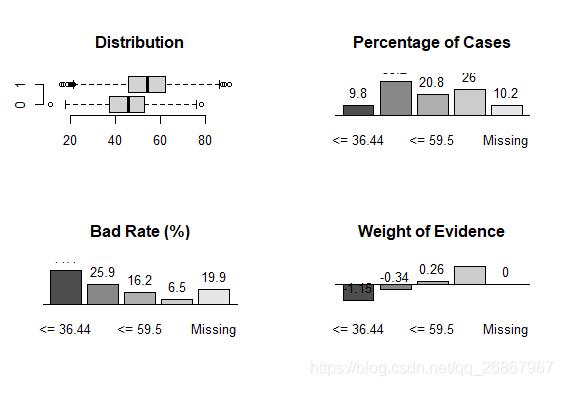
result$ivtable # 相关重要信息 result$ctree # 决策树 result$cuts # 阙值 smbinning.sql(result) # 输出相应的sql语句

# 使用训练好的函数对数据进行分箱(训练集和测试集都需要) smbsimdf1 <- smbinning.gen(smbsimdf1, result, chrname = "gcbs1") # 查看分箱情况 table(smbsimdf1$gcbs1)
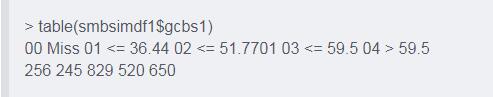
【注】:除此之外也可以用smbinning.sql(result) 生成的sql语句,配合sqldf包进行数据分箱操作。
六、 使用阙值对测试集进行分箱操作
上述方法中,除了最后一种方法,我们都没有将训练好的函数用于测试集。但是在实际的分析,我们让数据离散化最主要的目的更多的是为了降低机器学习的负担。
因此我们除了需要对训练集进行分箱操作之外,将同样的分箱方法作用与测试集。那么下面我们就将使用之前得到的阙值,对测试集进行分享操作。
### 对测试集进行分箱操作
# 使用之前保存的阙值
# 这里之所以要前后加上Inf,是为了让它的范围能够向正负无穷延伸
# (-Inf, a],[b, Inf)
break1<-c(-Inf,depreciation,Inf)
labels = c("差", "中", "良", "优")
# 第一个值是数据
# 第一个值是分箱的区间
# 第三个值是替换成的数
# ordered_result表示被替换成的数是否有前后顺序
iris_test$Sepal.Width <- cut(iris_test$Sepal.Width,break1,labels,ordered_result = T)
iris_test$Sepal.Width
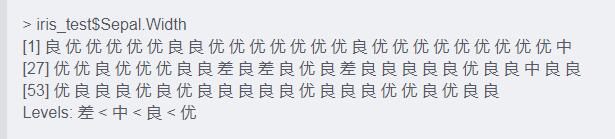
七、 结语
本文更多的是从实际操作的角度进行说明,之间涉及到的很多算法的原理没有进行过多的说明。
以上为个人经验,希望能给大家一个参考,也希望大家多多支持我们。如有错误或未考虑完全的地方,望不吝赐教。

