C++实现蓝桥杯竞赛题目---搭积木

小明对搭积木非常感兴趣。他的积木都是同样大小的正立方体。
在搭积木时，小明选取 m 块积木作为地基，将他们在桌子上一字排开，中间不留空隙，并称其为第0层。
随后，小明可以在上面摆放第1层，第2层，……，最多摆放至第n层。摆放积木必须遵循三条规则

规则1：每块积木必须紧挨着放置在某一块积木的正上方，与其下一层的积木对齐；

规则2：同一层中的积木必须连续摆放，中间不能留有空隙；

规则3：小明不喜欢的位置不能放置积木。

其中，小明不喜欢的位置都被标在了图纸上。图纸共有n行，从下至上的每一行分别对应积木的第1层至第n层。每一行都有m个字符，字符可能是‘.'或‘X'，其中‘X'表示这个位置是小明不喜欢的。
现在，小明想要知道，共有多少种放置积木的方案。他找到了参加蓝桥杯的你来帮他计算这个答案。
由于这个答案可能很大，你只需要回答这个答案对1000000007(十亿零七)取模后的结果。
注意：地基上什么都不放，也算作是方案之一种。

输入格式：
数据的第一行有两个正整数n和m，表示图纸的大小。
随后n行，每行有m个字符，用来描述图纸 。每个字符只可能是‘.'或‘X'。

输出格式：
一个整数，表示答案对1000000007取模后的结果。

输入样例1：

2 3

..X

.X.

输出样例1：

4

输入样例2：

3 3

..X

.X.

...

输出样例2：

16

解题思路：

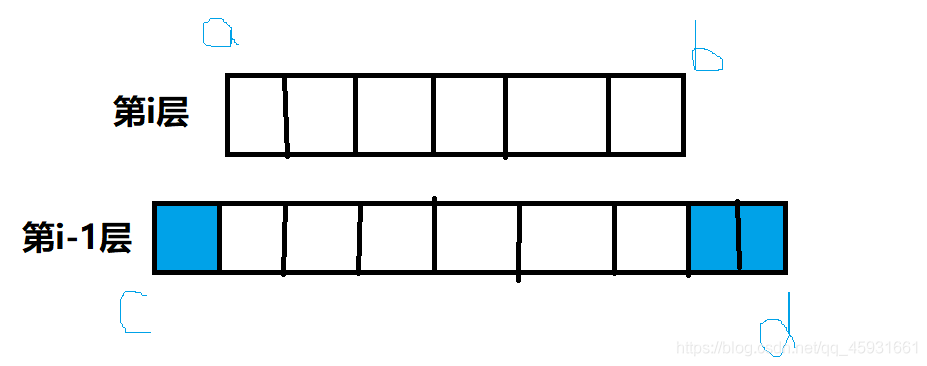
首先先推导出递推式，观察题目，可以得到递推式为：

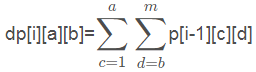
用代码表示即为：

for(int c=1;c<a;c++){
	for(int d=b;d<m;d++){
		dp[i][a][b]+=dp[i-1][c][d];
	}
}

意思是
在第i层的a到b长度放置积木的可能数=在i-1层的所有包含a到b的长度的积木的可能数的和。

除了单纯的判断递推式以外，还需要考虑一种特殊情况，就是积木放置的长度中存在X，即小明不想放的位置，那么就不需要进行递推，直接返回0。
判断[a,b]是否存在X，可以用前缀和来判断，节省时间。
前缀和初始化为：

s[i][j] = s[i][j-1] + (temp=='X');

推导出递推式以后可以很容易的写出代码：

#include<iostream>

using namespace std;

const int N = 30;
int n, m;
int dp[30][30][30];
int s[30][30];
int cnt=1;

int main() {
	cin >> n >> m;
	getchar();
	for (int i = n; i >0; i--) {//初始化前缀和
		for (int j = 1; j <= m; j++) {
			char temp = getchar();
			s[i][j] = s[i][j-1] + (temp=='X');
		}
		getchar();
	}
	dp[0][1][m]=1;//第0层，长度从1到m的积木有一种可能
	for (int i = 1; i <=n; i++) {//第i层
		for (int a = 1; a <= m; a++) {
			for (int b = a; b <= m; b++) {
				if (s[i][b] - s[i][a - 1] != 0) {//a到b区间存在X
					dp[i][a][b] = 0;
					continue;
				}
				for (int c = 1; c <= a; c++) {
					for (int d = b; d <= m; d++) {
						dp[i][a][b] += dp[i - 1][c][d];
					}
				}
				cnt += dp[i][a][b];//记录数量
			}
		}
	}
	cout << cnt;
	return 0;
}

优化

但是仔细一想，五个for循环无法通过最后50%的测试点，所以需要进行优化，观察最内层的两个c，d的for循环可知，有如下图像：

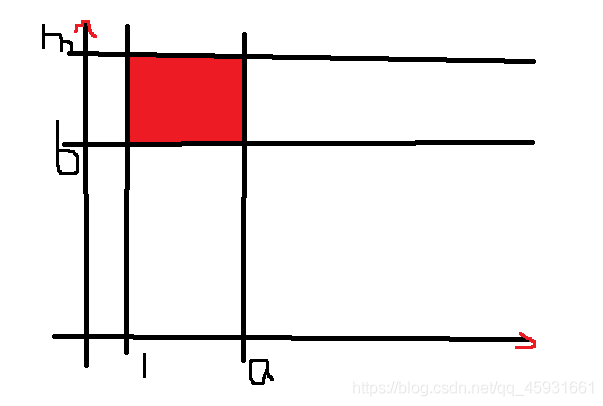
实际上最内层的两个循环就是在求第i-1层的红色区域面积。
那我们再利用二维的前缀和进行存储，那就可以优化掉两个循环，从而使时间复杂度降低，通过最后的测试点。

#include<iostream>

using namespace std;

const int N = 30;
const int mod = 1e9 + 7;
int n, m;
int dp[30][30][30];
int s[30][30];//用来判断是否存在X
int sum[30][30];//指的是左下角所有dp[i][][]的和
int cnt=1;

void get_fixsum(int i) {
	//更新第i层的前缀和数组
	for (int a = 1; a <= m; a++) {
		for (int b = 1; b <= m; b++) {
			sum[a][b] =(sum[a][b-1]+sum[a-1][b]-sum[a-1][b-1]+ dp[i][a][b])%mod;
		}
	}
}

int main() {
	cin >> n >> m;
	getchar();
	for (int i = n; i >0; i--) {
		for (int j = 1; j <= m; j++) {
			char temp = getchar();
			s[i][j] = s[i][j-1] + (temp=='X');
		}
		getchar();
	}
	dp[0][1][m]=1;//第0层，长度从1到m的积木有一种可能
	get_fixsum(0);
	for (int i = 1; i <=n; i++) {//层数
		for (int a = 1; a <= m; a++) {
			for (int b = a; b <= m; b++) {
				if (s[i][b] - s[i][a - 1] != 0) {//a到b区间存在X
					dp[i][a][b] = 0;
					continue;
				}
				dp[i][a][b] = (sum[a][m] - sum[0][m] - sum[a][b-1] + sum[0][b-1])%mod;
				cnt =(cnt+ dp[i][a][b])%mod;
			}
		}
		get_fixsum(i);
	}
	cout << (cnt+mod)%mod;//防止出现负数
	return 0;
}

到此这篇关于C++实现蓝桥杯竞赛题目---搭积木的文章就介绍到这了,更多相关C++实现蓝桥杯---搭积木内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！