深入解析神经网络从原理到实现

1.简单介绍

在机器学习和认知科学领域，人工神经网络（artificial neural network，缩写ANN），简称神经网络（neural network，缩写NN）或类神经网络，是一种模仿生物神经网络(动物的中枢神经系统，特别是大脑)的结构和功能的数学模型或计算模型，用于对函数进行估计或近似。神经网络由大量的人工神经元联结进行计算。大多数情况下人工神经网络能在外界信息的基础上改变内部结构，是一种自适应系统。现代神经网络是一种非线性统计性数据建模工具。典型的神经网络具有以下三个部分：

结构 （Architecture） 结构指定了网络中的变量和它们的拓扑关系。例如，神经网络中的变量可以是神经元连接的权重（weights）和神经元的激励值（activities of the neurons）。

激励函数（Activity Rule） 大部分神经网络模型具有一个短时间尺度的动力学规则，来定义神经元如何根据其他神经元的活动来改变自己的激励值。一般激励函数依赖于网络中的权重（即该网络的参数）。

学习规则（Learning Rule）学习规则指定了网络中的权重如何随着时间推进而调整。这一般被看做是一种长时间尺度的动力学规则。一般情况下，学习规则依赖于神经元的激励值。它也可能依赖于监督者提供的目标值和当前权重的值。

2.初识神经网络

如上文所说，神经网络主要包括三个部分：结构、激励函数、学习规则。图1是一个三层的神经网络，输入层有d个节点，隐层有q个节点，输出层有l个节点。除了输入层，每一层的节点都包含一个非线性变换。

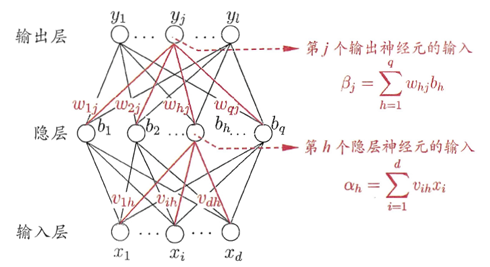
图1

那么为什么要进行非线性变换呢？

（1）如果只进行线性变换，那么即使是多层的神经网络，依然只有一层的效果。类似于0.6*(0.2x1+0.3x2)=0.12x1+0.18x2。
（2）进行非线性变化，可以使得神经网络可以拟合任意一个函数,图2是一个四层网络的图。

图2

下面使用数学公式描述每一个神经元工作的方式

（1）输出x
（2）计算z=w*x
（3）输出new_x = f(z)，这里的f是一个函数，可以是sigmoid、tanh、relu等，f就是上文所说到的激励函数。

3.反向传播(bp)算法

有了上面的网络结构和激励函数之后，这个网络是如何学习参数（学习规则）的呢？

首先我们先定义下本文使用的激活函数、目标函数

（1）激活函数（sigmoid）：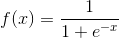

def sigmoid(z):
  return 1.0/(1.0+np.exp(-z))

sigmoid函数有一个十分重要的性质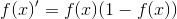：，即计算导数十分方便。

def sigmoid_prime(z):
  return sigmoid(z)*(1-sigmoid(z))

下面给出一个简单的证明：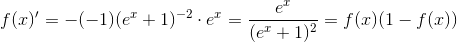

（2）目标函数（差的平方和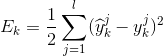），公式中的1/2是为了计算导数方便。

然后，这个网络是如何运作的

（1）数据从输入层到输出层，经过各种非线性变换的过程即前向传播。

def feedforward(self, a):
  for b, w in zip(self.biases, self.weights):
    a = sigmoid(np.dot(w, a)+b)
  return a

其中，初始的权重（w）和偏置（b）是随机赋值的

biases = [np.random.randn(y, 1) for y in sizes[1:]]
weights = [np.random.randn(y, x) for x, y in zip(sizes[:-1], sizes[1:])]

（2）参数更新，即反向传播

在写代码之前，先进行推导，即利用梯度下降更新参数，以上面的网络结构（图1）为例

（1）输出层与隐层之间的参数更新

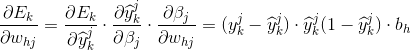
（2）隐层与输入层之间的参数更新

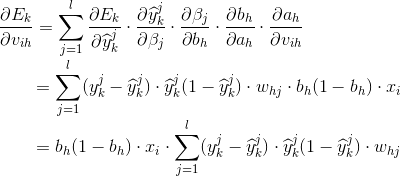
有两点需要强调下：

（2）中的结果比（1）中的结果多了一个求和公式，这是因为计算隐层与输入层之间的参数时，输出层与隐层的每一个节点都有影响。

（2）中参数更新的结果可以复用（1）中的参数更新结果，从某种程度上，与反向传播这个算法名称不谋而合，不得不惊叹。

def backprop(self, x, y):
  """返回一个元组(nabla_b, nabla_w)代表目标函数的梯度."""
  nabla_b = [np.zeros(b.shape) for b in self.biases]
  nabla_w = [np.zeros(w.shape) for w in self.weights]
  # feedforward
  activation = x
  activations = [x] # list to store all the activations, layer by layer
  zs = [] # list to store all the z vectors, layer by layer
  for b, w in zip(self.biases, self.weights):
    z = np.dot(w, activation)+b
    zs.append(z)
    activation = sigmoid(z)
    activations.append(activation)
  # backward pass
  delta = self.cost_derivative(activations[-1], y) * \
    sigmoid_prime(zs[-1])
  nabla_b[-1] = delta
  nabla_w[-1] = np.dot(delta, activations[-2].transpose())
  """l = 1 表示最后一层神经元，l = 2 是倒数第二层神经元, 依此类推."""
  for l in xrange(2, self.num_layers):
    z = zs[-l]
    sp = sigmoid_prime(z)
    delta = np.dot(self.weights[-l+1].transpose(), delta) * sp
    nabla_b[-l] = delta
    nabla_w[-l] = np.dot(delta, activations[-l-1].transpose())
  return (nabla_b, nabla_w)

4.完整代码实现

# -*- coding: utf-8 -*-

import random
import numpy as np

class Network(object):

  def __init__(self, sizes):
  """参数sizes表示每一层神经元的个数，如[2,3,1],表示第一层有2个神经元，第二层有3个神经元，第三层有1个神经元."""
    self.num_layers = len(sizes)
    self.sizes = sizes
    self.biases = [np.random.randn(y, 1) for y in sizes[1:]]
    self.weights = [np.random.randn(y, x)
            for x, y in zip(sizes[:-1], sizes[1:])]

  def feedforward(self, a):
    """前向传播"""
    for b, w in zip(self.biases, self.weights):
      a = sigmoid(np.dot(w, a)+b)
    return a

  def SGD(self, training_data, epochs, mini_batch_size, eta,
      test_data=None):
    """随机梯度下降"""
    if test_data:
      n_test = len(test_data)
    n = len(training_data)
    for j in xrange(epochs):
      random.shuffle(training_data)
      mini_batches = [
        training_data[k:k+mini_batch_size]
        for k in xrange(0, n, mini_batch_size)]
      for mini_batch in mini_batches:
        self.update_mini_batch(mini_batch, eta)
      if test_data:
        print "Epoch {0}: {1} / {2}".format(j, self.evaluate(test_data), n_test)
      else:
        print "Epoch {0} complete".format(j)

  def update_mini_batch(self, mini_batch, eta):
    """使用后向传播算法进行参数更新.mini_batch是一个元组(x, y)的列表、eta是学习速率"""
    nabla_b = [np.zeros(b.shape) for b in self.biases]
    nabla_w = [np.zeros(w.shape) for w in self.weights]
    for x, y in mini_batch:
      delta_nabla_b, delta_nabla_w = self.backprop(x, y)
      nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
      nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
    self.weights = [w-(eta/len(mini_batch))*nw
            for w, nw in zip(self.weights, nabla_w)]
    self.biases = [b-(eta/len(mini_batch))*nb
            for b, nb in zip(self.biases, nabla_b)]

  def backprop(self, x, y):
    """返回一个元组(nabla_b, nabla_w)代表目标函数的梯度."""
    nabla_b = [np.zeros(b.shape) for b in self.biases]
    nabla_w = [np.zeros(w.shape) for w in self.weights]
    # 前向传播
    activation = x
    activations = [x] # list to store all the activations, layer by layer
    zs = [] # list to store all the z vectors, layer by layer
    for b, w in zip(self.biases, self.weights):
      z = np.dot(w, activation)+b
      zs.append(z)
      activation = sigmoid(z)
      activations.append(activation)
    # backward pass
    delta = self.cost_derivative(activations[-1], y) * sigmoid_prime(zs[-1])
    nabla_b[-1] = delta
    nabla_w[-1] = np.dot(delta, activations[-2].transpose())
    """l = 1 表示最后一层神经元，l = 2 是倒数第二层神经元, 依此类推."""
    for l in xrange(2, self.num_layers):
      z = zs[-l]
      sp = sigmoid_prime(z)
      delta = np.dot(self.weights[-l+1].transpose(), delta) * sp
      nabla_b[-l] = delta
      nabla_w[-l] = np.dot(delta, activations[-l-1].transpose())
    return (nabla_b, nabla_w)

  def evaluate(self, test_data):
    """返回分类正确的个数"""
    test_results = [(np.argmax(self.feedforward(x)), y) for (x, y) in test_data]
    return sum(int(x == y) for (x, y) in test_results)

  def cost_derivative(self, output_activations, y):
    return (output_activations-y)

def sigmoid(z):
  return 1.0/(1.0+np.exp(-z))

def sigmoid_prime(z):
  """sigmoid函数的导数"""
  return sigmoid(z)*(1-sigmoid(z))

5.简单应用

# -*- coding: utf-8 -*-

from network import *

def vectorized_result(j,nclass):
  """离散数据进行one-hot"""
  e = np.zeros((nclass, 1))
  e[j] = 1.0
  return e

def get_format_data(X,y,isTest):
  ndim = X.shape[1]
  nclass = len(np.unique(y))
  inputs = [np.reshape(x, (ndim, 1)) for x in X]
  if not isTest:
    results = [vectorized_result(y,nclass) for y in y]
  else:
    results = y
  data = zip(inputs, results)
  return data

#随机生成数据
from sklearn.datasets import *
np.random.seed(0)
X, y = make_moons(200, noise=0.20)
ndim = X.shape[1]
nclass = len(np.unique(y))

#划分训练、测试集
from sklearn.cross_validation import train_test_split
train_x,test_x,train_y,test_y = train_test_split(X,y,test_size=0.2,random_state=0)

training_data = get_format_data(train_x,train_y,False)
test_data = get_format_data(test_x,test_y,True)

net = Network(sizes=[ndim,10,nclass])
net.SGD(training_data=training_data,epochs=5,mini_batch_size=10,eta=0.1,test_data=test_data)

参考文献
（1）周志华《机器学习》
（2）https://github.com/mnielsen/neural-networks-and-deep-learning
（3）https://zhuanlan.zhihu.com/p/21525237

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持我们。