java为什么会出现精度丢失这种现象你知道吗

目录
  • 1.二进制转十进制
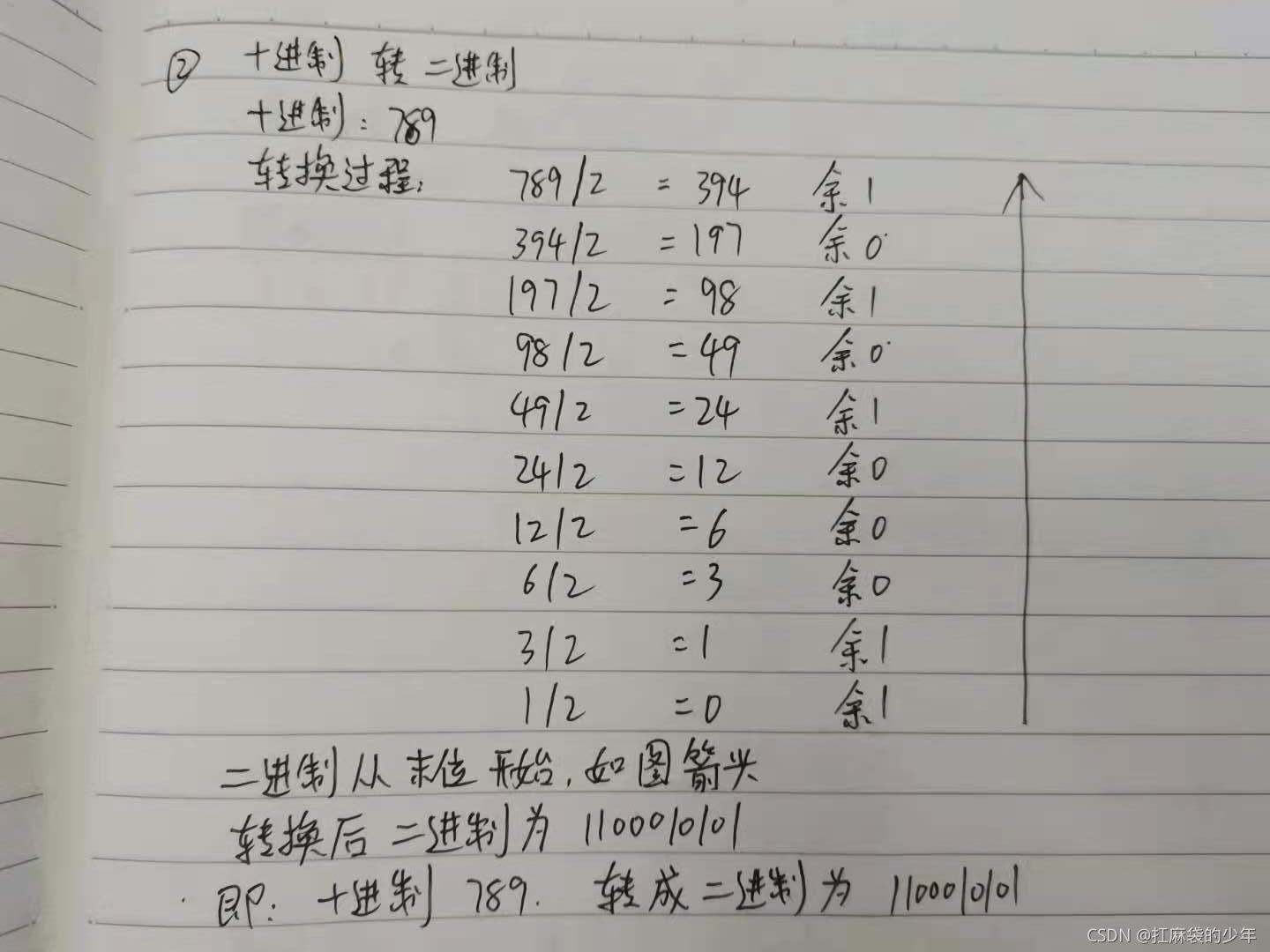
  • 2.(整数)十进制转二进制
  • 3.(小数)十进制转二进制(可除尽)
  • 4.(小数)十进制转二进制(除不尽)
  • 总结：  

很多人都知道：浮点数值不适用于无法接受舍入误差的金融计算中，即：我们常说的丢失精度问题。

这是为什么呢？

很多人还知道这样一句话：这种舍入误差的主要原因是浮点数值采用二进制系统表示， 而在二进制系统中无法精确地表示分数 1/10。这就好像十进制无法精确地表示分数 1/3—样。

针对十进制，1除以3是除不尽的。很好理解，因为我们一直接触的就是十进制，等于0.333333… 很好理解

但是：二进制系统中无法精确地表示分数 1/10。为啥呢。就有点不理解了

《Java核心技术卷》书上也是这么写的。

接下来我们就深究一下为什么！！！ 

重点这句话：这种舍入误差的主要原因是浮点数值采用二进制系统表示。就是说我们在代码中编写的 System.out.println(4.0 - 3.6); 这样一段代码， 

计算过程：

①将十进制的 4.0 转换成 二进制，将十进制的 3.6 转换成二进制；

②使用转换后的二进制，进行减法运算 

3.6 转换成二进制，就类似于 1除以3一样，是除不尽。所以 System.out.println(4.0 - 3.6); 就会输出 0.3999999999999999

备注：

十进制的 3.6 转换成二进制为：11.100110011001…(一直循环除不尽)，就类似于 1/3 是 0.33333333333…除不尽。所以System.out.println(4.0 - 3.6); 就会输出 0.3999999999999999

十进制的 3.6 转换成二进制为：11.100110011001…

转换过程参考下文⬇⬇⬇ 【4.(小数)十进制转二进制(除不尽)】

此处涉及到进制转换，参考下文：

涉及到：

1.二进制 转 十进制
2.十进制 转 二进制
3.(小数)十进制 转 二进制

接下来，举几个二进制和十进制之间转换的例子 。你就知道为什么【除不尽】了

1.二进制转十进制

2.(整数)十进制转二进制

3.(小数)十进制转二进制(可除尽)

4.(小数)十进制转二进制(除不尽)

总结：  

因为 3.6 转成二进制为 11.10011001....，除不尽的

所以 System.out.println(4.0 - 3.6); 就会输出 0.3999999999999999

本片文章就到这里了，希望能够给你带来帮助，也希望您能够多多关注我们的更多内容！

赞 (0)

相关推荐

  • Java用BigDecimal类解决Double类型精度丢失的问题

    Java用BigDecimal类解决Double类型精度丢失的问题

    本篇要点 简单描述浮点数十进制转二进制精度丢失的原因. 介绍几种创建BigDecimal方式的区别. 整理了高精度计算的工具类. 学习了阿里巴巴Java开发手册关于BigDecimal比较相等的规定. 经典问题:浮点数精度丢失 精度丢失的问题是在其他计算机语言中也都会出现,float和double类型的数据在执行二进制浮点运算的时候,并没有提供完全精确的结果.产生误差不在于数的大小,而是因为数的精度. 关于浮点数存储精度丢失的问题,话题过于庞大,感兴趣的同学可以自行搜索一下:[解惑]剖析floa

  • gson ajax 数字精度丢失问题的解决方法

    ajax传输的json,gson会发生丢失,long > 15的时候会丢失0 解决方案:直接把属性为long的属性自动加上双引号成为js的字符串,这样就不会发生丢失了,ajax自动识别为字符串. 用法: ajaxResult("",0,new Object()); //随便一个对象就可以,List 之类的 /** * 以Ajax方式输出常规操作结果 * * @param status * 返回状态,200表示成功, 500表示错误 * @param message * 操作结果描

  • 解决java数值范围以及float与double精度丢失的问题

    1.java中int,float,long,double取值范围 public class TestOutOfBound { public static void main(String[] args) { System.out.println(Integer.MAX_VALUE-(-Integer.MAX_VALUE)); //内存溢出 System.out.println(Integer.MAX_VALUE); //2的31次方-1,10个数位,正的20亿左右,用在钱上面不一定够 Syste

  • JS大坑之19位数的Number型精度丢失问题详解

    JS大坑之19位数的Number型精度丢失问题详解

    More 本项目仅供爬取体验,每次访问都会实时爬取数据,所以数据返回速度会比较慢,实际操作应该是定时爬取数据然后将数据存进数据库,数据从数据库返回从而提高数据返回效率. 但项目很基础,可以作为以上各个node模块最基础的练手使用,希望可以帮到大家

  • java为什么会出现精度丢失这种现象你知道吗

    java为什么会出现精度丢失这种现象你知道吗

    目录 1.二进制转十进制 2.(整数)十进制转二进制 3.(小数)十进制转二进制(可除尽) 4.(小数)十进制转二进制(除不尽) 总结:   很多人都知道:浮点数值不适用于无法接受舍入误差的金融计算中,即:我们常说的丢失精度问题. 这是为什么呢? 很多人还知道这样一句话:这种舍入误差的主要原因是浮点数值采用二进制系统表示, 而在二进制系统中无法精确地表示分数 1/10.这就好像十进制无法精确地表示分数 1/3-样. 针对十进制,1除以3是除不尽的.很好理解,因为我们一直接触的就是十进制,等于0.

  • 浅谈JavaScript中小数和大整数的精度丢失

    先来看两个问题: 0.1 + 0.2 == 0.3; // false 9999999999999999 == 10000000000000000; // true 第一个问题是小数的精度问题,在业界不少博客里已有讨论.第二个问题,去年公司有个系统的数据库在做数据订正时,发现有部分数据重复的诡异现象.本文将从规范出发,对上面的问题做个小结. 最大整数 JavaScript 中的数字是用 IEEE 754 双精度 64 位浮点数 来存储的,其格式为: s x m x 2^e s 是符号位,表示正负

  • 解决JavaScript数字精度丢失问题的方法

    解决JavaScript数字精度丢失问题的方法

    本文分为三个部分 JS 数字精度丢失的一些典型问题 JS 数字精度丢失的原因 解决方案(一个对象+一个函数) 一.JS数字精度丢失的一些典型问题 1. 两个简单的浮点数相加 0.1 + 0.2 != 0.3 // true 这真不是 Firebug 的问题,可以用alert试试 (哈哈开玩笑). 看看Java的运算结果 再看看Python 2. 大整数运算 16位和17位数竟然相等,没天理啊. 又如 var x = 9007199254740992 x + 1 == x // ? 看结果 三观又

  • javascript解决小数的加减乘除精度丢失的方案

    javascript解决小数的加减乘除精度丢失的方案

    原因:js按照2进制来处理小数的加减乘除,在arg1的基础上 将arg2的精度进行扩展或逆扩展匹配,所以会出现如下情况. javascript(js)的小数点加减乘除问题,是一个js的bug如0.3*1 = 0.2999999999等,下面列出可以完美求出相应精度的四种js算法 function accDiv(arg1,arg2){ var t1=0,t2=0,r1,r2; try{t1=arg1.toString().split(".")[1].length}catch(e){} t

  • java double类型相加精度问题的解决

    我就废话不多说了,大家还是直接看代码吧~ package com.hxyl.action; import java.text.DecimalFormat; public class Test { public static void main(String[] args) { // DecimalFormat 类主要靠 # 和 0 两种占位符号来指定数字长度.0 表示如果位数不足则以 0 填充,# 会把最后面的零默认省略. DecimalFormat df = new DecimalFormat

  • 解析Spring Mvc Long类型精度丢失问题

    解析Spring Mvc Long类型精度丢失问题

    背景 在使用Spring Boot Mvc的项目中,使用Long类型作为id的类型,但是当前端使用Number类型接收Long类型数据时,由于前端精度问题,会导致Long类型数据转换为Number类型时的后两位变为0 Spring Boot Controller 以下代码提供一个Controller,返回一个Dto, Dto的id是Long类型的,其中id的返回数据是1234567890102349123 @CrossOrigin 注解表示可以跨域访问 @RestController() @Re

  • C语言中浮点数的精度丢失问题解决

    C语言中浮点数的精度丢失问题解决

    目录 一 先来看一段代码 运行结果: 二 如何解决 (1)浮点数的大小比较 (2)含浮点数的表达式和0.0的比较 总结 一 先来看一段代码 #include<stdio.h> int main() { double test=0.1; printf("%.100lf",test); return 0; } 运行结果: 直接从现象说结果:精度丢失由于计算机二进制转化过程中因为比特位过多发生数据的截断导致的,这个结果是可以偏大也可以偏小的. 解释一下:首先要知道二进制转换为十进

随机推荐