python实现PCA降维的示例详解

概述

本文主要介绍一种降维方法，PCA（Principal Component Analysis，主成分分析）。降维致力于解决三类问题。

1. 降维可以缓解维度灾难问题；

2. 降维可以在压缩数据的同时让信息损失最小化；

3. 理解几百个维度的数据结构很困难，两三个维度的数据通过可视化更容易理解。

PCA简介

在理解特征提取与处理时，涉及高维特征向量的问题往往容易陷入维度灾难。随着数据集维度的增加，算法学习需要的样本数量呈指数级增加。有些应用中，遇到这样的大数据是非常不利的，而且从大数据集中学习需要更多的内存和处理能力。另外，随着维度的增加，数据的稀疏性会越来越高。在高维向量空间中探索同样的数据集比在同样稀疏的数据集中探索更加困难。

主成分分析也称为卡尔胡宁-勒夫变换（Karhunen-Loeve Transform），是一种用于探索高维数据结构的技术。PCA通常用于高维数据集的探索与可视化。还可以用于数据压缩，数据预处理等。PCA可以把可能具有相关性的高维变量合成线性无关的低维变量，称为主成分（ principal components）。新的低维数据集会尽可能的保留原始数据的变量。

PCA将数据投射到一个低维子空间实现降维。例如，二维数据集降维就是把点投射成一条线，数据集的每个样本都可以用一个值表示，不需要两个值。三维数据集可以降成二维，就是把变量映射成一个平面。一般情况下，nn维数据集可以通过映射降成kk维子空间，其中k≤nk≤n。

假如你是一本养花工具宣传册的摄影师，你正在拍摄一个水壶。水壶是三维的，但是照片是二维的，为了更全面的把水壶展示给客户，你需要从不同角度拍几张图片。下图是你从四个方向拍的照片：

第一张图里水壶的背面可以看到，但是看不到前面。第二张图是拍前面，可以看到壶嘴，这张图可以提供了第一张图缺失的信息，但是壶把看不到了。从第三张俯视图里无法看出壶的高度。第四张图是你真正想要的，水壶的高度，顶部，壶嘴和壶把都清晰可见。

PCA的设计理念与此类似，它可以将高维数据集映射到低维空间的同时，尽可能的保留更多变量。PCA旋转数据集与其主成分对齐，将最多的变量保留到第一主成分中。假设我们有下图所示的数据集：

数据集看起来像一个从原点到右上角延伸的细长扁平的椭圆。要降低整个数据集的维度，我们必须把点映射成一条线。下图中的两条线都是数据集可以映射的，映射到哪条线样本变化最大？

显然，样本映射到黑色虚线的变化比映射到红色点线的变化要大的多。实际上，这条黑色虚线就是第一主成分。第二主成分必须与第一主成分正交，也就是说第二主成分必须是在统计学上独立的，会出现在与第一主成分垂直的方向，如下图所示：

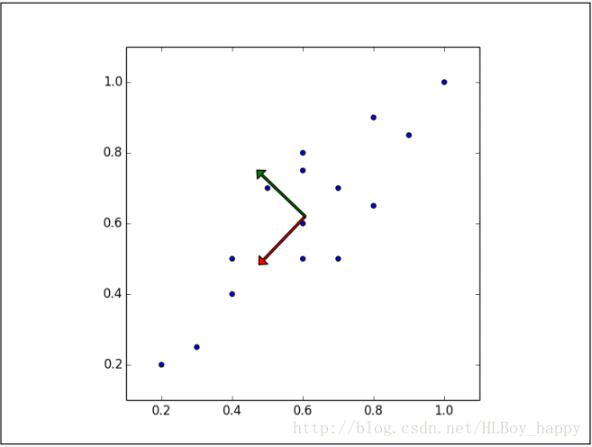
后面的每个主成分也会尽量多的保留剩下的变量，唯一的要求就是每一个主成分需要和前面的主成分正交。

现在假设数据集是三维的，散点图看起来像是沿着一个轴旋转的圆盘。

这些点可以通过旋转和变换使圆盘完全变成二维的。现在这些点看着像一个椭圆，第三维上基本没有变量，可以被忽略。

当数据集不同维度上的方差分布不均匀的时候，PCA最有用。（如果是一个球壳形数据集，PCA不能有效的发挥作用，因为各个方向上的方差都相等；没有丢失大量的信息维度一个都不能忽略）。

python实现PCA降维代码 

# coding=utf-8
from sklearn.decomposition import PCA
from pandas.core.frame import DataFrame
import pandas as pd
import numpy as np
l=[]
with open('test.csv','r') as fd:

  line= fd.readline()
  while line:
    if line =="":
      continue

    line = line.strip()
    word = line.split(",")
    l.append(word)
    line= fd.readline()

data_l=DataFrame(l)
print (data_l)
dataMat = np.array(data_l) 

pca_sk = PCA(n_components=2)
newMat = pca_sk.fit_transform(dataMat) 

data1 = DataFrame(newMat)
data1.to_csv('test_PCA.csv',index=False,header=False)

以上这篇python实现PCA降维的示例详解就是小编分享给大家的全部内容了，希望能给大家一个参考，也希望大家多多支持我们。

赞 (0)

相关推荐

  • python实现拉普拉斯特征图降维示例

    这种方法假设样本点在光滑的流形上,这一方法的计算数据的低维表达,局部近邻信息被最优的保存.以这种方式,可以得到一个能反映流形的几何结构的解. 步骤一:构建一个图G=(V,E),其中V={vi,i=1,2,3-n}是顶点的集合,E={eij}是连接顶点的vi和vj边,图的每一个节点vi与样本集X中的一个点xi相关.如果xi,xj相距较近,我们就连接vi,vj.也就是说在各自节点插入一个边eij,如果Xj在xi的k领域中,k是定义参数. 步骤二:每个边都与一个权值Wij相对应,没有连接点之间的权值为

  • python数据预处理方式 :数据降维

    python数据预处理方式 :数据降维

    数据为何要降维 数据降维可以降低模型的计算量并减少模型运行时间.降低噪音变量信息对于模型结果的影响.便于通过可视化方式展示归约后的维度信息并减少数据存储空间.因此,大多数情况下,当我们面临高维数据时,都需要对数据做降维处理. 数据降维有两种方式:特征选择,维度转换 特征选择 特征选择指根据一定的规则和经验,直接在原有的维度中挑选一部分参与到计算和建模过程,用选择的特征代替所有特征,不改变原有特征,也不产生新的特征值. 特征选择的降维方式好处是可以保留原有维度特征的基础上进行降维,既能满足后续数据

  • python 列表降维的实例讲解

    列表降维(python:3.x) 之前遇到需要使用列表降维的情况, 如: 原列表 : [[12,34],[57,86,1],[43,22,7],[1,[2,3]],6] 转化为 : [12, 34, 57, 86, 1, 43, 22, 7, 1, 2, 3, 6] 思路: 把列表转化为字符串,直接去掉 "[" 和 "]" 最后由字符串转化为列表 a = [[12,34],[57,86,1],[43,22,7],[1,[2,3]],6] #把列表转为字符串 b =

  • python实现PCA降维的示例详解

    概述 本文主要介绍一种降维方法,PCA(Principal Component Analysis,主成分分析).降维致力于解决三类问题. 1. 降维可以缓解维度灾难问题: 2. 降维可以在压缩数据的同时让信息损失最小化: 3. 理解几百个维度的数据结构很困难,两三个维度的数据通过可视化更容易理解. PCA简介 在理解特征提取与处理时,涉及高维特征向量的问题往往容易陷入维度灾难.随着数据集维度的增加,算法学习需要的样本数量呈指数级增加.有些应用中,遇到这样的大数据是非常不利的,而且从大数据集中学习

  • Python线性点运算数字图像处理示例详解

    Python线性点运算数字图像处理示例详解

    目录 点运算 定义 分类 线性点运算 分段线性点运算 非线性点运算 对数变换 幂次变换 点运算 定义 分类 线性点运算 例子: 分段线性点运算 非线性点运算 对数变换 幂次变换 1. 点运算是否会改变图像内像素点之间的空间位置关系? 点运算是一种像素的逐点运算,它与相邻的像素之间没有运算关系,点运算不会改变图像内像素点之间的空间位置关系. 2. 对图像灰度的拉伸,非线性拉伸与分段线性拉伸的区别? 非线性拉伸不是通过在不同灰度值区间选择不同的线性方程来实现对不同灰度值区间的扩展与压缩,而是在整个灰

  • Python面向对象编程repr方法示例详解

    目录 为什么要讲 __repr__ 重写 __repr__ 方法 str() 和 repr() 的区别 为什么要讲 __repr__ 在 Python 中,直接 print 一个实例对象,默认是输出这个对象由哪个类创建的对象,以及在内存中的地址(十六进制表示) 假设在开发调试过程中,希望使用 print 实例对象时,输出自定义内容,就可以用 __repr__ 方法了 或者通过 repr() 调用对象也会返回 __repr__ 方法返回的值 是不是似曾相识....没错..和 __str__ 一样的

  • python函数传参意义示例详解

    python函数传参意义示例详解

    目录 C++这样的语言用多了之后,在Python函数传递参数的时候,经常会遇到一个问题,我要传递一个引用怎么办? 比如我们想要传一个x到函数中做个运算改变x的值: def change(y): y += 1 x = 1 print ("before change:", x) change(x) print ("after change: ", x) 得到的结果是 before change: 1 after change:  1 完全没用~~~这是怎么回事? 我来说

  • python模块shutil函数应用示例详解教程

    python模块shutil函数应用示例详解教程

    目录 本文大纲 知识串讲 1)模块导入 2)复制文件 3)复制文件夹 4)移动文件或文件夹 5)删除文件夹(慎用) 6)创建和解压压缩包 本文大纲 os模块是Python标准库中一个重要的模块,里面提供了对目录和文件的一般常用操作.而Python另外一个标准库--shutil库,它作为os模块的补充,提供了复制.移动.删除.压缩.解压等操作,这些 os 模块中一般是没有提供的.但是需要注意的是:shutil 模块对压缩包的处理是调用 ZipFile 和 TarFile这两个模块来进行的. 知识串

  • Python实现连接dr校园网示例详解

    Python实现连接dr校园网示例详解

    目录 背景 分析 实现 背景 在校园里认证上网很麻烦需要web输入账号密码有时还会忘记web地址此时就需要一个人或者程序帮我们实现,这时我想到用python制作这个程序(初学者python代码不规范) 分析 需要分析web登录网址的浏览器头发现是get方法这就简单了,再次分析get请求发现有user_account字段,user_password字段还有ip字段mac字段这时我们的思路就来了使用curl命令直接把这个代码放到终端里运行发现是可以的 curl "http://学校认证服务器ip:8

  • Python绘制3D立体花朵示例详解

    Python绘制3D立体花朵示例详解

    目录 动态展示 导读 源码和详解 荷花 玫瑰花 桃花 月季 动态展示 这是一个动态图哦 导读 兄弟们可以收藏一下哦!情人节可以送出去,肥学找了几朵python写的花给封装好送给大家.不是多炫酷但是有足够的用心哦.别忘了点赞呀我也就不细说了,来吧展示! 源码和详解 荷花 def lotus(): fig = plt.figure(figsize=(10,7),facecolor='black',clear=True) ax = fig.gca(projection='3d') [x, t] = n

  • Python+matplotlib实现绘制等高线图示例详解

    Python+matplotlib实现绘制等高线图示例详解

    目录 前言 1. 等高线图概述 什么是等高线图? 等高线图常用场景 绘制等高线图步骤 案例展示 2. 等高线图属性 设置等高线颜色 设置等高线透明度 设置等高线颜色级别 设置等高线宽度 设置等高线样式 3. 显示轮廓标签 4. 填充颜色 5. 添加颜色条说明 总结 前言 我们在往期对matplotlib.pyplot()方法学习,到现在我们已经会绘制折线图.柱状图.散点等常规的图表啦(往期的内容如下,大家可以方便查看往期内容) Python matplotlib底层原理解析 Python利用 m

  • Python制作可视化报表的示例详解

    Python制作可视化报表的示例详解

    大家好,我是小F- 在数据展示中使用图表来分享自己的见解,是个非常常见的方法. 这也是Tableau.Power BI这类商业智能仪表盘持续流行的原因之一,这些工具为数据提供了精美的图形解释. 当然了,这些工具也有着不少缺点,比如不够灵活,无法让你自己创建设计. 当你对图表展示要求定制化时,编程也许就比较适合你,比如Echarts.D3.js. 今天小F给大家介绍一个用Python制作可视化报表的案例,主要是使用到Dash+Tailwindcss. 可视化报表效果如下,水果销售情况一览~ Das

  • Python学习之模块化程序设计示例详解

    Python学习之模块化程序设计示例详解

    目录 关于模块化程序设计 水果仓库功能简介 主功能实现与程序入口 实现添加功能 实现列出所有信息功能 实现查询信息功能 实现删除信息功能 完整程序如下 关于模块化程序设计 什么是模块化程序设计? 程序设计的模块化指的是在进行程序设计时,把一个大的程序功能划分为若干个小的程序模块.每一个小程序模块实现一个确定的功能,并且在这些小程序模块实现的功能之间建立必要的联系,通过各个小模块之间的互相协作完成整个大功能实现的方法. 模块化设计程序的方法? 一般在针对实现比较复杂程序的情况下,采用的是自上而下的

随机推荐