关于背包问题的一些理解和应用
1.背包问题介绍
背包问题不单单是一个简单的算法问题,它本质上代表了一大类问题,这类问题实际上是01线性规划问题,其约束条件和目标函数如下:
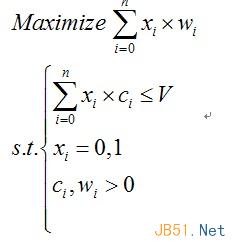
自从dd_engi在2007年推出《背包问题九讲》之后,背包问题的主要精髓基本已道尽。本文没有尝试对背包问题的本质进行扩展或深入挖掘,而只是从有限的理解(这里指对《背包问题九讲》的理解)出发,帮助读者更快地学习《背包问题九讲》中的提到的各种背包问题的主要算法思想,并通过实例解释了相应的算法,同时给出了几个背包问题的经典应用。
2.背包问题及应用
dd_engi在《背包问题九讲》中主要提到四种背包问题,分别为:01背包问题,完全背包问题,多重背包问题,二维费用背包问题。本节总结了这几种背包问题,并给出了其典型的应用以帮助读者理解这几种问题的本质。
2.101背包问题
(1)问题描述
有N件物品和一个容量为V的背包。第i件物品的费用是c[i],价值是w[i]。求解将哪些物品装入背包可使价值总和最大。
(2)状态转移方程

其中,f(i,v) 表示从前i件物品选择若干物品装到容量为v的背包中产生的最大价值。当v=0时,f(i,v)初始化为0,表示题目不要求背包一定刚好装满,而f(i,v)=inf/-inf(正无穷或负无穷)表示题目要求背包一定要刚好装满。下面几种背包类似,以后不再赘述。
(3) 伪代码
从转移方程上可以看出,前i个物品的最优解只依赖于前i-1个物品最优解,而与前i-2,i-3,…各物品最优无直接关系,可以利用这个特点优化存储空间,即只申请一个一维数组即可,算法时间复杂度(O(VN))为:
for i=1..N
for v=V..0
f[v]=max{f[v],f[v-c[i]]+w[i]};
注意v的遍历顺序!!!
下面几种背包用到类似优化,以后不再赘述。
(4) 举例
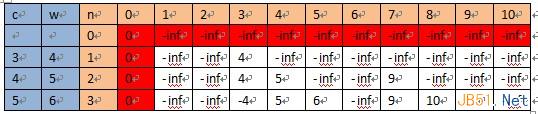
V=10,N=3,c[]={3,4,5}, w={4,5,6}
(1)背包不一定装满
计算顺序是:从右往左,自上而下:
(2)背包刚好装满
计算顺序是:从右往左,自上而下。注意初始值,其中-inf表示负无穷
(5) 经典题型
[1] 你有一堆石头质量分别为W1,W2,W3…WN.(W<=100000,N <30)现在需要你将石头合并为两堆,使两堆质量的差为最小。
[2] 给一个整数的集合,要把它分成两个集合,要两个集合的数的和最接近
[3] 有一个箱子容量为V(正整数,0≤V≤20000),同时有n个物品(0小于n≤30),每个物品有一个体积(正整数)。要求从n个物品中,任取若干个装入箱内,使箱子的剩余空间为最小。
2.2完全背包问题
(1)问题描述
有N种物品和一个容量为V的背包,每种物品都有无限件可用。第i种物品的费用是c[i],价值是w[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量,且价值总和最大。
(2)状态转移方程
 或者:
或者:

(3) 伪代码
for i=1..N
for v=0..V
f[v]=max{f[v],f[v-c[i]]+w[i]};
注意v的遍历顺序!!!
注意,时间复杂度仍为:O(VN).
(4) 举例
V=10,N=3,c[]={3,4,5}, w={4,5,6}
(1)背包不一定装满
计算顺序是:从左往右,自上而下:
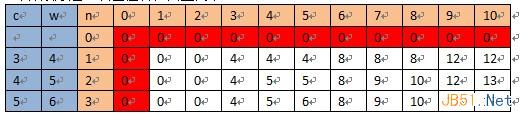
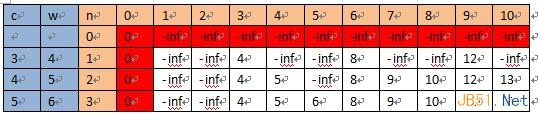
(2)背包刚好装满
计算顺序是:从左往右,自上而下。注意初始值,其中-inf表示负无穷
(5) 经典题型
[1] 找零钱问题:有n种面额的硬币,每种硬币无限多,至少用多少枚硬币表示给定的面值M?
2.3多重背包问题
(1)问题描述
有N种物品和一个容量为V的背包。第i种物品最多有n[i]件可用,每件费用是c[i],价值是w[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量,且价值总和最大。
(2)状态转移方程

(3) 解题思想
用以下方法转化为普通01背包问题:将第i种物品分成若干件物品,其中每件物品有一个系数,这件物品的费用和价值均是原来的费用和价值乘以这个系数。使这些系数分别为 1,2,4,…,2^(k-1),n[i]-2^k+1,且k是满足n[i]-2^k+1>0的最大整数。例如,如果n[i]为13,就将这种 物品分成系数分别为1,2,4,6的四件物品。这种方法能保证对于0..n[i]间的每一个整数,均可以用若干个系数的和表示。这个很容易证明,证明过程中用到以下定理:任何一个整数n均可以表示成:n=a0*2^0+a1*2^1+…+ak*2^k,其中ak=0或者1(实际上就是n的二进制分解),
定理:一个正整数n可以被分解成1,2,4,…,2^(k-1),n-2^k+1(k是满足n-2^k+1>0的最大整数)的形式,且1~n之内的所有整数均可以唯一表示成1,2,4,…,2^(k-1),n-2^k+1中某几个数的和的形式。
该定理的证明如下:
(1) 数列1,2,4,…,2^(k-1),n-2^k+1中所有元素的和为n,所以若干元素的和的范围为:[1, n];
(2)如果正整数t<= 2^k – 1,则t一定能用1,2,4,…,2^(k-1)中某几个数的和表示,这个很容易证明:我们把t的二进制表示写出来,很明显,t可以表示成n=a0*2^0+a1*2^1+…+ak*2^(k-1),其中ak=0或者1,表示t的第ak位二进制数为0或者1.
(3)如果t>=2^k,设s=n-2^k+1,则t-s<=2^k-1,因而t-s可以表示成1,2,4,…,2^(k-1)中某几个数的和的形式,进而t可以表示成1,2,4,…,2^(k-1),s中某几个数的和(加数中一定含有s)的形式。
(证毕!)
该算法的时间复杂度为:O(V*sum(logn[i])).
(4) 经典题型
[1] 找零钱问题:有n种面额的硬币,分别为a[0], a[1],…, a[n-1],每种硬币的个数为b[0], b[1],…, b[n-1],至少用多少枚硬币表示给定的面值M?
2.4二维费用背包
(1)问题描述
二维费用的背包问题是指:对于每件物品,具有两种不同的费用;选择这件物品必须同时付出这两种代价;对于每种代价都有一个可付出的最大值(背包容量)。问 怎样选择物品可以得到最大的价值。设这两种代价分别为代价1和代价2,第i件物品所需的两种代价分别为a[i]和b[i]。两种代价可付出的最大值(两种 背包容量)分别为V和U。物品的价值为w[i]。
(2)状态转移方程
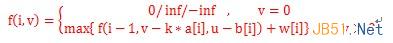
(3)算法思想
采用同一维情况类似的方法求解
(4)经典题型
有2n个整数,平均分成两组,每组n个数,使这两组数的和最接近。
3.背包总结
背包问题实际上代表的是线性规划问题,一般要考虑以下几个因素已决定选取什么样的算法:
(1)约束条件,有一个还是两个或者更多个,如果是一个,可能是01背包,完全背包或者多重背包问题,如果有两个约束条件,则可能是二维背包问题。
(2)优化目标,求最大值,还是最小值,还是总数(只需将max换成sum)
(3)每种物品的个数限制,如果每种物品只有一个,只是简单的01背包问题,如果个数无限制,则是完全背包问题,如果每种物品的个数有限制,则是多重背包问题。
(4)背包是否要求刚好塞满,注意不塞满和塞满两种情况下初始值不同。
4.参考资料
dd_engi:《背包问题九讲》

