详解Java中跳跃表的原理和实现

目录

• 一、跳跃表的引入
• 二、算法分析
• 1.时间复杂度
• 2.空间复杂度
• 三、跳跃表介绍
• 四、跳跃表的实现
• 1.数据结构定义
• 2.查找
• 3.插入
• 4.删除
• 五、实战
• 1.代码
• 2.测试结果

一、跳跃表的引入

对有序顺序表可以采用二分查找，查找的时间复杂度为O (logn)，插入、删除的时间复杂度为 O(n )。但是对有序链表不可以采用二分查找，查找、插入和删除的时间复杂度均为O (n)。

有序链表如下图所示，若查找 8，则必须从第 1 个节点开始，依次比较 8 次才能查找成功。

如何利用链表的有序性来提高查找效率？如何在一个有序链表中进行二分查找？若增加一级索引，把奇数位序作为索引，则如下图所示，若查找 8，则可以先从索引进行比较，依次比较 1、3、5、7、9，8 比 7 大但比 9 小，7 向下一层，继续向后比较，比较 6 次即可查找成功。

若再增加一级索引，把索引层的奇数位序作为索引，则如下图所示，若查找 7，则可以先从索引开始比较，依次 1、5、9，7 比 5 大但比 9 小，5 向下一层，继续向后比较，比较 4 次即可查找成功。

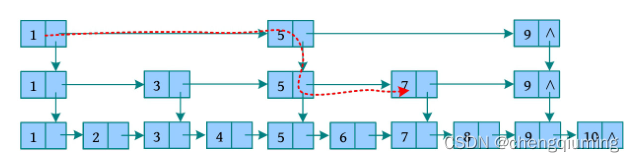
在增加两级索引后，若查找 5，则比较两次即可查找成功；若查找比 5 大的数，则以 5 为界向后查找；若查找比 5 小的数，则以 5 为界向前查找。这就是一个可进行二分查找的有序链表。

二、算法分析

若有 n 个元素，则增加 h 级索引后的数据结构如下图所示。

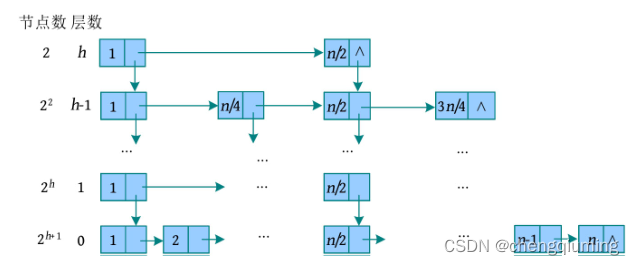
1.时间复杂度

底层包含所有元素（n个），即 2^(h +1)=n ，索引层数 h=logn-1。搜索时，首先在顶层索引中进行查找，然后二分搜索，最多从顶层搜索到底层，最多 O(logn) 层，因此查找的时间复杂度为 O(logn)。

2.空间复杂度

增加索引需要一些辅助空间，那么索引一共有多少个节点呢？从上图中可以看出，每层索引的节点之和都为 2+2^2 +…+2^h =2^(h +1)-2=n-2，因此空间复杂度为 O(n )。实际上，索引节点并不是原节点的复制，只是附加了一些指针建立索引。以上正是跳跃表的实现原理。

三、跳跃表介绍

跳跃表（Skip list）是有序链表的扩展，简称跳表，它在原有的有序链表上增加了多级索引，通过索引来实现快速查找，实质上是一种可以进行二分查找的有序链表。

实际上，跳跃表并不是简单地通过奇偶次序建立索引的，而是通过随机技术实现的，因此也可以说它是一种随机化的数据结构。假如跳跃表每一层的晋升概率都是 1/2，则最理想的索引就是在原始链表中每隔一个元素抽取一个元素作为一级索引。其实在原始链表中随机选择 n/2 个元素作为一级索引也可以，因为随机选择的元素相对均匀，对查找效率来讲影响不大。当原始链表中元素数量足够大且抽取足够随机时，得到的索引是均匀的。因此随机选择 n/2 个元素作为一级索引，随机选择 n/4 个元素作为二级索引，随机选择 n/8 个元素作为三级索引，以此类推，一直到顶层索引。我们可以通过索引来提升跳跃表的查找效率。

跳跃表不仅可以提高搜索性能，还可以提高插入和删除操作的性能。平衡二叉查找树在进行插入、删除操作后需要多次调整平衡，而跳跃表完全依靠随机技术，其性能和平衡二叉查找树不相上下，但是原理非常简单。跳跃表是一种性能比较优秀的动态数据结构，Redis 中的有序集合 Sorted Set 和 LevelDB 中的 MemTable 都是采用跳跃表实现的。

四、跳跃表的实现

1.数据结构定义

在每个节点都可以设置向右、向下指针，当然，也可以附加向左、向上指针，构建四联表。通过四联表可以快速地在四个方向访问前驱和后继。在此仅设置向右指针，在每个节点都定义一个后继指针数组，通过层次控制向下访问。

2.查找

在跳跃表中查找元素 x ，需要从最上层索引开始逐层查找，算法步骤如下。

（1）从最上层 Sh 的头节点开始。

（2）假设当前位置为 p ，p 的后继节点的值为 y ，若 x=y，则查找成功；若 x>y ，则 p 向后移一个位置，继续查找；若 x<y ，则 p 向下移动一个位置，继续查找。

（3）若到达底层还要向下移动，则查找失败。

例如，跳跃表如下图所示，在表中查找元素 36，则先从顶层的头节点开始，比 20 大，向后为空，p 向下移动到第 2 层；比下一个元素 50 小，p 向下移动到第 1 层；比下一个元素 30 大，p 向右移动；比下一个元素 50 小，p 向下移动到第 0 层；与下一个元素 36 比较，查找成功。

3.插入

在跳跃表中插入一个元素时，相当于在某一个位置插入一个高度为 level 的列。插入的位置可以通过查找确定，而插入列的高度可以采用随机化决策确定。

随机化获取插入元素的层次：

① 初始时 lay=0，可设定晋升概率P为 0.5 或 0.25。

② 利用随机函数产生 0～1的随机数 r。

④ 若 r 小于 P 且 lay 小于最大层次，则 lay+1；否则返回 lay，作为新插入元素的高度。

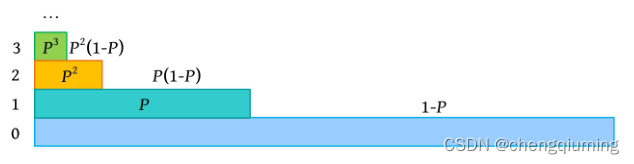
在跳跃表中插入元素的算法步骤如下。

（1）查找插入位置，在查找过程中用 updata[i] 记录经过的每一层的最大节点位置。

（2）采用随机化策略得到插入层次 lay。

（3）创建新节点，将高度为 lay 的列插入 updata[i] 之后。

例如，跳跃表如下图所示，在表中插入元素 32。首先在跳跃表中查找 32，然后确定插入位置。在查找过程中用 updata[i] 记录经过的每一层的最大节点位置；假设随机化得到的层次为 2，则 i 为 0～2，将新节点插入 updata[i] 之后。

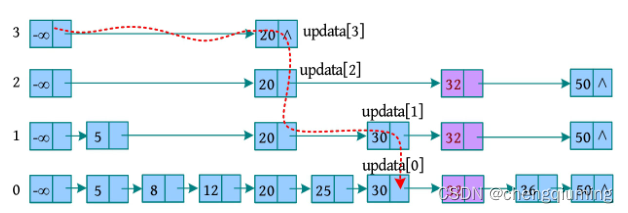
4.删除

在跳跃表中删除一个元素，相当于删除这个元素所在的列。

算法步骤：

（1）查找该元素，在查找过程中用 updata[i] 记录经过的每一层的最大节点位置，实际上是待删除节点在每一层的前一个元素的位置。若查找失败，则退出。

（2）利用 updata[i] 将该元素整列删除。

（3）若有多余空链，则删除空链。

例如，跳跃表如下图所示，在表中删除元素 20。首先在跳跃表中查找 20，在查找过程中用 updata[i] 记录经过的每一层的最大节点位置；然后利用 updata[i] 将每层的 20 节点删除。

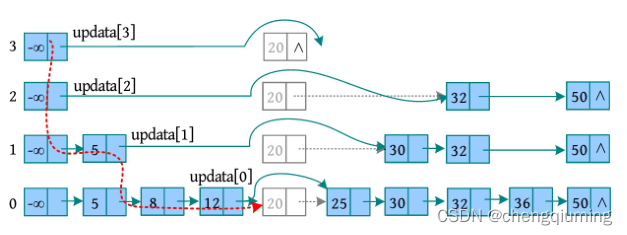
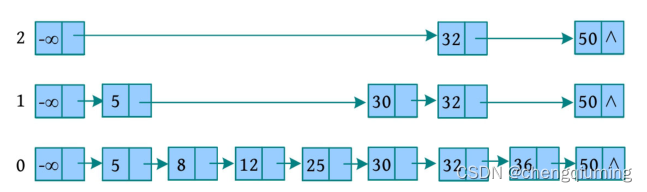
删除 20 所在的列后，最上层的链为空链，则删除空链，跳跃表的层次减 1。

五、实战

1.代码

package com.platform;

import java.util.Scanner;

public class SkipList {
    private static int INF = 0x7fffffff;
    private static float P = 0.5f;
    private static int MAX_LEVEL = 16;

    static class Node {
        int val;
        Node forward[] = new Node[MAX_LEVEL];
    }

    Node head = new Node();
    Node updata[] = new Node[MAX_LEVEL];

    public SkipList() {
        for (int i = 0; i < updata.length; i++) {
            updata[i] = new Node();
        }
    }

    void Init() {
        level = 0;
        head = new Node();
        for (int i = 0; i < MAX_LEVEL; i++)
            head.forward[i] = null;
        head.val = -INF;
    }

    // 随机产生插入元素高度
    static int RandomLevel() {
        int lay = 0;
        while ((float) Math.random() < P && lay < MAX_LEVEL - 1)
            lay++;
        return lay;
    }

    Node Find(int val) {//查找最接近val的元素
        Node p = head;
        for (int i = level; i >= 0; i--) {
            while (p.forward[i] != null && p.forward[i].val < val)
                p = p.forward[i];
            updata[i] = p;//记录搜索过程中各级走过的最大节点位置
        }
        return p;
    }

    void Insert(int val) {
        Node p, s;
        int lay = RandomLevel();
        System.out.printf("lay=%d\n", lay);
        if (lay > level) //要插入的层 > 现有层数
            level = lay;
        p = Find(val); //查询
        s = new Node();//创建一个新节点
        s.val = val;
        for (int i = 0; i < MAX_LEVEL; i++)
            s.forward[i] = null;
        for (int i = 0; i <= lay; i++) {//插入操作
            s.forward[i] = updata[i].forward[i];
            updata[i].forward[i] = s;
        }
    }

    void Delete(int val) {
        Node p = Find(val);
        if (p.forward[0] != null && p.forward[0].val == val) {
            System.out.printf("%d\n", p.forward[0].val);
            for (int i = level; i >= 0; i--) { // 删除操作
                if (updata[i].forward[i] != null && updata[i].forward[i].val == val)
                    updata[i].forward[i] = updata[i].forward[i].forward[i];
            }
            while (level > 0 && head.forward[level] == null) // 删除空链
                level--;
        }
    }

    void print(int i) { // 遍历
        Node p = head.forward[i];
        if (p == null) return;
        while (p != null) {
            System.out.printf("%d  ", p.val);
            p = p.forward[i];
        }
        System.out.printf("\n");
    }

    void printall() { // 遍历所有层
        for (int i = level; i >= 0; i--) {
            System.out.printf("level %d:  ", i);
            print(i);
        }
    }

    void show() {
        System.out.printf("Please select:\n");
        System.out.printf("-----------------------------\n");
        System.out.printf("     1:  插入\n");
        System.out.printf("     2:  删除\n");
        System.out.printf("     3:  查找\n");
        System.out.printf("     4:  遍历\n");
        System.out.printf("     5:  遍历所有层\n");
        System.out.printf("     0:  退出\n");
        System.out.printf("-----------------------------\n");
    }

    int level;

    public static void main(String[] args) {
        Scanner sn = new Scanner(System.in);
        SkipList skipList = new SkipList();
        skipList.Init();
        int n, x;
        skipList.show();
        while (true){
            n = sn.nextInt();
            switch (n) {
                case 1:
                    x = sn.nextInt();
                    skipList.Insert(x);
                    break;
                case 2:
                    x = sn.nextInt();
                    skipList.Delete(x);
                    break;
                case 3:
                    x = sn.nextInt();
                    Node p;
                    p = skipList.Find(x);
                    if (p.forward[0] != null && p.forward[0].val == x) {
                        System.out.printf("find success!\n");
                    } else {
                        System.out.printf("find fail!\n");
                    }

                    break;
                case 4:
                    skipList.print(0);
                    break;
                case 5:
                    skipList.printall();
                    break;
            }
            skipList.show();
        }
    }
}

2.测试结果

Please select:
-----------------------------
     1:  插入
     2:  删除
     3:  查找
     4:  遍历
     5:  遍历所有层
     0:  退出
-----------------------------
1
1
lay=0
Please select:
-----------------------------
     1:  插入
     2:  删除
     3:  查找
     4:  遍历
     5:  遍历所有层
     0:  退出
-----------------------------
5
level 0:  1  
Please select:
-----------------------------
     1:  插入
     2:  删除
     3:  查找
     4:  遍历
     5:  遍历所有层
     0:  退出
-----------------------------
1
4
lay=5
Please select:
-----------------------------
     1:  插入
     2:  删除
     3:  查找
     4:  遍历
     5:  遍历所有层
     0:  退出
-----------------------------
5
level 5:  4  
level 4:  4  
level 3:  4  
level 2:  4  
level 1:  4  
level 0:  1  4  
Please select:
-----------------------------
     1:  插入
     2:  删除
     3:  查找
     4:  遍历
     5:  遍历所有层
     0:  退出
-----------------------------
1
7
lay=1
Please select:
-----------------------------
     1:  插入
     2:  删除
     3:  查找
     4:  遍历
     5:  遍历所有层
     0:  退出
-----------------------------
5
level 5:  4  
level 4:  4  
level 3:  4  
level 2:  4  
level 1:  4  7  
level 0:  1  4  7  
Please select:
----------------------------
     1:  插入
     2:  删除
     3:  查找
     4:  遍历
     5:  遍历所有层
     0:  退出
-----------------------------
1
2
lay=0
Please select:
-----------------------------
     1:  插入
     2:  删除
     3:  查找
     4:  遍历
     5:  遍历所有层
     0:  退出
-----------------------------
5
level 5:  4  
level 4:  4  
level 3:  4  
level 2:  4  
level 1:  4  7  
level 0:  1  2  4  7  
Please select:
-----------------------------
     1:  插入
     2:  删除
     3:  查找
     4:  遍历
     5:  遍历所有层
     0:  退出
-----------------------------
3
3
find fail!
Please select:
-----------------------------
     1:  插入
     2:  删除
     3:  查找
     4:  遍历
     5:  遍历所有层
     0:  退出
-----------------------------
3
2
find success!
Please select:
-----------------------------
     1:  插入
     2:  删除
     3:  查找
     4:  遍历
     5:  遍历所有层
     0:  退出
-----------------------------
2
2
2
Please select:
-----------------------------
     1:  插入
     2:  删除
     3:  查找
     4:  遍历
     5:  遍历所有层
     0:  退出
-----------------------------
5
level 5:  4  
level 4:  4  
level 3:  4  
level 2:  4  
level 1:  4  7  
level 0:  1  4  7  
Please select:
-----------------------------
     1:  插入
     2:  删除
     3:  查找
     4:  遍历
     5:  遍历所有层
     0:  退出
-----------------------------

到此这篇关于详解Java中跳跃表的原理和实现的文章就介绍到这了,更多相关Java跳跃表内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！