pytorch中backward()方法如何自动求梯度 / 张生荣

pytorch backward()方法自动求梯度

1、区分源张量和结果张量

x = torch.arange(-8.0, 8.0, 0.1, requires_grad= True)
y = x.relu()

x为源张量，基于源张量x得到的张量y为结果张量。

2、如何使用backward()方法自动求梯度

一个标量调用它的backward()方法后，会根据链式法则自动计算出源张量的梯度值。

2.1、结果张量是一维张量

基于以上例子，就是将一维张量y变成标量后，然后通过调用backward()方法，就能自动计算出x的梯度值。

那么，如何将一维张量y变成标量呢？

一般通过对一维张量y进行求和来实现，即y.sum()。

一个一维张量就是一个向量，对一维张量求和等同于这个向量点乘一个等维的单位向量，使用求和得到的标量y.sum()对源张量x求导与y的每个元素对x的每个元素求导结果是一样的，最终对源张量x的梯度求解没有影响。

因此，代码如下：

y.sum().backward() 
x.grad

2.2、结果张量是二维张量或更高维张量

撇开上面例子，结果变量y可能是二维张量或者更高维的张量，这时可以理解为一般点乘一个等维的单位张量（点乘，是向量中的概念，这样描述只是方便理解）

代码如下：

y.backward(torch.ones_like(y))#grad_tensors=torch.ones_like(y)
x.grad

pytorch中的梯度计算

什么是梯度？

在一元函数中,某点的梯度标的就说某点的导数. 在多元函数中某点的梯度表示的是由每个自变量所对应的偏导数所组成的向量

在前面的线性回归中就像y = wx + b方程中求出w参数最优的解，就需要对w参数进行偏导数的求取，然后通过偏导数的值来调整w参数以便找到最优解。

自动计算梯度和偏导数

在PyTorch中可以使用torch.autograd.backward()方法来自动计算梯度

在定义张量时，可以指定requires_grad=True表示这个张量可以求偏导数

import torch
# 随机出张量x 指定可以计算偏导数
x = torch.randn(1,requires_grad=True)
# y和z张量不可以求偏导
y = torch.randn(1)
z = torch.randn(1)
# f1中有张量允许求偏导
f1 = 2*x + y
# f2中没有张量可以允许求偏导
f2 = y + z
# 打印两个方程的梯度
print(f1.grad_fn)
print(f2.grad_fn)

得出结论：

f1中有允许可以求偏导的张量存在才可以求梯度
grad_fn为梯度

1. 求x的偏导数

# 可以求梯度的变量先使用backward()反向传播
f1.backward()
# 使用张量的grad属性拿到偏导数的值
x.grad

2. 停止梯度的计算

张量.requires_grad_(False)

# 创建张量 指定可以求偏导
a = torch.randn(2,2,requires_grad=True)
# a对应的b变量
b = ((a * 3)/(a - 1))
# 查看梯度
print(b.grad_fn)
# 停止a张量可以求偏导
a.requires_grad_(False)
# 再次指定b对应变量
b = ((a * 3) / (a - 1))
# 为None了
print(b.grad_fn)

3. 获取到可以求偏导数的张量相同的内容，但是新变量不可以求偏导

张量.detach()方法

a = torch.randn(2,2,requires_grad=True)
# 可以求偏导的张量返回一个相同的张量但是不可以求偏导数
b = a.detach()
print(a.requires_grad)
print(b.requires_grad)

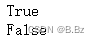
4. 在作用域中张量不可计算偏导数

with torch.no_grad(): 内的整个作用域

a = torch.randn(2, 2, requires_grad=True)
print((a ** 2).requires_grad)
with torch.no_grad():
    print((a ** 2).requires_grad)

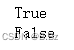
梯度的清空

在PyTorch中,如果我们利用torch.autograd.backward()方法求解张量的梯度, 在多次运行该函数的情况下, 该函数会将计算得到的梯度累加起来。

所以在函数中计算张量的偏导数，每次计算完修改完参数要清空梯度的计算。

不清空梯度计算：

x = torch.ones(4, requires_grad=True)
y = (2*x + 1).sum()
z = (2*x).sum()
y.backward()
print("第一次偏导:",x.grad)
z.backward()
print("第二次偏导:",x.grad)

会累加

使用张量.grad.zero_()方法清空梯度的计算：

x = torch.ones(4, requires_grad=True)
y = (2*x + 1).sum()
z = (2*x).sum()
y.backward()
x.grad.zero_()
print("第一次偏导:",x.grad)
z.backward()
print("第二次偏导:",x.grad)

总结

以上为个人经验，希望能给大家一个参考，也希望大家多多支持我们。

pytorch中backward()方法如何自动求梯度

目录