算法系列15天速成 第七天 线性表【上】

哈哈，我们的数据也一样，存在这三种基本关系，用术语来说就是:

<1>  线性关系。
<2>  树形关系。
<3>  网状关系。

一： 线性表

1 概念：
                 线性表也就是关系户中最简单的一种关系，一对一。
                  如：学生学号的集合就是一个线性表。

2 特征：
                 ① 有且只有一个“首元素“。
                 ② 有且只有一个“末元素”。
                 ③ 除“末元素”外，其余元素均有唯一的后继元素。
                 ④ 除“首元素”外，其余元素均有唯一的前驱元素。

3 存储划分：
                  ① 如果把线性表用“顺序存储”，那么就是“顺序表”。
                  ② 如果把线性表用“链式存储”，那么就是“链表”。

4  常用操作：添加，删除，插入，查找，遍历，统计。

今天主要就说说“线性表”的“顺序存储”。

那么下面就简单的浅析一下这个操作的原理和复杂度。
     <1> 初始化顺序表： 
                           这个操作其实还是蛮简单的，设置length=0，也就是O(1)的时间。
     <2> 求顺序表长度： 
                           这个不解释，O(1)的时间。
     <3> 添加节点：     
                           因为是顺序表，所以添加的节点直接会放到数组的末尾，时间也是O(1)的。
     <4> 插入节点：
                           这个还是有点小麻烦的，主要也就是说分两种情况：
                                    ①：当插入节点在数组的最后，那么这个“插入”其实就是”添加“操作，时间当然是O(1)。
                                    ②：当插入节点在数组的开头，那就悲催了，被插入节点的后续元素都要向后移动一位，
                                          　　也就让整个数组一阵痉挛，效率低下可想而知，时间复杂度退化为O(n)。
      <5> 删除节点：     
                             这个跟“插入”的道理是一样的，也要分两个情况，
                                     ①：当删除的元素在数组的最后，不用移位，谢天谢地，时间为O(1)。
                                     ②： 当删除的元素在数组的开头，删除节点处的元素都要统统向前移位，同样也是一阵痉挛，
                                           　   时间复杂度也退化为O(n)。
      <6> 按序号查找节点：
                               大家都知道，顺序表的存储地址是连续的，所以第N个元素地址公式为：（N-1）X 数据存储长度。
                                        哈哈，这就是顺序表得瑟的地方，查找的时间复杂度为O(1)。
      <7> 按关键字查找： 
                                 嗯，这个在日常开发中用的最多的，那么就避免不了将key的值在我们的list中查找，前期也说过，
                                        最快的查找是O(1),当然他是用空间来换取时间的，最慢的查找是O(n)，那么这里我们就一个for
                                        循环搞定，时间复杂度为O(n)。

说了这么多，目的就是预先评估算法的执行效率，给我们带来一手的参考资料，做到真正的运筹帷幄，决胜千里之外。
这也是我们学习算法的目的，到时候不会让我们说tnd，程序歇菜了，我也歇菜了。

好，现在是上代码时间。

代码如下:

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;

namespace SeqList
{
    public class Program
    {
        static void Main(string[] args)
        {
            SeqList seq = new SeqList();
            SeqListType<Student> list = new SeqListType<Student>();
            Console.WriteLine("\n********************** 添加二条数据 ************************\n");
            seq.SeqListAdd<Student>(list, new Student() { ID = "1", Name = "一线码农", Age = 23 });
            seq.SeqListAdd<Student>(list, new Student() { ID = "3", Name = "huangxincheng520", Age = 23 });
            Console.WriteLine("添加成功");
            //展示数据
            Display(list);
            Console.WriteLine("\n********************** 正在搜索Name=“一线码农”的实体 ************************\n");
            var student = seq.SeqListFindByKey<Student, string>(list, "一线码农", s => s.Name);
            Console.WriteLine("\n********************** 展示一下数据 ************************\n");
            if (student != null)
                Console.WriteLine("ID:" + student.ID + ",Name:" + student.Name + ",Age:" + student.Age);
            else
                Console.WriteLine("对不起，数据未能检索到。");
            Console.WriteLine("\n********************** 插入一条数据 ************************\n");
            seq.SeqListInsert(list, 1, new Student() { ID = "2", Name = "博客园", Age = 40 });
            Console.WriteLine("插入成功");
            //展示一下
            Display(list);
            Console.WriteLine("\n********************** 删除一条数据 ************************\n");
            seq.SeqListDelete(list, 0);
            Console.WriteLine("删除成功");
            //展示一下数据
            Display(list);
            Console.Read();
        }

///<summary>
/// 展示输出结果
///</summary>
        static void Display(SeqListType<Student> list)
        {
            Console.WriteLine("\n********************** 展示一下数据 ************************\n");
            if (list == null || list.ListLen == 0)
            {
                Console.WriteLine("呜呜，没有数据");
                return;
            }
            for (int i = 0; i < list.ListLen; i++)
            {
                Console.WriteLine("ID:" + list.ListData[i].ID + ",Name:" + list.ListData[i].Name + ",Age:" + list.ListData[i].Age);
            }
        }
    }

#region 学生的数据结构
    ///<summary>
/// 学生的数据结构
///</summary>
    public class Student
    {
        public string ID { get; set; }
        public string Name { get; set; }
        public int Age { get; set; }
    }
    #endregion

#region 定义一个顺序表的存储结构
    ///<summary>
/// 定义一个顺序表的存储结构
///</summary>
    public class SeqListType<T>
    {
        private const int maxSize = 100;
        public int MaxSize { get { return maxSize; } }
        //数据为100个存储空间
        public T[] ListData = new T[maxSize];
        public int ListLen { get; set; }
    }
    #endregion

#region 顺序表的相关操作
    ///<summary>
///顺序表的相关操作
///</summary>
    public class SeqList
    {
        #region 顺序表初始化
        ///<summary>
/// 顺序表初始化
///</summary>
///<param name="t"></param>
        public void SeqListInit<T>(SeqListType<T> t)
        {
            t.ListLen = 0;
        }
        #endregion

#region 顺序表的长度
        ///<summary>
/// 顺序表的长度
///</summary>
///<param name="t"></param>
///<returns></returns>
        public int SeqListLen<T>(SeqListType<T> t)
        {
            return t.ListLen;
        }
        #endregion

#region 顺序表的添加
        ///<summary>
///顺序表的添加
///</summary>
///<param name="t"></param>
///<returns></returns>
        public bool SeqListAdd<T>(SeqListType<T> t, T data)
        {
            //防止数组溢出
            if (t.ListLen == t.MaxSize)
                return false;
            t.ListData[t.ListLen++] = data;
            return true;
        }
        #endregion

#region 顺序表的插入操作
        ///<summary>
/// 顺序表的插入操作
///</summary>
///<param name="t"></param>
///<param name="n"></param>
///<param name="data"></param>
///<returns></returns>
        public bool SeqListInsert<T>(SeqListType<T> t, int n, T data)
        {
            //首先判断n是否合法
            if (n < 0 || n > t.MaxSize - 1)
                return false;
            //说明数组已满，不能进行插入操作
            if (t.ListLen == t.MaxSize)
                return false;
            //需要将插入点的数组数字依次向后移动
            for (int i = t.ListLen - 1; i >= n; i--)
            {
                t.ListData[i + 1] = t.ListData[i];
            }

//最后将data插入到腾出来的位置
            t.ListData[n] = data;
            t.ListLen++;
            return true;
        }
        #endregion

#region 顺序表的删除操作
        ///<summary>
/// 顺序表的删除操作
///</summary>
///<param name="t"></param>
///<param name="n"></param>
///<returns></returns>
        public bool SeqListDelete<T>(SeqListType<T> t, int n)
        {
            //判断删除位置是否非法
            if (n < 0 || n > t.ListLen - 1)
                return false;
            //判断数组是否已满
            if (t.ListLen == t.MaxSize)
                return false;
            //将n处后的元素向前移位
            for (int i = n; i < t.ListLen; i++)
                t.ListData[i] = t.ListData[i + 1];
            //去掉数组最后一个元素
            --t.ListLen;
            return true;
        }
        #endregion

#region 顺序表的按序号查找
        ///<summary>
/// 顺序表的按序号查找
///</summary>
///<param name="t"></param>
///<param name="n"></param>
///<returns></returns>
        public T SeqListFindByNum<T>(SeqListType<T> t, int n)
        {
            if (n < 0 || n > t.ListLen - 1)
                return default(T);
            return t.ListData[n];
        }
        #endregion

#region  顺序表的关键字查找
        ///<summary>
/// 顺序表的关键字查找
///</summary>
///<typeparam name="T"></typeparam>
///<typeparam name="W"></typeparam>
///<param name="t"></param>
///<param name="key"></param>
///<param name="where"></param>
///<returns></returns>
        public T SeqListFindByKey<T, W>(SeqListType<T> t, string key, Func<T, W> where) where W : IComparable
        {

for (int i = 0; i < t.ListLen; i++)
            {
                if (where(t.ListData[i]).CompareTo(key) == 0)
                {
                    return t.ListData[i];
                }
            }
            return default(T);
        }
        #endregion
    }
    #endregion
}

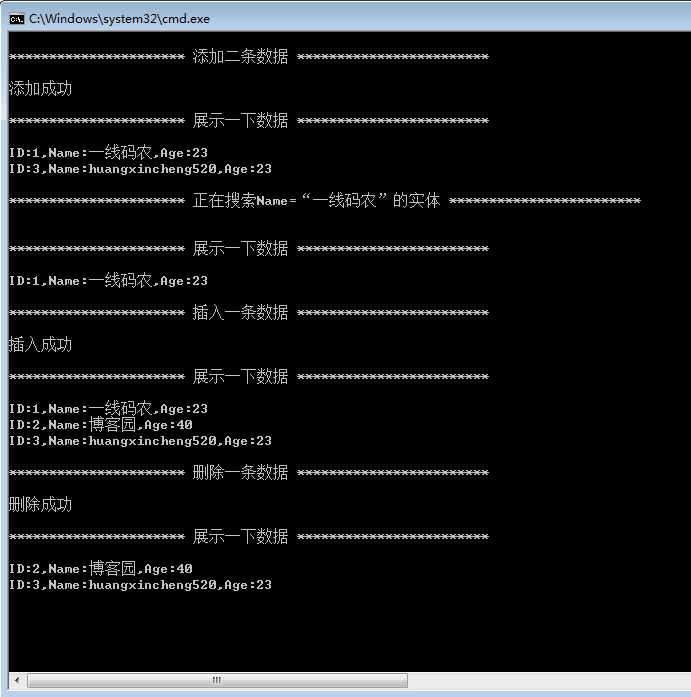
运行结果：