Java动态规划方式解决不同的二叉搜索树

目录
  • 一、题目描述
  • 二、思路
  • 三、代码

一、题目描述

给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

来源：https://leetcode.cn/problems/unique-binary-search-trees/

二、思路

本题可以使用动态规划的方式解决，我们先来看一下大题思路。以 n = 3 为例，n = 3 时的不同的二叉搜索树数目，可以通过分别 以 1 为根节点，以 2 为根节点，以 3 为根节点 的不同的二叉搜索树的数量加和获得。

那么问题就来到了如何得到 以 1 为根节点，以 2 为根节点，以 3 为根节点 的不同二叉搜索树数量。这就是我们动态规划，主要处理的问题。

  • 以 1 为根节点 时： 此时其左子树具有 dp[1-1] 种选择（左子树无节点），右子树具有 dp[3-1] 种选择（节点 2，3）
  • 以 2 为根节点 时： 此时其左子树具有 dp[2-1] 种选择（节点 1），右子树具有 dp[3-2] 种选择（节点 3）
  • 以 3 为根节点时： 此时其左子树具有 dp[3-1] 种选择（节点 1，2），右子树具有 dp[3-3] 中选择（右子树无节点）

因此 最终结果为

dp[1-1] * dp[3-1] + dp[2-1] * dp[3-2] + dp[3-1] * dp[3-3]

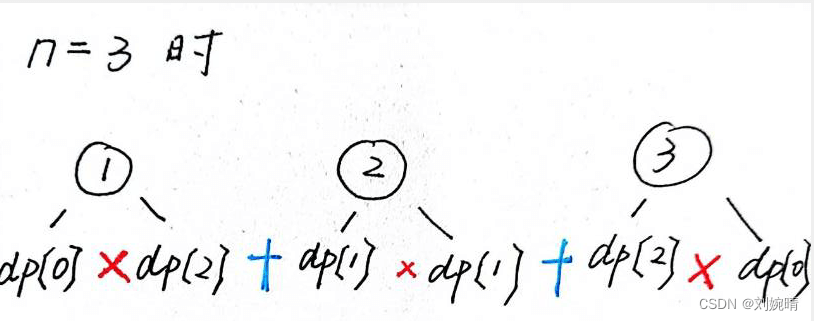
分析完了 n = 3 的情况，下面我们来看一下一般情况：

1. dp数组以及下标的含义:

dp[] 数组表示二叉搜索树数量，下标 i 表示当 n = i 时，所含的二叉搜索树数量

2. 确定递推公式:

dp[i] += dp[i-1] * dp[i-j] (其中 1<=j<=i, 表示以 j 为根节点的二叉搜索树)

3. dp数组如何初始化

  • 当二叉树一个节点都没有，即 dp[0] 时 ，二叉搜索树只有一种情况 dp[0] = 1
  • 当二叉树只有一个节点时，即 dp[1] 时，二叉搜索树只有一种情况 dp[1] = 1

4. 确定遍历顺序:

节点数为 3 的二叉搜索树种类数，需要用节点数为 2 的二叉搜索树推出，因此顺序遍历 从 3 ~ n 即可

三、代码

    // 不同的二叉搜索树
    public int numTrees(int n) {
        int[] dp = new int[n+1];
        dp[0] = 1;
        dp[1] = 1; // 初始化动态规划数组
        for(int i=2; i<n+1; i++){
            for(int j=1; j<=i; j++){ // 分别以 1 ~ i 为根节点，计算二叉树种类数，累加到结果中
                dp[i] += dp[j-1]*dp[i-j];
            }
        }
        return dp[n];
    }

到此这篇关于Java动态规划方式解决不同的二叉搜索树的文章就介绍到这了,更多相关Java二叉搜索树内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！

赞 (0)

相关推荐

  • Java通过动态规划设计股票买卖最佳时机

    Java通过动态规划设计股票买卖最佳时机

    目录 买卖股票的最佳时机 动态规划 买卖股票的最佳时机 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格.你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票.设计一个算法来计算你所能获取的最大利润.返回你可以从这笔交易中获取的最大利润.如果你不能获取任何利润,返回 0 . 示例: 链接:https://leetcode.cn/problems/best-time-to-buy-and-sell-stock 动态规划

  • Java动态规划之丑数问题实例讲解

    Java动态规划之丑数问题实例讲解

    问题描述: 我们把只包含质因子 2.3 和 5 的数称作丑数(Ugly Number).求按从小到大的顺序的第 n 个丑数. 注: 1也是丑数 思路: 我们来分析一下丑数如何得到,肯定是由前面的丑数乘2,乘3或者乘5得到,因此这是一道动态规划题. 使用 dp[i] 记录第i个丑数, 初始值dp[0] = 1,返回 dp[n-1] 使用 a,b,c 记录以及 2,3,5 分别乘到了第几个丑数 动态规划方程为: dp[i] = Math.min(Math.min(dp[a]*2, dp[b]*3),

  • Java数据结构超详细分析二叉搜索树

    Java数据结构超详细分析二叉搜索树

    目录 1.搜索树的概念 2.二叉搜索树的简单实现 2.1查找 2.2插入 2.3删除 2.4修改 3.二叉搜索树的性能 1.搜索树的概念 二叉搜索树是一种特殊的二叉树,又称二叉查找树,二叉排序树,它有几个特点: 如果左子树存在,则左子树每个结点的值均小于根结点的值. 如果右子树存在,则右子树每个结点的值均大于根结点的值. 中序遍历二叉搜索树,得到的序列是依次递增的. 二叉搜索树的左右子树均为二叉搜索树. 二叉搜索树的结点的值不能发生重复. 2.二叉搜索树的简单实现 我们来简单实现以下搜索树,就不

  • 在Java中实现二叉搜索树的全过程记录

    在Java中实现二叉搜索树的全过程记录

    目录 二叉搜索树 有序符号表的 API 实现二叉搜索树 二叉搜索树类 查找 插入 最小/大的键 小于等于 key 的最大键/大于等于 key 的最小键 根据排名获得键 根据键获取排名 删除 总结 二叉搜索树 二叉搜索树结合了无序链表插入便捷和有序数组二分查找快速的特点,较为高效地实现了有序符号表.下图显示了二叉搜索树的结构特点(图片来自<算法第四版>): 可以看到每个父节点下都可以连着两个子节点,键写在节点上,其中左边的子节点的键小于父节点的键,右节点的键大于父节点的键.每个父节点及其后代节点

  • Java使用动态规划算法思想解决背包问题

    Java使用动态规划算法思想解决背包问题

    目录 动态规划算法 动态规划算法的思想 最优性原理 动态规划算法的三大特点 动态规划算法中的0/1背包问题 动态规划算法的优点 小结 动态规划算法 动态规划算法的思想 动态规划算法处理的对象是多阶段复杂决策问题,动态规划算法和分治算法类似,其基本思想也是将待求解问题分解成若干个子问题(阶段),然后分别求解各个子问题(阶段),最后将子问题的解组合起来得到原问题的解,但是与分治算法不同的是,子问题往往不是相互独立的,而是相互联系又相互区别的 动态规划算法问题求解的目标是获取导致问题最优解的最优决策序

  • Java数据结构之二叉搜索树详解

    Java数据结构之二叉搜索树详解

    目录 前言 性质 实现 节点结构 初始化 插入节点 查找节点 删除节点 最后 前言 今天leetcode的每日一题450是关于删除二叉搜索树节点的,题目要求删除指定值的节点,并且需要保证二叉搜索树性质不变,做完之后,我觉得这道题将二叉搜索树特性凸显的很好,首先需要查找指定节点,然后删除节点并且保持二叉搜索树性质不变,就想利用这个题目讲讲二叉搜索树. 二叉搜索树作为一个经典的数据结构,具有链表的快速插入与删除的特点,同时查询效率也很优秀,所以应用十分广泛,例如在文件系统和数据库系统一般会采用这种数

  • Java动态规划之硬币找零问题实现示例

    目录 问题描述: 问题分析: 具体的过程如下: 动态规划(dynamic programming)是运筹学的一个分支,是求解决策过程(decision process)最优化的数学方法.20世纪50年代初美国数学家R.E.Bellman等人在研究多阶段决策过程(multistep decision process)的优化问题时,提出了著名的最优化原理(principle of optimality),把多阶段过程转化为一系列单阶段问题,利用各阶段之间的关系,逐个求解,创立了解决这类过程优化问题的

  • Java动态规划方式解决不同的二叉搜索树

    Java动态规划方式解决不同的二叉搜索树

    目录 一.题目描述 二.思路 三.代码 一.题目描述 给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数. 来源:https://leetcode.cn/problems/unique-binary-search-trees/ 二.思路 本题可以使用动态规划的方式解决,我们先来看一下大题思路.以 n = 3 为例,n = 3 时的不同的二叉搜索树数目,可以通过分别 以 1 为根节点,以 2 为根节点,以 3 为根节点

  • Java 求解如何把二叉搜索树转换为累加树

    Java 求解如何把二叉搜索树转换为累加树

    一.题目 给出二叉搜索树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和. 提醒一下,二叉搜索树满足下列约束条件: 节点的左子树仅包含键 小于 节点键的节点. 节点的右子树仅包含键 大于 节点键的节点. 左右子树也必须是二叉搜索树. 二.题解 观察示例图发现,树的遍历顺序为右,中,左的顺序,每个节点的值,是按照这个顺序累加的状态 由于是需要累加,所以需要pre指针记录当前遍历节点

  • Java C++ 算法题解leetcode669修剪二叉搜索树示例

    Java C++ 算法题解leetcode669修剪二叉搜索树示例

    目录 题目要求 思路一:模拟迭代 Java C++ 思路二:递归 Java C++ Rust 题目要求 思路一:模拟迭代 依次判断每个节点是否合法: 首先找出结果的根,若原根小了就拉右边的过来,大了拉左边的过来做新根: 然后分别判断左右子树的大小,由于二叉搜索树的性质,子树只需要判断一边就好: 左子树判断是否>low,合法就向左下走,不合法往右下: 右子树判断是否<high,合法就向右下走,不合法往左下. Java class Solution { public TreeNode trimBS

  • C语言实现二叉搜索树的完整总结

    C语言实现二叉搜索树的完整总结

    1. 二叉树的构建 我们都知道二叉搜索树的特点是:当前节点的值大于它的左子树的值,小于等于右子树的值.所以我们这里可以通过迭代的方式构建二叉搜索树,当然也可以通过递归的方式构建二叉树. 定义一个结构体,表示节点: typedef struct NODE{ int va; struct NODE *left,*right; }Node; ①通过迭代的方式实现二叉搜索树的构建,值得注意的是,这种方式构建二叉搜索树的时候,需要定义一个变量,表示这个节点插入的位置是父节点的左子节点还是右子节点的位置,同

  • Java创建二叉搜索树,实现搜索,插入,删除的操作实例

    Java实现的二叉搜索树,并实现对该树的搜索,插入,删除操作(合并删除,复制删除) 首先我们要有一个编码的思路,大致如下: 1.查找:根据二叉搜索树的数据特点,我们可以根据节点的值得比较来实现查找,查找值大于当前节点时向右走,反之向左走! 2.插入:我们应该知道,插入的全部都是叶子节点,所以我们就需要找到要进行插入的叶子节点的位置,插入的思路与查找的思路一致. 3.删除: 1)合并删除:一般来说会遇到以下几种情况,被删节点有左子树没右子树,此时要让当前节点的父节点指向当前节点的左子树:当被删节点

  • Java二叉搜索树基础原理与实现方法详解

    本文实例讲述了Java二叉搜索树基础原理与实现方法.分享给大家供大家参考,具体如下: 前言:本文通过先通过了解一些二叉树基础知识,然后在转向学习二分搜索树. 1 树 1.1 树的定义 树(Tree)是n(n>=0)个节点的有限集.n=0时称为空树.在任意一颗非空树中: (1)有且仅有一个特定的称为根(Root)的节点: (2)当n>1时,其余节点可分为m(m>0)个互不相交的有限集T1.T2........Tn,其中每一个集合本身又是一棵树,并且称为根的子树. 此外,树的定义还需要强调以

  • Java基础之二叉搜索树的基本操作

    Java基础之二叉搜索树的基本操作

    一.二叉搜索树插入元素 /** * user:ypc: * date:2021-05-18; * time: 15:09; */ class Node { int val; Node left; Node right; Node(int val) { this.val = val; } } public void insert(int key) { Node node = new Node(key); if (this.root == null) { root = node; } Node cu

  • Java实现二叉搜索树的插入、删除功能

    Java实现二叉搜索树的插入、删除功能

    二叉树的结构 public class TreeNode { int val; TreeNode left; TreeNode right; TreeNode() { } TreeNode(int val) { this.val = val; } } 中序遍历 中序遍历:从根节点开始遍历,遍历顺序是:左子树->当前节点->右子树,在中序遍历中,对每个节点来说: 只有当它的左子树都被遍历过了(或者没有左子树),它才会被遍历到.在遍历右子树之前,一定会先遍历当前节点. 中序遍历得到的第一个节点是没

  • Java 实现二叉搜索树的查找、插入、删除、遍历

    Java 实现二叉搜索树的查找、插入、删除、遍历

    由于最近想要阅读下JDK1.8 中HashMap的具体实现,但是由于HashMap的实现中用到了红黑树,所以我觉得有必要先复习下红黑树的相关知识,所以写下这篇随笔备忘,有不对的地方请指出- 学习红黑树,我觉得有必要从二叉搜索树开始学起,本篇随笔就主要介绍Java实现二叉搜索树的查找.插入.删除.遍历等内容. 二叉搜索树需满足以下四个条件: 若任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值: 若任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值: 任意节点的左.右子

随机推荐