PyTorch: 梯度下降及反向传播的实例详解

线性模型

线性模型介绍

线性模型是很常见的机器学习模型，通常通过线性的公式来拟合训练数据集。训练集包括(x,y)，x为特征,y为目标。如下图：

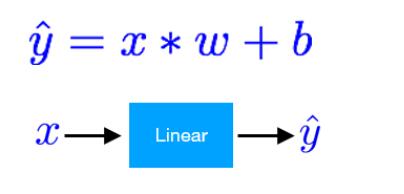
将真实值和预测值用于构建损失函数，训练的目标是最小化这个函数，从而更新w。当损失函数达到最小时(理想上,实际情况可能会陷入局部最优)，此时的模型为最优模型，线性模型常见的的损失函数：

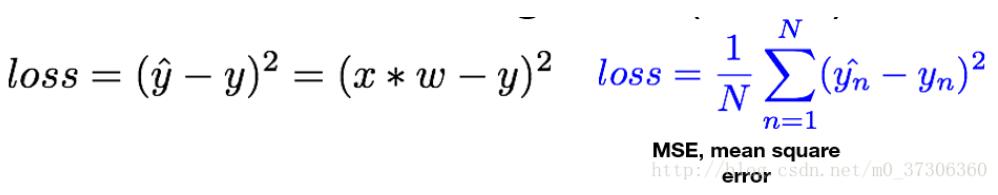
线性模型例子

下面通过一个例子可以观察不同权重(w)对模型损失函数的影响。

#author:yuquanle
#data:2018.2.5
#Study of Linear Model
import numpy as np
import matplotlib.pyplot as plt

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

def forward(x):
  return x * w

def loss(x, y):
  y_pred = forward(x)
  return (y_pred - y)*(y_pred - y)

w_list = []
mse_list = []

for w in np.arange(0.0, 4.1, 0.1):
  print("w=", w)
  l_sum = 0
  for x_val, y_val in zip(x_data, y_data):
    # error
    l = loss(x_val, y_val)
    l_sum += l
  print("MSE=", l_sum/3)
  w_list.append(w)
  mse_list.append(l_sum/3)

plt.plot(w_list, mse_list)
plt.ylabel("Loss")
plt.xlabel("w")
plt.show()

输出结果：
w= 0.0
MSE= 18.6666666667
w= 0.1
MSE= 16.8466666667
w= 0.2
MSE= 15.12
w= 0.3
MSE= 13.4866666667
w= 0.4
MSE= 11.9466666667
w= 0.5
MSE= 10.5
w= 0.6
MSE= 9.14666666667

调整w，loss变化图：

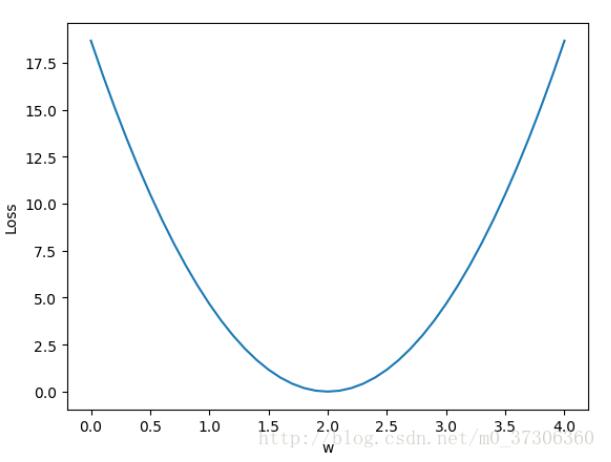
可以发现当w=2时，loss最小。但是现实中最常见的情况是，我们知道数据集，定义好损失函数之后(loss)，我们并不会从0到n去设置w的值，然后求loss，最后选取使得loss最小的w作为最佳模型的参数。更常见的做法是，首先随机初始化w的值，然后根据loss函数定义对w求梯度，然后通过w的梯度来更新w的值，这就是经典的梯度下降法思想。

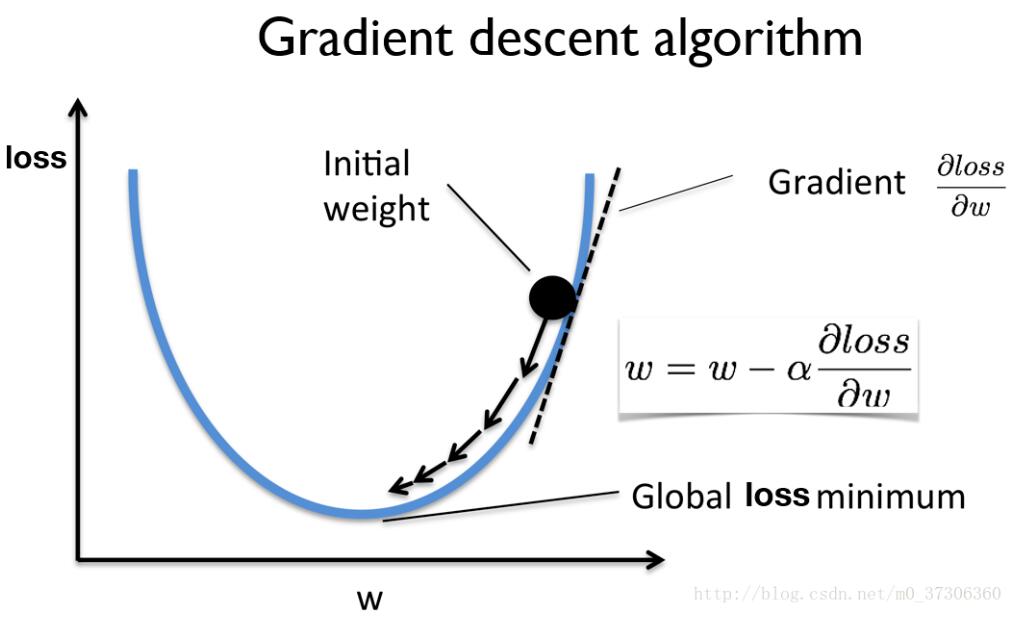
梯度下降法

梯度的本意是一个向量，表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。

梯度下降是迭代法的一种,可以用于求解最小二乘问题(线性和非线性都可以)。在求解机器学习算法的模型参数，即无约束优化问题时，梯度下降（Gradient Descent）是最常采用的方法之一，另一种常用的方法是最小二乘法。在求解损失函数的最小值时，可以通过梯度下降法来一步步的迭代求解，得到最小化的损失函数和模型参数值。即每次更新参数w减去其梯度(通常会乘以学习率)。

#author:yuquanle
#data:2018.2.5
#Study of SGD

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

# any random value
w = 1.0

# forward pass
def forward(x):
  return x * w

def loss(x, y):
  y_pred = forward(x)
  return (y_pred - y)*(y_pred - y)

# compute gradient (loss对w求导)
def gradient(x, y):
  return 2*x*(x*w - y)

# Before training
print("predict (before training)", 4, forward(4))

# Training loop
for epoch in range(20):
  for x, y in zip(x_data, y_data):
    grad = gradient(x, y)
    w = w - 0.01 * grad
    print("\t grad: ",x, y, grad)
    l = loss(x, y)
  print("progress:", epoch, l)

# After training
print("predict (after training)", 4, forward(4))

输出结果：
predict (before training) 4 4.0
   grad: 1.0 2.0 -2.0
   grad: 2.0 4.0 -7.84
   grad: 3.0 6.0 -16.2288
progress: 0 4.919240100095999
   grad: 1.0 2.0 -1.478624
   grad: 2.0 4.0 -5.796206079999999
   grad: 3.0 6.0 -11.998146585599997
progress: 1 2.688769240265834
   grad: 1.0 2.0 -1.093164466688
   grad: 2.0 4.0 -4.285204709416961
   grad: 3.0 6.0 -8.87037374849311
progress: 2 1.4696334962911515
   grad: 1.0 2.0 -0.8081896081960389
   grad: 2.0 4.0 -3.1681032641284723
   grad: 3.0 6.0 -6.557973756745939
progress: 3 0.8032755585999681
   grad: 1.0 2.0 -0.59750427561463
   grad: 2.0 4.0 -2.3422167604093502
   grad: 3.0 6.0 -4.848388694047353
progress: 4 0.43905614881022015
   grad: 1.0 2.0 -0.44174208101320334
   grad: 2.0 4.0 -1.7316289575717576
   grad: 3.0 6.0 -3.584471942173538
progress: 5 0.2399802903801062
   grad: 1.0 2.0 -0.3265852213980338
   grad: 2.0 4.0 -1.2802140678802925
   grad: 3.0 6.0 -2.650043120512205
progress: 6 0.1311689630744999
   grad: 1.0 2.0 -0.241448373202223
   grad: 2.0 4.0 -0.946477622952715
   grad: 3.0 6.0 -1.9592086795121197
progress: 7 0.07169462478267678
   grad: 1.0 2.0 -0.17850567968888198
   grad: 2.0 4.0 -0.6997422643804168
   grad: 3.0 6.0 -1.4484664872674653
progress: 8 0.03918700813247573
   grad: 1.0 2.0 -0.13197139106214673
   grad: 2.0 4.0 -0.5173278529636143
   grad: 3.0 6.0 -1.0708686556346834
progress: 9 0.021418922423117836
predict (after training) 4 7.804863933862125

反向传播

但是在定义好模型之后，使用pytorch框架不需要我们手动的求导，我们可以通过反向传播将梯度往回传播。通常有二个过程，forward和backward:

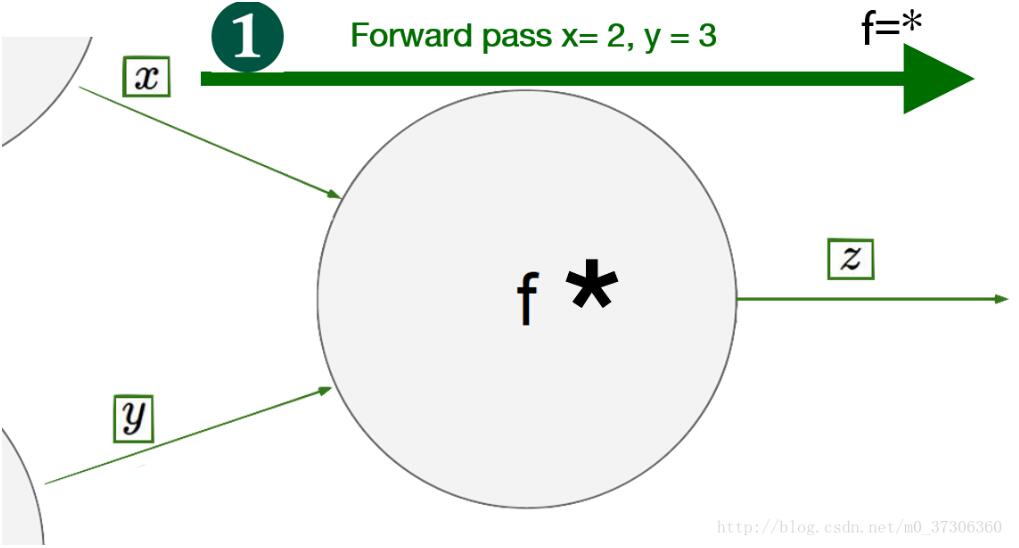
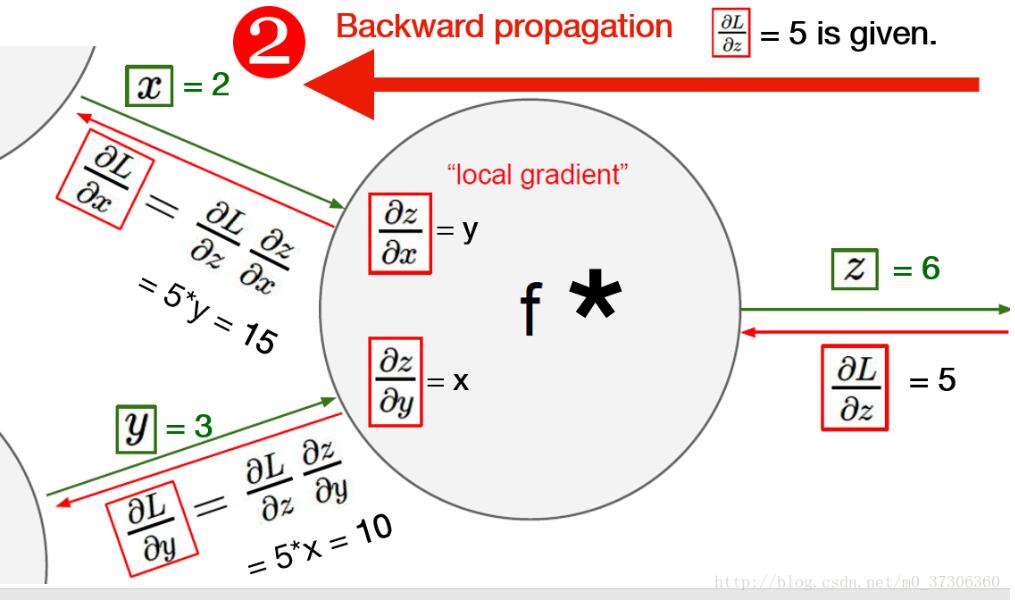
#author:yuquanle
#data:2018.2.6
#Study of BackPagation

import torch
from torch import nn
from torch.autograd import Variable

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

# Any random value
w = Variable(torch.Tensor([1.0]), requires_grad=True)

# forward pass
def forward(x):
  return x*w

# Before training
print("predict (before training)", 4, forward(4))

def loss(x, y):
  y_pred = forward(x)
  return (y_pred-y)*(y_pred-y)

# Training: forward, backward and update weight
# Training loop
for epoch in range(10):
  for x, y in zip(x_data, y_data):
    l = loss(x, y)
    l.backward()
    print("\t grad:", x, y, w.grad.data[0])
    w.data = w.data - 0.01 * w.grad.data
    # Manually zero the gradients after running the backward pass and update w
    w.grad.data.zero_()
  print("progress:", epoch, l.data[0])

# After training
print("predict (after training)", 4, forward(4))

输出结果：
predict (before training) 4 Variable containing:
 4
[torch.FloatTensor of size 1]
   grad: 1.0 2.0 -2.0
   grad: 2.0 4.0 -7.840000152587891
   grad: 3.0 6.0 -16.228801727294922
progress: 0 7.315943717956543
   grad: 1.0 2.0 -1.478623867034912
   grad: 2.0 4.0 -5.796205520629883
   grad: 3.0 6.0 -11.998146057128906
progress: 1 3.9987640380859375
   grad: 1.0 2.0 -1.0931644439697266
   grad: 2.0 4.0 -4.285204887390137
   grad: 3.0 6.0 -8.870372772216797
progress: 2 2.1856532096862793
   grad: 1.0 2.0 -0.8081896305084229
   grad: 2.0 4.0 -3.1681032180786133
   grad: 3.0 6.0 -6.557973861694336
progress: 3 1.1946394443511963
   grad: 1.0 2.0 -0.5975041389465332
   grad: 2.0 4.0 -2.3422164916992188
   grad: 3.0 6.0 -4.848389625549316
progress: 4 0.6529689431190491
   grad: 1.0 2.0 -0.4417421817779541
   grad: 2.0 4.0 -1.7316293716430664
   grad: 3.0 6.0 -3.58447265625
progress: 5 0.35690122842788696
   grad: 1.0 2.0 -0.3265852928161621
   grad: 2.0 4.0 -1.2802143096923828
   grad: 3.0 6.0 -2.650045394897461
progress: 6 0.195076122879982
   grad: 1.0 2.0 -0.24144840240478516
   grad: 2.0 4.0 -0.9464778900146484
   grad: 3.0 6.0 -1.9592113494873047
progress: 7 0.10662525147199631
   grad: 1.0 2.0 -0.17850565910339355
   grad: 2.0 4.0 -0.699742317199707
   grad: 3.0 6.0 -1.4484672546386719
progress: 8 0.0582793727517128
   grad: 1.0 2.0 -0.1319713592529297
   grad: 2.0 4.0 -0.5173273086547852
   grad: 3.0 6.0 -1.070866584777832
progress: 9 0.03185431286692619
predict (after training) 4 Variable containing:
 7.8049
[torch.FloatTensor of size 1]
Process finished with exit code 0

以上这篇PyTorch: 梯度下降及反向传播的实例详解就是小编分享给大家的全部内容了，希望能给大家一个参考，也希望大家多多支持我们。