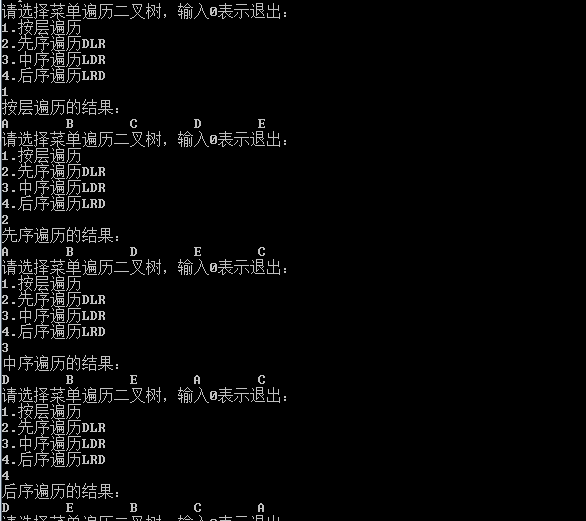
C++二叉树结构的建立与基本操作

准备数据
定义二叉树结构操作中需要用到的变量及数据等。


代码如下:

#define MAXLEN 20    //最大长度
typedef char DATA;    //定义元素类型
struct  CBTType                   //定义二叉树结点类型
{
 DATA data;           //元素数据
 CBTType * left;    //左子树结点指针
 CBTType * right;   //右子树结点指针
};

定义二叉树结构数据元素的类型DATA以及二叉树结构的数据结构CBTType。结点的具体数据保存在一个姐都DATA中，而指针left用来指向左子树结点，指针right用来指向右子树结点

初始化二叉树
初始化二叉树，将一个结点设置为二叉树的根结点。


代码如下:

CBTType * InitTree()
{
 CBTType * node;
 if(node = new CBTType)  //申请内存
 {
  cout<<"请先输入一个根节点数据："<<endl;
  cin>>node->data;
  node->left=NULL;
  node->right=NULL;
  if(node!=NULL)   //如果二叉树结点不为空
  {
   return node;  
  } else
  {
   return NULL;
  }
 }
 return NULL;
}

首先申请一个结点，然后用户输入根结点 的数据，并将左子树和右子树的指针置为空，即可完成二叉树的初始化工作。

查找结点

查找结点就是遍历二叉树中的每一个节点，逐个比较数据，当找到目标数据时将返回该数据所在结点的指针。


代码如下:

CBTType *TreeFindNode(CBTType *treeNode,DATA data)
{
 CBTType *ptr;
 if(treeNode==NULL)
 {
  return NULL;
 }else
 {
  if(treeNode->data==data)
  {
   return treeNode;
  }
  else        //分别向左右子树查找   
  {
   if(ptr=TreeFindNode(treeNode->left,data))  //左子树递归查找
   {
    return ptr;
   }
   else if(ptr=TreeFindNode(treeNode->right,data))         //右子树递归查找
   {
    return ptr;
   }
   else
   {
    return NULL;
   }
  }
 }
}

输入参数treeNode为待查找的二叉树的根结点，输入参数data为待查找的结点数据。程序中首先判断根结点是否为空，然后根据数据判断是否为根结点，然后分别向左右子树进行查找，采用递归的方法进行查找，查找到该结点则返回结点对应的指针；如果全都查找不到，则返回NULL。

添加结点
添加结点就是在二叉树中添加结点数据，添加结点时除了要输入结点数据外，还需要指定其父结点，以及添加的结点作为左子树还是右子树。然后将该结点置为其父结点的左子树或者右子树。


代码如下:

void AddTreeNode(CBTType *treeNode)
{
 CBTType *pnode,*parent;
 DATA data;
 char menusel;
 if(pnode=new CBTType)     //分配内存
 {
  cout<<"输入二叉树结点数据："<<endl;
  cin>>pnode->data;
  pnode->left=NULL;     //设置左子树为空
  pnode->right=NULL;     //设置左子树为空
  cout<<"输入该结点的父结点数据"<<endl;
  cin>>data;
  parent=TreeFindNode(treeNode,data);//查找父结点，获得结点指针
  if(!parent)
  {
   cout<<"没有找到父结点"<<endl;
   delete pnode;
   return ;
  }
  cout<<"1.添加该结点到左子树；2.添加该结点到右子树。请输入操作对应的数字。"<<endl;
  do
  {
   cin>>menusel;
   if(menusel=='1'||menusel=='2')
   {
    switch(menusel)
    {
     case '1':     //添加结点到左子树
      if(parent->left)                 //左子树不为空
      {
       cout<<"左子树结点不为空"<<endl;
      }
      else
      {
       parent->left=pnode;
       cout<<"数据添加成功！"<<endl;
      }
      break;
     case '2':     //添加结点到右子树
      if(parent->right)                 //右子树不为空
      {
       cout<<"右子树结点不为空"<<endl;
      }
      else
      {
       parent->right=pnode;
       cout<<"数据添加成功！"<<endl;
      }
      break;
     default:
      cout<<"子节点选择error!"<<endl;
      break;
    }
   }
  }while(menusel!='1'&&menusel!='2');
 }
}

输入参数treeNode为二叉树的根结点，传入根节点是为了方便查找父结点。程序中首先申请内存，然后由用户输入二叉树结点数据，并设置左右子树为空。接着指定其父结点，将其置为左子树或者右子树。

计算二叉树的深度
计算二叉树深度就是计算二叉树中结点的最大层数，这里往往需要采用递归算法来实现。


代码如下:

int TreeDepth(CBTType *treeNode)
{
 int depleft,depright;
 if(treeNode==NULL)
 {
  return 0;     //结点为空的时候，深度为0
 }
 else
 {
  depleft=TreeDepth(treeNode->left);  //左子树深度（递归调用）
  depright=TreeDepth(treeNode->right);         //右子树深度（递归调用）
  if(depleft)
  {
   return ++depleft;
  }
  else
  {
   return ++depright;
  }
 }
}

输入参数treeNode为待计算的二叉树的根结点。首先判断根节点是否为空，然后分别按照递归调用来计算左子树深度和右子树深度，从而完成整个二叉树深度的计算。

显示结点数据


代码如下:

void ShowNodeData(CBTType *treeNode)
{
 cout<<treeNode->data<<"\t";     //直接输出结点数据
}

输入参数为需要显示的结点的指针。

清空二叉树
清空二叉树就是将二叉树变成一个空树，这里也需要使用递归算法来实现。


代码如下:

void ClearTree(CBTType *treeNode)
{
 if(treeNode)        //判断当前树不为空
 {
  ClearTree(treeNode->left);            //清空左子树
  ClearTree(treeNode->right);            //清空右子树
  delete treeNode;      //释放当前结点所占用的内存 
 }
}

输入参数treeNode为待清空的二叉树的根节点。程序中按照递归的方法清空左子树和右子树以及根节点，释放结点占用的内存空间，从而完成清空操作。

遍历二叉树
遍历二叉树就是逐个查找二叉树中所有的结点，这里为了直观的显示查找的结果，将会按照查找的顺序，依次输出对应的结点 。

按层遍历算法
按层遍历算法是最直观的算法。即：首先输出第一层即根结点，然后输出第一个结点的左右子数，也就是第二层……这样循环处理，就可以逐层遍历，一层一层按照从上到下，从左到右的顺序输出结点。


代码如下:

void LevelTree(CBTType *treeNode)
{
 CBTType *p;
 CBTType *q[MAXLEN];       //定义一个队列
 int head=0,tail=0;
 if(treeNode)        //如果队首指针不为空
 {
  tail=(tail+1)%MAXLEN;             //计算循环队列队尾序号
  q[tail]=treeNode;      //二叉树根指针进入队列
  while(head!=tail)
  {
   head=(head+1)%MAXLEN;            //计算循环队列的队首序号
   p=q[head];      //获取队首元素
   ShowNodeData(p);     //输出队首元素
   if(p->left!=NULL)     //如果存在左子树
   {
    tail=(tail+1)%MAXLEN;           //计算队列的队尾序号
    q[tail]=p->left;    //左子树入队
   }
   if(p->right!=NULL)     //如果存在右子树
   {
    tail=(tail+1)%MAXLEN;           //计算队列的队尾序号
    q[tail]=p->right;    //右子树入队
   }
  }
 }
}

输入参数treeNode为需要遍历的二叉树的根结点，程序在整个处理过程中，首先从根节点开始，将每层的结点逐步进入循环队列，并且每次循环都是输出队首的一个结点数据，然后再使它的左右子树进入队列。如此循环直到队列中的所有的数据都输出完毕。

先序遍历算法
先序遍历算法就是先访问根节点，然后访问左子树，然后访问右子树。程序中可以按照递归的思想遍历左子树和右子树。


代码如下:

void DLRTree(CBTType *treeNode)
{
 if(treeNode)
 {
  ShowNodeData(treeNode);     //显示结点内容
  DLRTree(treeNode->left);    //显示左子树内容
  DLRTree(treeNode->right);    //显示右子树内容
 }
}

中序遍历算法
先序遍历算法就是先访问左子树，然后访问根节点，然后访问右子树。程序中可以按照递归的思想遍历左子树和右子树。


代码如下:

void LDRTree(CBTType *treeNode)
{
 if(treeNode)
 {

LDRTree(treeNode->left);    //显示左子树内容   
  ShowNodeData(treeNode);     //显示结点内容
  DLRTree(treeNode->right);    //显示右子树内容    
 } 
}

后序遍历算法
先序遍历算法就是先访问左子树，然后访问右子树，然后访问根节点。程序中可以按照递归的思想遍历左子树和右子树。


代码如下:

void LRDTree(CBTType *treeNode)
{
 if(treeNode)
 {
  LRDTree(treeNode->left);    //显示左子树内容 
  DLRTree(treeNode->right);    //显示右子树内容    
  ShowNodeData(treeNode);     //显示结点内容
 } 
}

完整代码示例操作：

在文件中加入头文件，然后包含上述所有函数，然后再写一个main函数即可：


代码如下:

#include<iostream>
using namespace std;
#define MAXLEN 20            //最大长度
typedef char DATA;            //定义元素类型
struct  CBTType                           /定义二叉树结点类型
{
 DATA data;     //元素数据
 CBTType * left;     //左子树结点指针
 CBTType * right;    //右子树结点指针
};
/*********************初始化二叉树***********************/
CBTType * InitTree()
{
 CBTType * node;
 if(node = new CBTType)                   //申请内存
 {
  cout<<"请先输入一个根节点数据："<<endl;
  cin>>node->data;
  node->left=NULL;
  node->right=NULL;
  if(node!=NULL)            //如果二叉树结点不为空
  {
   return node;  
  } else
  {
   return NULL;
  }
 }
 return NULL;
}
/***********************查找结点*************************/
CBTType *TreeFindNode(CBTType *treeNode,DATA data)
{
 CBTType *ptr;
 if(treeNode==NULL)
 {
  return NULL;
 }else
 {
  if(treeNode->data==data)
  {
   return treeNode;
  }
  else        //分别向左右子树查找   
  {
   if(ptr=TreeFindNode(treeNode->left,data))  //左子树递归查找
   {
    return ptr;
   }
   else if(ptr=TreeFindNode(treeNode->right,data))         //右子树递归查找
   {
    return ptr;
   }
   else
   {
    return NULL;
   }
  }
 }
}
/**********************添加结点*************************/
void AddTreeNode(CBTType *treeNode)
{
 CBTType *pnode,*parent;
 DATA data;
 char menusel;
 if(pnode=new CBTType)              //分配内存
 {
  cout<<"输入二叉树结点数据："<<endl;
  cin>>pnode->data;
  pnode->left=NULL;     //设置左子树为空
  pnode->right=NULL;     //设置左子树为空
  cout<<"输入该结点的父结点数据"<<endl;
  cin>>data;
  parent=TreeFindNode(treeNode,data);                     //查找父结点，获得结点指针
  if(!parent)
  {
   cout<<"没有找到父结点"<<endl;
   delete pnode;
   return ;
  }
  cout<<"1.添加该结点到左子树；2.添加该结点到右子树。请输入操作对应的数字。"<<endl;
  do
  {
   cin>>menusel;
   if(menusel=='1'||menusel=='2')
   {
    switch(menusel)
    {
     case '1':     //添加结点到左子树
      if(parent->left)                 //左子树不为空
      {
       cout<<"左子树结点不为空"<<endl;
      }
      else
      {
       parent->left=pnode;
       cout<<"数据添加成功！"<<endl;
      }
      break;
     case '2':     //添加结点到右子树
      if(parent->right)                 //右子树不为空
      {
       cout<<"右子树结点不为空"<<endl;
      }
      else
      {
       parent->right=pnode;
       cout<<"数据添加成功！"<<endl;
      }
      break;
     default:
      cout<<"子节点选择error!"<<endl;
      break;
    }
   }
  }while(menusel!='1'&&menusel!='2');
 }
}
/***********************计算二叉树的深度********************************/
int TreeDepth(CBTType *treeNode)
{
 int depleft,depright;
 if(treeNode==NULL)
 {
  return 0;     //结点为空的时候，深度为0
 }
 else
 {
  depleft=TreeDepth(treeNode->left);  //左子树深度（递归调用）
  depright=TreeDepth(treeNode->right);        //右子树深度（递归调用）
  if(depleft)
  {
   return ++depleft;
  }
  else
  {
   return ++depright;
  }
 }
}
/*************************显示结点数据*********************************/
void ShowNodeData(CBTType *treeNode)
{
 cout<<treeNode->data<<"\t";     //直接输出结点数据
}
/***********************清空二叉树************************************/
void ClearTree(CBTType *treeNode)
{
 if(treeNode)       //判断当前树不为空
 {
  ClearTree(treeNode->left);    //清空左子树
  ClearTree(treeNode->right);    //清空右子树
  delete treeNode;     //释放当前结点所占用的内存 
 }
}
/**************************按层遍历算法*********************************/
void LevelTree(CBTType *treeNode)
{
 CBTType *p;
 CBTType *q[MAXLEN];      //定义一个队列
 int head=0,tail=0;
 if(treeNode)       //如果队首指针不为空
 {
  tail=(tail+1)%MAXLEN;     //计算循环队列队尾序号
  q[tail]=treeNode;     //二叉树根指针进入队列
  while(head!=tail)
  {
   head=(head+1)%MAXLEN;    //计算循环队列的队首序号
   p=q[head];     //获取队首元素
   ShowNodeData(p);    //输出队首元素
   if(p->left!=NULL)    //如果存在左子树
   {
    tail=(tail+1)%MAXLEN;   //计算队列的队尾序号
    q[tail]=p->left;   //左子树入队
   }
   if(p->right!=NULL)    //如果存在右子树
   {
    tail=(tail+1)%MAXLEN;   //计算队列的队尾序号
    q[tail]=p->right;   //右子树入队
   }
  }
 }
}
/*************************先序遍历算法**********************************/
void DLRTree(CBTType *treeNode)
{
 if(treeNode)
 {
  ShowNodeData(treeNode);     //显示结点内容
  DLRTree(treeNode->left);    //显示左子树内容
  DLRTree(treeNode->right);    //显示右子树内容
 }
}
/***********************中序遍历算法************************************/
void LDRTree(CBTType *treeNode)
{
 if(treeNode)
 {

LDRTree(treeNode->left);    //显示左子树内容   
  ShowNodeData(treeNode);     //显示结点内容
  DLRTree(treeNode->right);    //显示右子树内容    
 } 
}
/***********************后序遍历算法************************************/
void LRDTree(CBTType *treeNode)
{
 if(treeNode)
 {
  LRDTree(treeNode->left);    //显示左子树内容 
  DLRTree(treeNode->right);    //显示右子树内容    
  ShowNodeData(treeNode);     //显示结点内容
 } 
}
/*************************主函数部分************************************/
int main()
{
 CBTType *root=NULL;      //root为指向二叉树根结点的指针
 char menusel;
 //设置根结点
 root=InitTree();
 //添加结点
 do
 {
  cout<<"请选择菜单添加二叉树的结点："<<endl;
  cout<<"0.退出;1.添加二叉树的结点。"<<endl;
  cin>>menusel;
  switch(menusel)
  {
   case '1':
    AddTreeNode(root);
    break;
   case '0':
    break;
   default:
    cout<<"添加结点error"<<endl;
    break;
  }
 }while(menusel!='0');
 //输出树的深度
 cout<<"depth:"<<TreeDepth(root)<<endl;
 //输出结点内容
 do
 {
  cout<<"请选择菜单遍历二叉树，输入0表示退出："<<endl;
  cout<<"1.按层遍历"<<endl;
  cout<<"2.先序遍历DLR"<<endl;
  cout<<"3.中序遍历LDR"<<endl;
  cout<<"4.后序遍历LRD"<<endl;
  cin>>menusel;
  switch(menusel)
  {
   case '0':break;
    case '1':
     cout<<"按层遍历的结果："<<endl;
     LevelTree(root);
       cout<<endl;
    break;
   case '2':
    cout<<"先序遍历的结果："<<endl;
    DLRTree(root);
    cout<<endl;
    break;
   case '3':
    cout<<"中序遍历的结果："<<endl;
    LDRTree(root);
    cout<<endl;
    break; 
   case '4':
    cout<<"后序遍历的结果："<<endl;
    LRDTree(root);
    cout<<endl;
    break;
   default:
    cout<<"遍历方式选择出错！"<<endl;
    break;
  }
 }while(menusel!='0');
 //清空二叉树 
 ClearTree(root);
 return 0; 
}

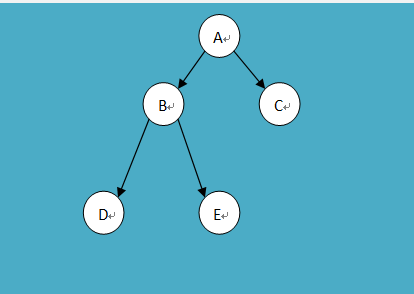
对应的树形结构图如图：

程序运行界面：