Java 数据结构与算法系列精讲之红黑树

目录

• 概述
• 红黑树
• 红黑树的实现
• Node类
• 添加元素
• 左旋
• 右旋
• 完整代码

概述

从今天开始, 小白我将带大家开启 Java 数据结构 & 算法的新篇章.

红黑树

红黑树 (Red Black Tree) 是一种自平衡二叉查找树. 如图:

红黑树的特征:

• 研究红黑树的每个节点都是由颜色的, 非黑即红
• 根节点为黑色
• 每个叶子节点都是黑色的
• 如果一个子节点是红色的, 那么它的孩子节点都是黑色的
• 从任何一个节点到叶子节点, 经过的黑色节点是一样的

红黑树的实现

Node 类

// Node类
private class Node {
    public E e;
    public Node left;
    public Node right;
    public boolean color;

    // Node构造
    public Node(E e) {
        this.e = e;
        this.left = null;
        this.right = null;
        color = RED;
    }

    @Override
    public String toString() {
        return "It is node value is: " + e;
    }
}

添加元素

// 添加元素
public Node addElement(Node node, E e) {

    if(node == null) {
        size++;
        return new Node(e);
    }

    // 判断元素大小
    if(e.compareTo(node.e) < 0) {

        // 左添加
        node.left = addElement(node.left, e);
    } else {

        // 右添加
        node.right = addElement(node.right, e);
    }

    // 左旋
    if(isRed(node.right) && !isRed(node.left)) {
        node = leftRotate(node);
    }

    // 右旋
    if(isRed(node.left) && !isRed(node.left.left)) {
        node = rightRotate(node);
   }

    // 颜色反转
    if(isRed(node.right) && !isRed(node.left)) {
        flipColors(node);
    }

    return node;
}

左旋

左旋指的是, 以某个节点作为支撑点, 其右子节点变为旋转节点的父节点, 右子节点的左子节点的左字节点变为旋转节点的右子节点, 旋转节点的左子节点保持不变. 如图:

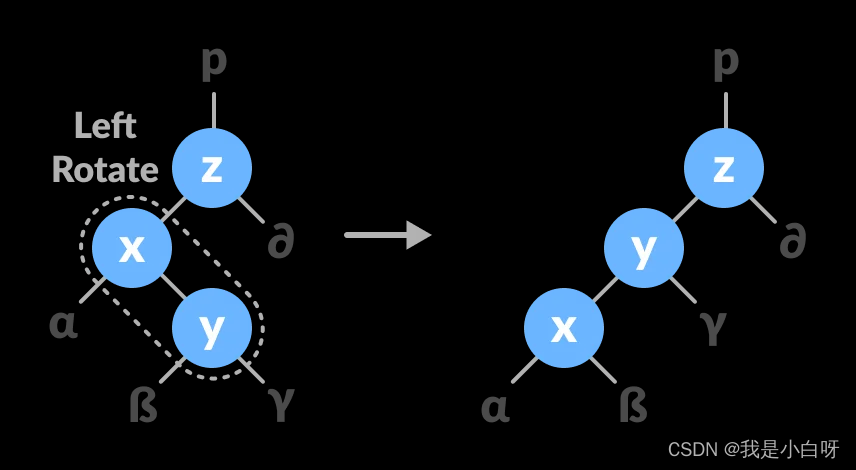
//    node               x
//   /    \    左旋转   /  \
//  T1     x    ==>  node T3
//        /  \       / \
//       T2  T3     T1 T2
private Node leftRotate(Node node) {
    Node x = node.right;

    // 左旋转
    node.right = x.left;
    x.left = node;

    x.color = node.color;
    node.color = RED;

    return x;
}

右旋

右旋与左旋相反.

代码实现:

//        node               x
//       /    \    右旋转   /  \
//      x     T2    ==>   y   node
//    /  \                   /  \
//   y   T1                 T1  T2
private Node rightRotate(Node node) {
   Node x = node.left;

    // 右旋转
    node.left = x.right;
    x.right = node;

    x.color = node.color;
    node.color = RED;

    return x;
}

完整代码

public class RBT<E extends Comparable<E>> {

    private static final boolean RED = true;
    private static final boolean BLACK = true;

    // Node类
    private class Node {
        public E e;
        public Node left;
        public Node right;
        public boolean color;

        // Node构造
        public Node(E e) {
            this.e = e;
            this.left = null;
            this.right = null;
            color = RED;
        }

        @Override
        public String toString() {
            return "It is node value is: " + e;
        }
    }

    public Node root;
    private int size;
    public int size() {
        return size;
    }

    // 添加元素
    public Node addElement(Node node, E e) {

        if(node == null) {
            size++;
            return new Node(e);
        }

        // 判断元素大小
        if(e.compareTo(node.e) < 0) {

            // 左添加
            node.left = addElement(node.left, e);
        } else {

            // 右添加
            node.right = addElement(node.right, e);
        }

        // 左旋
        if(isRed(node.right) && !isRed(node.left)) {
            node = leftRotate(node);
        }

        // 右旋
        if(isRed(node.left) && !isRed(node.left.left)) {
            node = rightRotate(node);
        }

        // 颜色反转
        if(isRed(node.right) && !isRed(node.left)) {
            flipColors(node);
        }

        return node;
    }

    //    node               x
    //   /    \    左旋转   /  \
    //  T1     x    ==>  node T3
    //        /  \       / \
    //       T2  T3     T1 T2
    private Node leftRotate(Node node) {
        Node x = node.right;

        // 左旋转
        node.right = x.left;
        x.left = node;

        x.color = node.color;
        node.color = RED;

        return x;
    }

    //        node               x
    //       /    \    右旋转   /  \
    //      x     T2    ==>   y   node
    //    /  \                   /  \
    //   y   T1                 T1  T2
    private Node rightRotate(Node node) {
        Node x = node.left;

        // 右旋转
        node.left = x.right;
        x.right = node;

        x.color = node.color;
        node.color = RED;

        return x;
    }

    // 颜色反转
    private void flipColors(Node node) {
        node.color = RED;
        node.left.color = BLACK;
        node.right.color = BLACK;
    }

    // 判断是否为红色
    private boolean isRed(Node node) {
        if(node==null) return BLACK;
        return node.color;
    }
}

到此这篇关于Java 数据结构与算法系列精讲之红黑树的文章就介绍到这了,更多相关Java 红黑树内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！