C++ 匈牙利算法案例分析详解

匈牙利算法是由匈牙利数学家Edmonds于1965年提出，因而得名。匈牙利算法是基于Hall定理中充分性证明的思想，它是部图匹配最常见的算法，该算法的核心就是寻找增广路径，它是一种用增广路径求二分图最大匹配的算法。

-------等等，看得头大？那么请看下面的版本：

通过数代人的努力，你终于赶上了剩男剩女的大潮，假设你是一位光荣的新世纪媒人，在你的手上有N个剩男，M个剩女，每个人都可能对多名异性有好感（-_-||暂时不考虑特殊的性取向），如果一对男女互有好感，那么你就可以把这一对撮合在一起，现在让我们无视掉所有的单相思（好忧伤的感觉），你拥有的大概就是下面这样一张关系图，每一条连线都表示互有好感。

本着救人一命，胜造七级浮屠的原则，你想要尽可能地撮合更多的情侣，匈牙利算法的工作模式会教你这样做：

一： 先试着给1号男生找妹子，发现第一个和他相连的1号女生还名花无主，got it，连上一条蓝线

二：接着给2号男生找妹子，发现第一个和他相连的2号女生名花无主，got it

三：接下来是3号男生，很遗憾1号女生已经有主了，怎么办呢？

我们试着给之前1号女生匹配的男生（也就是1号男生）另外分配一个妹子。

(黄色表示这条边被临时拆掉)

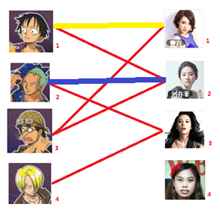
与1号男生相连的第二个女生是2号女生，但是2号女生也有主了，怎么办呢？我们再试着给2号女生的原配重新找个妹子(注意这个步骤和上面是一样的，这是一个递归的过程)

此时发现2号男生还能找到3号女生，那么之前的问题迎刃而解了，回溯回去

2号男生可以找3号妹子~~~                  1号男生可以找2号妹子了~~~                3号男生可以找1号妹子

所以第三步最后的结果就是：

四： 接下来是4号男生，很遗憾，按照第三步的节奏我们没法给4号男生腾出来一个妹子，我们实在是无能为力了……香吉士同学走好。

这就是匈牙利算法的流程，其中找妹子是个递归的过程，最最关键的字就是“ 腾”字

其原则大概是：有机会上，没机会创造机会也要上

【code】

[cpp]  view plain  copy

bool find(int x){
    int i,j;
    for (j=1;j<=m;j++){    //扫描每个妹子
        if (line[x][j]==true && used[j]==false)
        //如果有暧昧并且还没有标记过(这里标记的意思是这次查找曾试图改变过该妹子的归属问题，但是没有成功，所以就不用瞎费工夫了）
        {
            used[j]=1;
            if (girl[j]==0 || find(girl[j])) {
                //名花无主或者能腾出个位置来，这里使用递归
                girl[j]=x;
                return true;
            }
        }
    }
    return false;
}

在主程序我们这样做：每一步相当于我们上面描述的一二三四中的一步

for (i=1;i<=n;i++)
{
    memset(used,0,sizeof(used));    //这个在每一步中清空
    if find(i) all+=1;
}

到此这篇关于C++ 匈牙利算法案例分析详解的文章就介绍到这了,更多相关C++ 匈牙利算法内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！

赞 (0)

相关推荐

  • C++实现算法两个数字相加详解

    Add Two Numbers 两个数字相加 You have two numbers represented by a linked list, where each node contains a single digit. The digits are stored in reverse order, such that the 1's digit is at the head of the list. Write a function that adds the two numbers

  • 详解C++实现匈牙利算法

    详解C++实现匈牙利算法

    目录 一.匈牙利算法介绍 二.最大匹配问题 三.最小点覆盖问题 四.匈牙利算法的应用 4.1.(洛谷P1129) [ZJOI2007]矩阵游戏 4.2.(vijos1204) CoVH之柯南开锁 4.3.(TYVJ P1035) 棋盘覆盖 一.匈牙利算法介绍 匈牙利算法(Hungarian algorithm)主要用于解决一些与二分图匹配有关的问题,所以我们先来了解一下二分图. 二分图(Bipartite graph)是一类特殊的图,它可以被划分为两个部分,每个部分内的点互不相连.下图是典型的二

  • 详解C++实现拓扑排序算法

    详解C++实现拓扑排序算法

    一.拓扑排序的介绍 拓扑排序对应施工的流程图具有特别重要的作用,它可以决定哪些子工程必须要先执行,哪些子工程要在某些工程执行后才可以执行.为了形象地反映出整个工程中各个子工程(活动)之间的先后关系,可用一个有向图来表示,图中的顶点代表活动(子工程),图中的有向边代表活动的先后关系,即有向边的起点的活动是终点活动的前序活动,只有当起点活动完成之后,其终点活动才能进行.通常,我们把这种顶点表示活动.边表示活动间先后关系的有向图称做顶点活动网(Activity On Vertex network),简

  • c++ Bellman-Ford算法的具体实现

    c++ Bellman-Ford算法的具体实现

    Bellman-Ford算法用于解决有边数限制的最短路问题,且可以应对有负边权的图 其时间复杂度为O(nm),效率较低 代码实现: #include<iostream> #include<cstring> #include<algorithm> #define inf 0x3f3f3f3f using namespace std; const int N=1e4+10; const int M=510; int m,n,k,dis[M],backup[M]; //m条边

  • C/C++ 常用排序算法整理汇总分享

    (伪)冒泡排序算法: 相邻的两个元素之间,如果反序则交换数值,直到没有反序的记录为止. #include <stdio.h> void BubbleSort(int Array[], int ArraySize) { int x, y, temporary; for (x = 0; x < ArraySize - 1; x++) { for (y = x + 1; y < ArraySize; y++) { if (Array[x] > Array[y]) { tempora

  • 详解C++实现链表的排序算法

    详解C++实现链表的排序算法

    一.链表排序 最简单.直接的方式(直接采用冒泡或者选择排序,而且不是交换结点,只交换数据域) //线性表的排序,采用冒泡排序,直接遍历链表 void Listsort(Node* & head) { int i = 0; int j = 0; //用于变量链表 Node * L = head; //作为一个临时量 Node * p; Node * p1; //如果链表为空直接返回 if (head->value == 0)return; for (i = 0; i < head->

  • 如何用C++实现A*寻路算法

    如何用C++实现A*寻路算法

    目录 一.A*算法介绍 二.A*算法步骤解析 三.A*算法优化思路 3.1.openList使用优先队列(二叉堆) 3.2.障碍物列表,closeList 使用二维表(二维数组) 3.3.深度限制 四.A*算法实现(C++代码) 一.A*算法介绍 寻路,即找到一条从某个起点到某个终点的可通过路径.而因为实际情况中,起点和终点之间的直线方向往往有障碍物,便需要一个搜索的算法来解决. 有一定算法基础的同学可能知道从某个起点到某个终点通常使用深度优先搜索(DFS),DFS搜索的搜索方向一般是8个方向(

  • C++中实现OpenCV图像分割与分水岭算法

    C++中实现OpenCV图像分割与分水岭算法

    分水岭算法是一种图像区域分割法,在分割的过程中,它会把跟临近像素间的相似性作为重要的参考依据,从而将在空间位置上相近并且灰度值相近的像素点互相连接起来构成一个封闭的轮廓,封闭性是分水岭算法的一个重要特征. API介绍 void watershed( InputArray image, InputOutputArray markers ); 参数说明: image: 必须是一个8bit 3通道彩色图像矩阵序列 markers: 在执行分水岭函数watershed之前,必须对第二个参数markers

  • C++ 匈牙利算法案例分析详解

    C++ 匈牙利算法案例分析详解

    匈牙利算法是由匈牙利数学家Edmonds于1965年提出,因而得名.匈牙利算法是基于Hall定理中充分性证明的思想,它是部图匹配最常见的算法,该算法的核心就是寻找增广路径,它是一种用增广路径求二分图最大匹配的算法. -------等等,看得头大?那么请看下面的版本: 通过数代人的努力,你终于赶上了剩男剩女的大潮,假设你是一位光荣的新世纪媒人,在你的手上有N个剩男,M个剩女,每个人都可能对多名异性有好感(-_-||暂时不考虑特殊的性取向),如果一对男女互有好感,那么你就可以把这一对撮合在一起,现在

  • Java AbstractMethodError案例分析详解

    Java AbstractMethodError案例分析详解

    背景 AbstractMethodError异常对于我来说还是比较不常遇见的,最近有幸遇到,并侥幸的解决了,在这里把此种场景剖析一番,进入正题,下面是AbstractMethodError在Java的异常机制中所处的位置: 现在明确了AbstractMethodError所具有的特性: 1.它是Error的子类,Error类及其子类都是被划分在非检查异常之列的,就是说这些异常不能在编译阶段被检查出来,只能在运行时才会触发. 2.通过API文档里面的解释大致得出的结论就是说A依赖于B,但是执行的时

  • python机器学习算法与数据降维分析详解

    python机器学习算法与数据降维分析详解

    目录 一.数据降维 1.特征选择 2.主成分分析(PCA) 3.降维方法使用流程 二.机器学习开发流程 1.机器学习算法分类 2.机器学习开发流程 三.转换器与估计器 1.转换器 2.估计器 一.数据降维 机器学习中的维度就是特征的数量,降维即减少特征数量.降维方式有:特征选择.主成分分析. 1.特征选择 当出现以下情况时,可选择该方式降维: ①冗余:部分特征的相关度高,容易消耗计算性能 ②噪声:部分特征对预测结果有影响 特征选择主要方法:过滤式(VarianceThreshold).嵌入式(正

  • Java逃逸分析详解及代码示例

    概念引入 我们都知道,Java 创建的对象都是被分配到堆内存上,但是事实并不是这么绝对,通过对Java对象分配的过程分析,可以知道有两个地方会导致Java中创建出来的对象并一定分别在所认为的堆上.这两个点分别是Java中的逃逸分析和TLAB(Thread Local Allocation Buffer)线程私有的缓存区. 基本概念介绍 逃逸分析,是一种可以有效减少Java程序中同步负载和内存堆分配压力的跨函数全局数据流分析算法.通过逃逸分析,Java Hotspot编译器能够分析出一个新的对象的

  • 使用 Node.js 实现图片的动态裁切及算法实例代码详解

    背景&概览 目前常见的图床服务都会有图片动态裁切的功能,主要的应用场景用以为各种终端和业务形态输出合适尺寸的图片. 一张动辄以 MB 为计量单位的原始大图,通常不会只设置一下显示尺寸就直接输出到终端中,因为体积太大加载体验会很差,除了影响加载速度还会增加终端设备的内存占用.所以要想在各种终端下都能保证图片质量的同时又确保输出合适的尺寸,那么此时就需要根据图片 URL 来对原始图片进行裁切,然后动态生成并输出一张新的图片. URL 的设计 图片 URL 需要包含图片 id.尺寸.质量等信息.有两种

  • R语言关于随机森林算法的知识点详解

    在随机森林方法中,创建大量的决策树. 每个观察被馈入每个决策树. 每个观察的最常见的结果被用作最终输出. 新的观察结果被馈入所有的树并且对每个分类模型取多数投票. 对构建树时未使用的情况进行错误估计. 这称为OOB(袋外)误差估计,其被提及为百分比. R语言包"randomForest"用于创建随机森林. 安装R包 在R语言控制台中使用以下命令安装软件包. 您还必须安装相关软件包(如果有). install.packages("randomForest") 包&qu

  • java数组算法例题代码详解(冒泡排序,选择排序,找最大值、最小值,添加、删除元素等)

    java数组算法例题代码详解(冒泡排序,选择排序,找最大值、最小值,添加、删除元素等)

    数组算法例题 1.数组逆序 第一个和最后一个互换,第二个和倒数第二个互换,就相当于把数组想下图一样,进行对折互换,如果数组个数为奇数,则中间保持不变其余元素互换即可 import java.util.Arrays; class Demo12 { public static void main (String[] args) { int[] arr = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}; System.out.println(Arrays.toString(arr));

  • Python数据结构与算法之算法分析详解

    Python数据结构与算法之算法分析详解

    目录 0. 学习目标 1. 算法的设计要求 1.1 算法评价的标准 1.2 算法选择的原则 2. 算法效率分析 2.1 大O表示法 2.2 常见算法复杂度 2.3 复杂度对比 3. 算法的存储空间需求分析 4. Python内置数据结构性能分析 4.1 列表性能分析 4.2 字典性能分析 0. 学习目标 我们已经知道算法是具有有限步骤的过程,其最终的目的是为了解决问题,而根据我们的经验,同一个问题的解决方法通常并非唯一.这就产生一个有趣的问题:如何对比用于解决同一问题的不同算法?为了以合理的方式

  • jvm垃圾回收之GC调优工具分析详解

    jvm垃圾回收之GC调优工具分析详解

    进行GC性能调优时, 需要明确了解, 当前的GC行为对系统和用户有多大的影响.有多种监控GC的工具和方法, 本章将逐一介绍常用的工具. JVM 在程序执行的过程中, 提供了GC行为的原生数据.那么, 我们就可以利用这些原生数据来生成各种报告.原生数据(raw data) 包括: 各个内存池的当前使用情况, 各个内存池的总容量, 每次GC暂停的持续时间, GC暂停在各个阶段的持续时间. 可以通过这些数据算出各种指标, 例如: 程序的内存分配率, 提升率等等.本章主要介绍如何获取原生数据. 后续的章

  • YGC前后新生代是否变大分析详解

    问题描述 我们都知道gc是为了释放内存,但是你是否碰到过ygc前后新生代反增不减的情况呢?gc日志效果类似下面的: 2016-05-18T15:06:13.011+0800: [GC [ParNew (promotion failed): 636088K->690555K(707840K), 0.2958900 secs][CMS: 1019739K->1019733K(1310720K), 2.6208600 secs] 1655820K->1655820K(2018560K), [C

随机推荐