利用Python实现最小二乘法与梯度下降算法

导入所需库

%matplotlib inline
import sympy
import numpy as np
import matplotlib.pyplot as plt
from sympy.abc import x as a,y as b

生成模拟数据

# 模拟函数 y=3x-1

#自变量
x=np.linspace(-5,5,num=1000)
#加入噪声
noise=np.random.rand(len(x))*2-1
#因变量
y=3*x-1+noise

查看所生成数据的图像

plt.figure(figsize=(10,10))
plt.scatter(x,y,s=1)

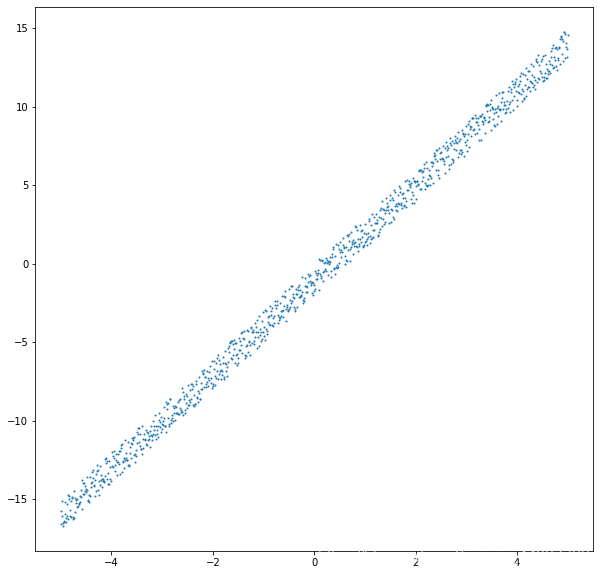
求代价函数的偏导

y=ax+b  #目标函数

e=1/2*Σ([axi+b]-yi)^2   #代价函数，求使得代价函数为最小值时，对应的a和b

对a求偏导->Σ(axi+b-yi)*xi

对b求偏导->Σ(axi+b-yi)

1. 通过最小二乘法求a，b

我们知道当在a,b处的偏导为0时，代价函数e达到最小值，所以得到二元一次方程组

Σ(axi+b-yi)*xi=0
Σ(axi+b-yi)=0

该方程组是关于未知数为a,b的二元一次方程组，通过求解该方程，得到a，b

result=sympy.solve([
  np.sum((a*x+b-y)*x),
  np.sum(a*x+b-y)],[a,b])
print(result)	#{x: 3.01182977621975, y: -1.00272253325765}

通过sympy库解方程组，得出了a= 3.01182977621975，b= -1.00272253325765，已经与我们真实的a，b很接近了，下面进行作图

plt.figure(figsize=(10,10))
plt.scatter(x,y,s=1)
plt.plot(x,result[a]*x+result[b],c='red')

print(type(a),type(b))	#<class 'sympy.core.symbol.Symbol'> <class 'sympy.core.symbol.Symbol'>

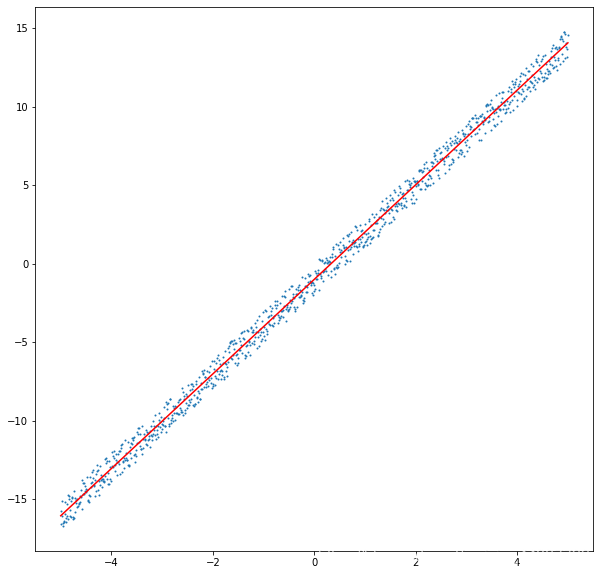
2. 通过梯度下降算法求a，b

我们注意到最小二乘法最后一步要求p个方程组，是非常大的计算量，其实计算起来很难，因此我们就有了一种新的计算方法，就是梯度下降法，梯度下降法可以看作是 更简单的一种 求最小二乘法最后一步解方程 的方法

# 注意这里覆盖了sympy.abc的a和b
# 设定a和b的起始点
a,b=0.1,0.1

#步长，也称作学习率
alpha=0.00001

#循环一千次结束
for i in range(1000):
  a-=alpha*np.sum((a*x+b-y)*x)
  b-=alpha*np.sum(a*x+b-y)

print(a,b)	#3.0118297762197526 -1.002674927350334

通过梯度下降法，得出了a= 3.0118297762197526，b= -1.002674927350334，也是很接近真实的a，b值了，作图看看

plt.figure(figsize=(10,10))
plt.scatter(x,y,s=1)
plt.plot(x,a*x+b,c='black')

print(type(a),type(b))	#<class 'numpy.float64'> <class 'numpy.float64'>

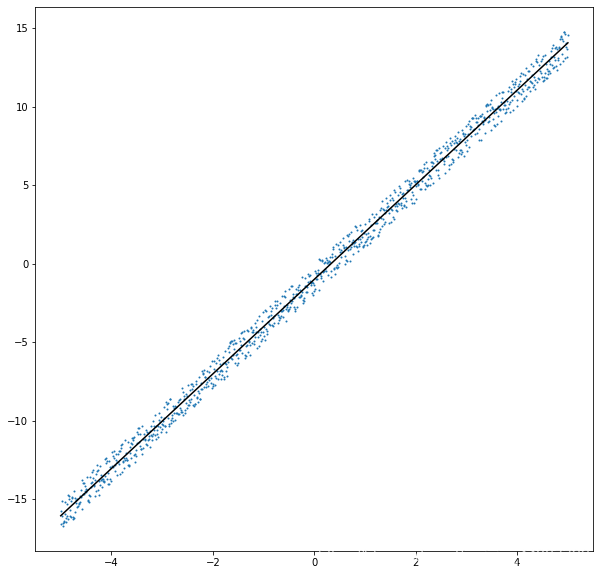
到此这篇关于利用Python实现最小二乘法与梯度下降算法的文章就介绍到这了,更多相关Python最小二乘法与梯度下降内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！

赞 (0)

相关推荐

  • Python基于最小二乘法实现曲线拟合示例

    Python基于最小二乘法实现曲线拟合示例

    本文实例讲述了Python基于最小二乘法实现曲线拟合.分享给大家供大家参考,具体如下: 这里不手动实现最小二乘,调用scipy库中实现好的相关优化函数. 考虑如下的含有4个参数的函数式: 构造数据 import numpy as np from scipy import optimize import matplotlib.pyplot as plt def logistic4(x, A, B, C, D): return (A-D)/(1+(x/C)**B)+D def residuals(p

  • Python 普通最小二乘法(OLS)进行多项式拟合的方法

    多元函数拟合.如 电视机和收音机价格多销售额的影响,此时自变量有两个. python 解法: import numpy as np import pandas as pd #import statsmodels.api as sm #方法一 import statsmodels.formula.api as smf #方法二 import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D df = pd.read_c

  • 最小二乘法及其python实现详解

    最小二乘法Least Square Method,做为分类回归算法的基础,有着悠久的历史(由马里·勒让德于1806年提出).它通过最小化误差的平方和寻找数据的最佳函数匹配.利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小.最小二乘法还可用于曲线拟合.其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达. 那什么是最小二乘法呢?别着急,我们先从几个简单的概念说起. 假设我们现在有一系列的数据点 ,那么由我们给出的拟合函数h(x)得到的估计量就是

  • python中最小二乘法详细讲解

    python中在实现一元线性回归时会使用最小二乘法,那你知道最小二乘法是什么吗.其实最小二乘法为分类回归算法的基础,从求解线性透视图中的消失点,m元n次函数的拟合,包括后来学到的神经网络,其思想归根结底全都是最小二乘法.本文向大家介绍python中的最小二乘法. 一.最小二乘法是什么 最小二乘法Least Square Method,做为分类回归算法的基础,有着悠久的历史(由马里·勒让德于1806年提出). 二.最小二乘法实现原理 通过最小化误差的平方和寻找数据的最佳函数匹配. 三.最小二乘法功

  • python实现最小二乘法线性拟合

    python实现最小二乘法线性拟合

    本文python代码实现的是最小二乘法线性拟合,并且包含自己造的轮子与别人造的轮子的结果比较. 问题:对直线附近的带有噪声的数据进行线性拟合,最终求出w,b的估计值. 最小二乘法基本思想是使得样本方差最小. 代码中self_func()函数为自定义拟合函数,skl_func()为调用scikit-learn中线性模块的函数. import numpy as np import matplotlib.pyplot as plt from sklearn.linear_model import Li

  • python中matplotlib实现最小二乘法拟合的过程详解

    python中matplotlib实现最小二乘法拟合的过程详解

    前言 最小二乘法Least Square Method,做为分类回归算法的基础,有着悠久的历史(由马里·勒让德于1806年提出).它通过最小化误差的平方和寻找数据的最佳函数匹配.利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小.最小二乘法还可用于曲线拟合.其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达. 下面这篇文章主要跟大家介绍了关于python中matplotlib实现最小二乘法拟合的相关内容,下面话不多说,来一起看看详细的介绍:

  • Python实现曲线拟合的最小二乘法

    本文实例为大家分享了Python曲线拟合的最小二乘法,供大家参考,具体内容如下 模块导入 import numpy as np import gaosi as gs 代码 """ 本函数通过创建增广矩阵,并调用高斯列主元消去法模块进行求解. """ import numpy as np import gaosi as gs shape = int(input('请输入拟合函数的次数:')) x = np.array([0.6,1.3,1.64,1

  • Python中实现最小二乘法思路及实现代码

    Python中实现最小二乘法思路及实现代码

    之所以说"使用"而不是"实现",是因为python的相关类库已经帮我们实现了具体算法,而我们只要学会使用就可以了.随着对技术的逐渐掌握及积累,当类库中的算法已经无法满足自身需求的时候,我们也可以尝试通过自己的方式实现各种算法. 言归正传,什么是"最小二乘法"呢? 定义:最小二乘法(又称最小平方法)是一种数学优化技术,它通过最小化误差的平方和寻找数据的最佳函数匹配. 作用:利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误

  • Python最小二乘法矩阵

    最小二乘法矩阵 #! /usr/bin/env python # -*- coding: utf-8 -*- import numpy as np def calc_left_k_mat(k): """ 获得左侧k矩阵 :param k: :return: """ k_mat = [] for i in range(k + 1): now_line = [] for j in range(k + 1): now_line.append(j + i

  • 利用Python实现最小二乘法与梯度下降算法

    利用Python实现最小二乘法与梯度下降算法

    导入所需库 %matplotlib inline import sympy import numpy as np import matplotlib.pyplot as plt from sympy.abc import x as a,y as b 生成模拟数据 # 模拟函数 y=3x-1 #自变量 x=np.linspace(-5,5,num=1000) #加入噪声 noise=np.random.rand(len(x))*2-1 #因变量 y=3*x-1+noise 查看所生成数据的图像 p

  • python实现梯度下降算法

    python实现梯度下降算法

    梯度下降(Gradient Descent)算法是机器学习中使用非常广泛的优化算法.当前流行的机器学习库或者深度学习库都会包括梯度下降算法的不同变种实现. 本文主要以线性回归算法损失函数求极小值来说明如何使用梯度下降算法并给出python实现.若有不正确的地方,希望读者能指出. 梯度下降 梯度下降原理:将函数比作一座山,我们站在某个山坡上,往四周看,从哪个方向向下走一小步,能够下降的最快. 在线性回归算法中,损失函数为 在求极小值时,在数据量很小的时候,可以使用矩阵求逆的方式求最优的θ值.但当数

  • 梯度下降法介绍及利用Python实现的方法示例

    梯度下降法介绍及利用Python实现的方法示例

    本文主要给大家介绍了梯度下降法及利用Python实现的相关内容,分享出来供大家参考学习,下面话不多说,来一起看看详细的介绍吧. 梯度下降法介绍 梯度下降法(gradient descent),又名最速下降法(steepest descent)是求解无约束最优化问题最常用的方法,它是一种迭代方法,每一步主要的操作是求解目标函数的梯度向量,将当前位置的负梯度方向作为搜索方向(因为在该方向上目标函数下降最快,这也是最速下降法名称的由来). 梯度下降法特点:越接近目标值,步长越小,下降速度越慢. 直观上

  • python梯度下降算法的实现

    本文实例为大家分享了python实现梯度下降算法的具体代码,供大家参考,具体内容如下 简介 本文使用python实现了梯度下降算法,支持y = Wx+b的线性回归 目前支持批量梯度算法和随机梯度下降算法(bs=1) 也支持输入特征向量的x维度小于3的图像可视化 代码要求python版本>3.4 代码 ''' 梯度下降算法 Batch Gradient Descent Stochastic Gradient Descent SGD ''' __author__ = 'epleone' import

  • python使用梯度下降算法实现一个多线性回归

    python使用梯度下降算法实现一个多线性回归,供大家参考,具体内容如下 图示: import pandas as pd import matplotlib.pylab as plt import numpy as np # Read data from csv pga = pd.read_csv("D:\python3\data\Test.csv") # Normalize the data 归一化值 (x - mean) / (std) pga.AT = (pga.AT - pga

  • python应用Axes3D绘图（批量梯度下降算法）

    本文实例为大家分享了python批量梯度下降算法的具体代码,供大家参考,具体内容如下 问题: 将拥有两个自变量的二阶函数绘制到空间坐标系中,并通过批量梯度下降算法找到并绘制其极值点 大体思路: 首先,根据题意确定目标函数:f(w1,w2) = w1^2 + w2^2 + 2 w1 w2 + 500 然后,针对w1,w2分别求偏导,编写主方法求极值点 而后,创建三维坐标系绘制函数图像以及其极值点即可 具体代码实现以及成像结果如下: import numpy as np import matplot

  • python实现梯度下降算法的实例详解

    python版本选择 这里选的python版本是2.7,因为我之前用python3试了几次,发现在画3d图的时候会报错,所以改用了2.7. 数据集选择 数据集我选了一个包含两个变量,三个参数的数据集,这样可以画出3d图形对结果进行验证. 部分函数总结 symbols()函数:首先要安装sympy库才可以使用.用法: >>> x1 = symbols('x2') >>> x1 + 1 x2 + 1 在这个例子中,x1和x2是不一样的,x2代表的是一个函数的变量,而x1代表

  • python 还原梯度下降算法实现一维线性回归

    首先我们看公式: 这个是要拟合的函数 然后我们求出它的损失函数, 注意:这里的n和m均为数据集的长度,写的时候忘了 注意,前面的theta0-theta1x是实际值,后面的y是期望值 接着我们求出损失函数的偏导数: 最终,梯度下降的算法: 学习率一般小于1,当损失函数是0时,我们输出theta0和theta1. 接下来上代码! class LinearRegression(): def __init__(self, data, theta0, theta1, learning_rate): se

  • 图文详解梯度下降算法的原理及Python实现

    图文详解梯度下降算法的原理及Python实现

    目录 1.引例 2.数值解法 3.梯度下降算法 4.代码实战:Logistic回归 1.引例 给定如图所示的某个函数,如何通过计算机算法编程求f(x)min? 2.数值解法 传统方法是数值解法,如图所示 按照以下步骤迭代循环直至最优: ① 任意给定一个初值x0: ② 随机生成增量方向,结合步长生成Δx: ③ 计算比较f(x0)与f(x0+Δx)的大小,若f(x0+Δx)<f(x0)则更新位置,否则重新生成Δx: ④ 重复②③直至收敛到最优f(x)min. 数值解法最大的优点是编程简明,但缺陷也很

  • Python语言描述随机梯度下降法

    Python语言描述随机梯度下降法

    1.梯度下降 1)什么是梯度下降? 因为梯度下降是一种思想,没有严格的定义,所以用一个比喻来解释什么是梯度下降. 简单来说,梯度下降就是从山顶找一条最短的路走到山脚最低的地方.但是因为选择方向的原因,我们找到的的最低点可能不是真正的最低点.如图所示,黑线标注的路线所指的方向并不是真正的地方. 既然是选择一个方向下山,那么这个方向怎么选?每次该怎么走? 先说选方向,在算法中是以随机方式给出的,这也是造成有时候走不到真正最低点的原因. 如果选定了方向,以后每走一步,都是选择最陡的方向,直到最低点.

随机推荐