吴恩达机器学习练习:神经网络(反向传播)

1 Neural Networks 神经网络

1.1 Visualizing the data 可视化数据

这部分我们随机选取100个样本并可视化。训练集共有5000个训练样本，每个样本是20*20像素的数字的灰度图像。每个像素代表一个浮点数，表示该位置的灰度强度。20×20的像素网格被展开成一个400维的向量。在我们的数据矩阵X中，每一个样本都变成了一行，这给了我们一个5000×400矩阵X，每一行都是一个手写数字图像的训练样本。

import numpy as np
import matplotlib.pyplot as plt
from scipy.io import loadmat
import scipy.optimize as opt
from sklearn.metrics import classification_report  # 这个包是评价报告

def load_mat(path):
    '''读取数据'''
    data = loadmat('ex4data1.mat')  # return a dict
    X = data['X']
    y = data['y'].flatten()
    return X, y

def plot_100_images(X):
    """随机画100个数字"""
    index = np.random.choice(range(5000), 100)
    images = X[index]
    fig, ax_array = plt.subplots(10, 10, sharey=True, sharex=True, figsize=(8, 8))
    for r in range(10):
        for c in range(10):
            ax_array[r, c].matshow(images[r*10 + c].reshape(20,20), cmap='gray_r')
    plt.xticks([])
    plt.yticks([])
    plt.show()

X,y = load_mat('ex4data1.mat')
plot_100_images(X)

1.2 Model representation 模型表示

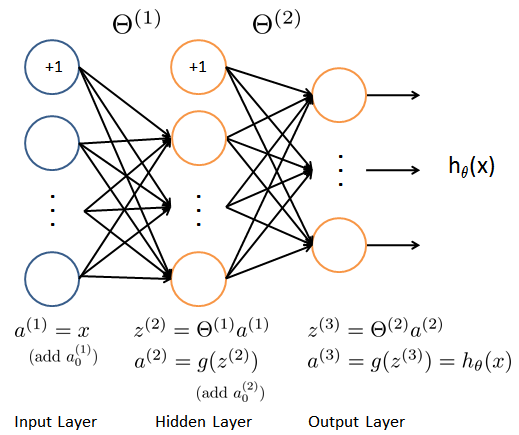
我们的网络有三层，输入层，隐藏层，输出层。我们的输入是数字图像的像素值，因为每个数字的图像大小为20*20，所以我们输入层有400个单元（这里不包括总是输出要加一个偏置单元）。

1.2.1 load train data set 读取数据

首先我们要将标签值（1，2，3，4，…，10）转化成非线性相关的向量，向量对应位置（y[i-1]）上的值等于1，例如y[0]=6转化为y[0]=[0,0,0,0,0,1,0,0,0,0]。

from sklearn.preprocessing import OneHotEncoder
def expand_y(y):
    result = []
    # 把y中每个类别转化为一个向量，对应的lable值在向量对应位置上置为1
    for i in y:
        y_array = np.zeros(10)
        y_array[i-1] = 1
        result.append(y_array)
    '''
    # 或者用sklearn中OneHotEncoder函数
    encoder =  OneHotEncoder(sparse=False)  # return a array instead of matrix
    y_onehot = encoder.fit_transform(y.reshape(-1,1))
    return y_onehot
    '''
    return np.array(result)

获取训练数据集，以及对训练集做相应的处理，得到我们的input X，lables y。

raw_X, raw_y = load_mat('ex4data1.mat')
X = np.insert(raw_X, 0, 1, axis=1)
y = expand_y(raw_y)
X.shape, y.shape
'''
((5000, 401), (5000, 10))
'''
.csdn.net/Cowry5/article/details/80399350

1.2.2 load weight 读取权重

这里我们提供了已经训练好的参数θ1，θ2，存储在ex4weight.mat文件中。这些参数的维度由神经网络的大小决定，第二层有25个单元，输出层有10个单元(对应10个数字类)。

def load_weight(path):
    data = loadmat(path)
    return data['Theta1'], data['Theta2'] 

t1, t2 = load_weight('ex4weights.mat')
t1.shape, t2.shape
# ((25, 401), (10, 26))

1.2.3 展开参数

当我们使用高级优化方法来优化神经网络时，我们需要将多个参数矩阵展开，才能传入优化函数，然后再恢复形状。

def serialize(a, b):
    '''展开参数'''
    return np.r_[a.flatten(),b.flatten()]

theta = serialize(t1, t2)  # 扁平化参数，25*401+10*26=10285
theta.shape  # (10285,)

def deserialize(seq):
    '''提取参数'''
    return seq[:25*401].reshape(25, 401), seq[25*401:].reshape(10, 26)

1.3 Feedforward and cost function 前馈和代价函数 1.3.1 Feedforward

确保每层的单元数，注意输出时加一个偏置单元，s(1)=400+1，s(2)=25+1，s(3)=10。

def sigmoid(z):
    return 1 / (1 + np.exp(-z))

def feed_forward(theta, X,):
    '''得到每层的输入和输出'''
    t1, t2 = deserialize(theta)
    # 前面已经插入过偏置单元，这里就不用插入了
    a1 = X
    z2 = a1 @ t1.T
    a2 = np.insert(sigmoid(z2), 0, 1, axis=1)
    z3 = a2 @ t2.T
    a3 = sigmoid(z3)
    return a1, z2, a2, z3, a3

a1, z2, a2, z3, h = feed_forward(theta, X)

1.3.2 Cost function

回顾下神经网络的代价函数（不带正则化项）

输出层输出的是对样本的预测，包含5000个数据，每个数据对应了一个包含10个元素的向量，代表了结果有10类。在公式中，每个元素与log项对应相乘。

最后我们使用提供训练好的参数θ，算出的cost应该为0.287629

def cost(theta, X, y):
    a1, z2, a2, z3, h = feed_forward(theta, X)
    J = 0
    for i in range(len(X)):
        first = - y[i] * np.log(h[i])
        second = (1 - y[i]) * np.log(1 - h[i])
        J = J + np.sum(first - second)
    J = J / len(X)
    return J
'''
     # or just use verctorization
     J = - y * np.log(h) - (1 - y) * np.log(1 - h)
     return J.sum() / len(X)
'''

cost(theta, X, y) # 0.2876291651613189

1.4 Regularized cost function 正则化代价函数

注意不要将每层的偏置项正则化。

最后You should see that the cost is about 0.383770

def regularized_cost(theta, X, y, l=1):
    '''正则化时忽略每层的偏置项，也就是参数矩阵的第一列'''
    t1, t2 = deserialize(theta)
    reg = np.sum(t1[:,1:] ** 2) + np.sum(t2[:,1:] ** 2)  # or use np.power(a, 2)
    return l / (2 * len(X)) * reg + cost(theta, X, y)

regularized_cost(theta, X, y, 1) # 0.38376985909092354

2 Backpropagation 反向传播

2.1 Sigmoid gradient S函数导数

这里可以手动推导，并不难。

def sigmoid_gradient(z):
    return sigmoid(z) * (1 - sigmoid(z))

2.2 Random initialization 随机初始化

当我们训练神经网络时，随机初始化参数是很重要的，可以打破数据的对称性。一个有效的策略是在均匀分布(−e，e)中随机选择值，我们可以选择 e = 0.12 这个范围的值来确保参数足够小，使得训练更有效率。

def random_init(size):
    '''从服从的均匀分布的范围中随机返回size大小的值'''
    return np.random.uniform(-0.12, 0.12, size)

2.3 Backpropagation 反向传播

目标：获取整个网络代价函数的梯度。以便在优化算法中求解。

这里面一定要理解正向传播和反向传播的过程，才能弄清楚各种参数在网络中的维度，切记。比如手写出每次传播的式子。

print('a1', a1.shape,'t1', t1.shape)
print('z2', z2.shape)
print('a2', a2.shape, 't2', t2.shape)
print('z3', z3.shape)
print('a3', h.shape)
'''
a1 (5000, 401) t1 (25, 401)
z2 (5000, 25)
a2 (5000, 26) t2 (10, 26)
z3 (5000, 10)
a3 (5000, 10)
'''

def gradient(theta, X, y):
    '''
    unregularized gradient, notice no d1 since the input layer has no error
    return 所有参数theta的梯度，故梯度D(i)和参数theta(i)同shape，重要。
    '''
    t1, t2 = deserialize(theta)
    a1, z2, a2, z3, h = feed_forward(theta, X)
    d3 = h - y # (5000, 10)
    d2 = d3 @ t2[:,1:] * sigmoid_gradient(z2)  # (5000, 25)
    D2 = d3.T @ a2  # (10, 26)
    D1 = d2.T @ a1 # (25, 401)
    D = (1 / len(X)) * serialize(D1, D2)  # (10285,)
    return D

2.4 Gradient checking 梯度检测

在你的神经网络,你是最小化代价函数J(Θ)。执行梯度检查你的参数,你可以想象展开参数Θ(1)Θ(2)成一个长向量θ。通过这样做,你能使用以下梯度检查过程。

def gradient_checking(theta, X, y, e):
    def a_numeric_grad(plus, minus):
        """
        对每个参数theta_i计算数值梯度，即理论梯度。
        """
        return (regularized_cost(plus, X, y) - regularized_cost(minus, X, y)) / (e * 2)
    numeric_grad = []
    for i in range(len(theta)):
        plus = theta.copy()  # deep copy otherwise you will change the raw theta
        minus = theta.copy()
        plus[i] = plus[i] + e
        minus[i] = minus[i] - e
        grad_i = a_numeric_grad(plus, minus)
        numeric_grad.append(grad_i)
    numeric_grad = np.array(numeric_grad)
    analytic_grad = regularized_gradient(theta, X, y)
    diff = np.linalg.norm(numeric_grad - analytic_grad) / np.linalg.norm(numeric_grad + analytic_grad)
    print('If your backpropagation implementation is correct,\nthe relative difference will be smaller than 10e-9 (assume epsilon=0.0001).\nRelative Difference: {}\n'.format(diff))

gradient_checking(theta, X, y, epsilon= 0.0001)#这个运行很慢，谨慎运行

2.5 Regularized Neural Networks 正则化神经网络

def regularized_gradient(theta, X, y, l=1):
    """不惩罚偏置单元的参数"""
    a1, z2, a2, z3, h = feed_forward(theta, X)
    D1, D2 = deserialize(gradient(theta, X, y))
    t1[:,0] = 0
    t2[:,0] = 0
    reg_D1 = D1 + (l / len(X)) * t1
    reg_D2 = D2 + (l / len(X)) * t2
    return serialize(reg_D1, reg_D2)

2.6 Learning parameters using fmincg 优化参数

def nn_training(X, y):
    init_theta = random_init(10285)  # 25*401 + 10*26
    res = opt.minimize(fun=regularized_cost,
                       x0=init_theta,
                       args=(X, y, 1),
                       method='TNC',
                       jac=regularized_gradient,
                       options={'maxiter': 400})
    return res

res = nn_training(X, y)#慢
res
'''
     fun: 0.5156784004838036
     jac: array([-2.51032294e-04, -2.11248326e-12,  4.38829369e-13, ...,
        9.88299811e-05, -2.59923586e-03, -8.52351187e-04])
 message: 'Converged (|f_n-f_(n-1)| ~= 0)'
    nfev: 271
     nit: 17
  status: 1
 success: True
       x: array([ 0.58440213, -0.02013683,  0.1118854 , ..., -2.8959637 ,
        1.85893941, -2.78756836])
'''

def accuracy(theta, X, y):
    _, _, _, _, h = feed_forward(res.x, X)
    y_pred = np.argmax(h, axis=1) + 1
    print(classification_report(y, y_pred))

accuracy(res.x, X, raw_y)
'''
             precision    recall  f1-score   support
          1       0.97      0.99      0.98       500
          2       0.98      0.97      0.98       500
          3       0.98      0.95      0.96       500
          4       0.98      0.97      0.97       500
          5       0.97      0.98      0.97       500
          6       0.99      0.98      0.98       500
          7       0.99      0.97      0.98       500
          8       0.96      0.98      0.97       500
          9       0.97      0.98      0.97       500
         10       0.99      0.99      0.99       500
avg / total       0.98      0.98      0.98      5000
'''

3 Visualizing the hidden layer 可视化隐藏层

理解神经网络是如何学习的一个很好的办法是，可视化隐藏层单元所捕获的内容。通俗的说，给定一个的隐藏层单元，可视化它所计算的内容的方法是找到一个输入x，x可以激活这个单元（也就是说有一个激活值接近与1）。对于我们所训练的网络，注意到θ1中每一行都是一个401维的向量，代表每个隐藏层单元的参数。如果我们忽略偏置项，我们就能得到400维的向量，这个向量代表每个样本输入到每个隐层单元的像素的权重。因此可视化的一个方法是，reshape这个400维的向量为（20，20）的图像然后输出。

注：

It turns out that this is equivalent to finding the input that gives the highest activation for the hidden unit, given a norm constraint on the input.

这相当于找到了一个输入，给了隐层单元最高的激活值，给定了一个输入的标准限制。例如(||x||2​≤1)

(这部分暂时不太理解)

def plot_hidden(theta):
    t1, _ = deserialize(theta)
    t1 = t1[:, 1:]
    fig,ax_array = plt.subplots(5, 5, sharex=True, sharey=True, figsize=(6,6))
    for r in range(5):
        for c in range(5):
            ax_array[r, c].matshow(t1[r * 5 + c].reshape(20, 20), cmap='gray_r')
            plt.xticks([])
            plt.yticks([])
    plt.show()

plot_hidden(res.x)

到此在这篇练习中，你将学习如何用反向传播算法来学习神经网络的参数，更多相关机器学习，神经网络内容请搜索我们以前的文章或继续浏览下面的相关文章，希望大家以后多多支持我们！