Python OpenCV高斯金字塔与拉普拉斯金字塔的实现

基础知识铺垫

学习图像金字塔，发现网上的资料比较多，检索起来比较轻松。

图像金字塔是一张图像多尺度的表达，或者可以理解成一张图像不同分辨率展示。

金字塔越底层的图片，像素越高，越向上，像素逐步降低，分辨率逐步降低。

高斯金字塔

我们依旧不对概念做过多解释，第一遍学习应用，应用，毕竟 365 天的周期，时间长，后面补充理论知识。

高斯金字塔用于向下采样，同时它也是最基本的图像塔。

在互联网检索原理，得到最简单的说明如下：

将图像的最底层（高斯金字塔的第 0 层），例如高斯核（5x5）对其进行卷积操作，这里的卷积主要处理掉的是偶数行与列，然后得到金字塔上一层图像（即高斯金字塔第 1 层），在针对该图像重复卷积操作，得到第 2 层，反复执行下去，即可得到高斯金字塔。

每次操作之后，都会将 M×N 图像变成 M/2 × N/2 图像，即减少一半。

还有实测中发现，需要用图像的宽和高一致的图片，并且宽高要是 2 的次幂数，例如，8 像素，16 像素，32 像素等等，一会你也可以实际测试一下。

图像金字塔应用到的函数有 cv2.pyrDown() 和 cv2.pyrUp() 。

cv2.pyrDown 与 cv2.pyrUp 函数原型

通过 help 函数得到函数原型如下：

pyrDown(src[, dst[, dstsize[, borderType]]]) -> dst
pyrUp(src[, dst[, dstsize[, borderType]]]) -> dst

两个函数原型参数一致，参数说明如下：

• src：输入图像；
• dst： 输出图像；
• dstsize： 输出图像尺寸，默认值按照 ((src.cols+1)/2, (src.rows+1)/2) 计算。

关于两个函数的补充说明：

• cv2.pyrDown 从一个相对高分辨率的大尺寸的图像上构建一个金字塔，运行之后的结果是，图像变小，分辨率降低（下采样）；
• cv2.pyrUp 是一个上采样的过程，尽管相对尺寸变大，但是分辨率不会增加，图像会变得更模糊。

测试代码如下：

import cv2 as cv

src = cv.imread("./testimg.jpeg")
print(src.shape[:2])
cv.imshow("src", src)
# 向下采样
dst = cv.pyrDown(src)
print(dst.shape[:2])
cv.imshow("dst", dst)

# 再次向下采样
dst1 = cv.pyrDown(dst)
print(dst1.shape[:2])
cv.imshow("dst1", dst1)

cv.waitKey()

运行代码之后，得到三张图片，大小依次减小，分辨率降低。

通过上面运行得到的最小图，在执行向上采样之后，图片会变的模糊，这也说明上采样和下采样是非线性处理，它们是不可逆的有损处理，因此下采样后的图像是无法还原的，即使放大图片也会变模糊（后面学习到拉普拉斯金字塔可以解决该问题）。

# 向上采样
dst2 = cv.pyrUp(dst1)
print(dst2.shape[:2])
cv.imshow("dst2", dst2)

在总结一下上采样和下采样的步骤：

• 上采样：使用 cv2.pyrUp 函数， 先将图像在每个方向放大为原来的两倍，新增的行和列用 0 填充，再使用先前同样的内核与放大后的图像卷积，获得新增像素的近似值;
• 下采样：使用 cv2.pyrDown 函数，先对图像进行高斯内核卷积 ，再将所有偶数行和列去除。

拉普拉斯金字塔（Laplacian Pyramid， LP）

拉普拉斯金字塔主要用于重建图像，由上文我们已经知道在使用高斯金字塔的的时候，上采样和下采样会导致图像细节丢失。

拉普拉斯就是为了在放大图像的时候，可以预测残差，何为残差，即小图像放大的时候，需要插入一些像素值，在上文直接插入的是 0，拉普拉斯金字塔算法可以根据周围像素进行预测，从而实现对图像最大程度的还原。

学习到原理如下：用高斯金字塔的每一层图像，减去其上一层图像上采样并高斯卷积之后的预测图像，得到一系列的差值图像即为 LP 分解图像（其中 LP 即为拉普拉斯金字塔图像）。

关于拉普拉斯还存在一个公式（这是本系列课程第一次书写公式），其中 L 为拉普拉斯金字塔图像，G 为高斯金字塔图像

使用下面的代码进行测试。

import cv2 as cv

src = cv.imread("./testimg.jpeg")
print(src.shape[:2])
cv.imshow("src", src)
# 向下采样一次
dst = cv.pyrDown(src)
print(dst.shape[:2])
cv.imshow("dst", dst)

# 向上采样一次
dst1 = cv.pyrUp(dst)
print(dst1.shape[:2])
cv.imshow("dst1", dst1)

# 计算拉普拉斯金字塔图像
# 原图 - 向上采样一次的图
laplace = cv.subtract(src, dst1)
cv.imshow("laplace", laplace)
cv.waitKey()

运行结果如下，相关的图像已经呈现出来，重点注意最右侧的图片。

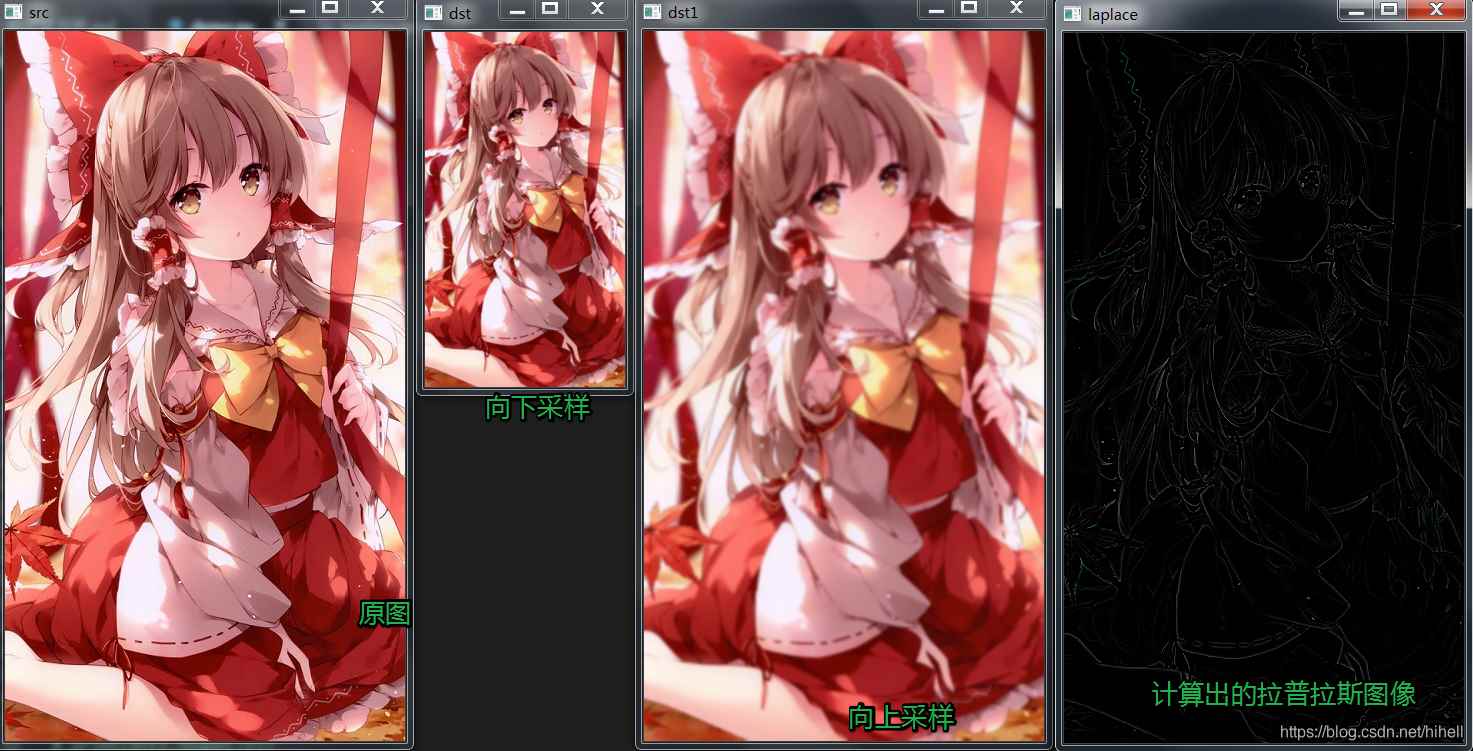
这个地方需要注意下，如果你使用 cv.subtract(src, dst1) 函数，得到的是上图效果，但是在使用还原的时候会发现问题，建议直接使用 -完成，匹配公式，修改代码如下：

# cv.subtract(src, dst1)
laplace = src - dst1

代码运行效果如下。

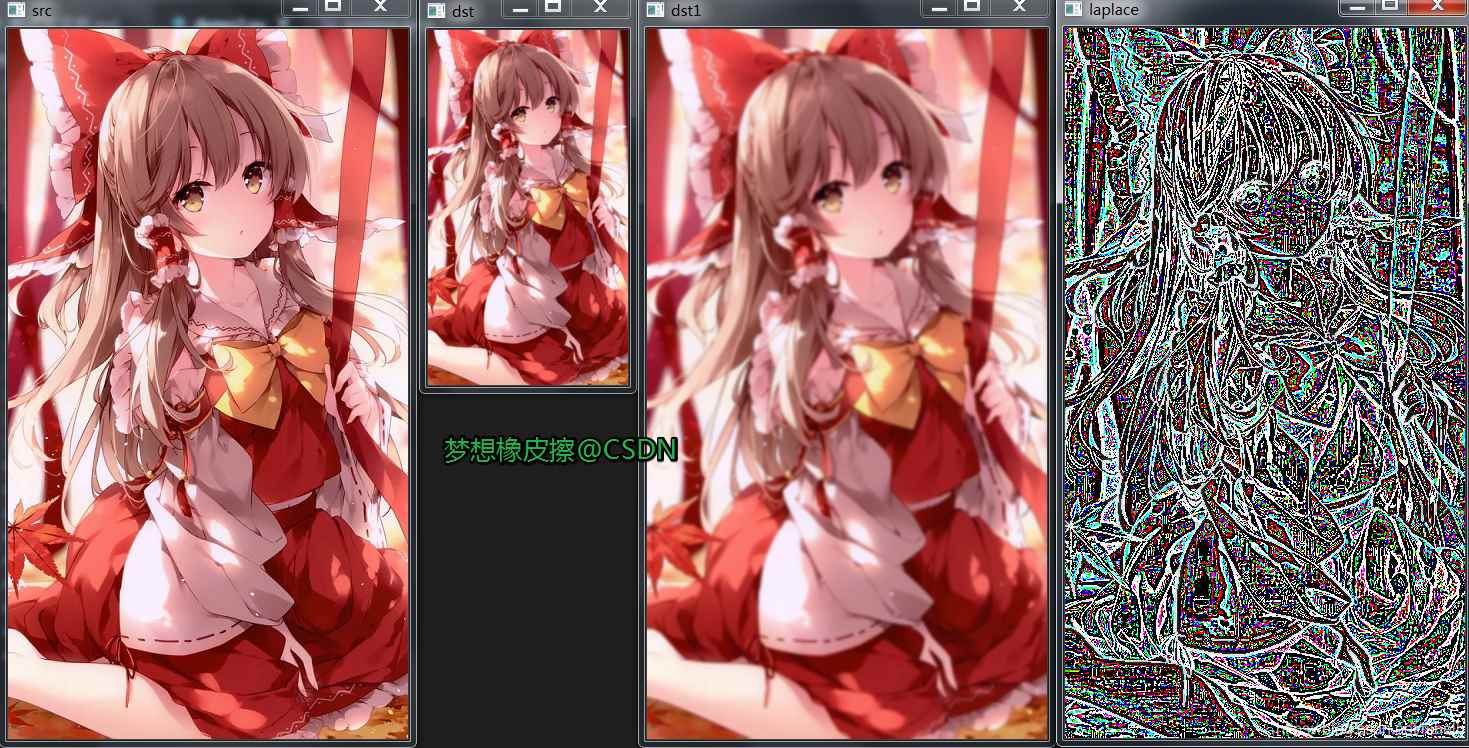
学习过程中发现这样一段话：图像尺寸最好是 2 的整次幂，如 256,512 等，否则在金字塔向上的过程中图像的尺寸会不等，这会导致在拉普拉斯金字塔处理时由于不同尺寸矩阵相减而出错。

这个我在实测的时候发现确实如此，例如案例中使用的图像，在向下采样 2 次的时候，图像的尺寸就会发生变化，测试代码如下：

import cv2 as cv

src = cv.imread("./testimg.jpeg")
print(src.shape[:2])
cv.imshow("src", src)
# 向下采样1次
dst1 = cv.pyrDown(src)
print(dst1.shape[:2])
cv.imshow("dst", dst1)
# 向下采样2次
dst2 = cv.pyrDown(dst1)
print(dst1.shape[:2])
cv.imshow("dst2", dst2)

# 向上采样1次
up_dst1 = cv.pyrUp(dst2)
print(up_dst1.shape[:2])
cv.imshow("up_dst1", up_dst1)

# 计算拉普拉斯金字塔图像
# 采样1次 - 向上采样1次的图
laplace = dst1 - up_dst1
cv.imshow("laplace", laplace)
cv.waitKey()

注意 print(up_dst1.shape[:2]) 部分的输出如下：

(710, 400)
(355, 200)
(355, 200)
(356, 200)

如果在该基础上使用拉普拉斯图像金字塔，就会出现如下错误

Sizes of input arguments do not match

在总结一下拉普拉斯图像金字塔的执行过程：

• 向下采样：用高斯金字塔的第 i 层减去 i+1 层做上采样的图像，得到拉普拉斯第 i 层的图像；
• 向上采样：用高斯金字塔的 i+1 层向上采样加上拉普拉斯的第 i 层，得到第 i 层的原始图像。

向下采样上面的代码已经实现了，但是拉普拉斯向上采样还未实现，完善一下代码如下，为了代码清晰，我们将变量命名进行修改。

import cv2 as cv

src = cv.imread("./testimg_rect.jpeg")
print(src.shape[:2])
cv.imshow("src", src)
# 高斯金字塔第 0 层
gus0 = src # 原图
# 高斯金字塔第 1 层
gus1 = cv.pyrDown(gus0)
# 高斯第 2 层
gus2 = cv.pyrDown(gus1)

# 拉普拉斯金字塔第 0 层
lap0 = gus0 - cv.pyrUp(gus1)
# 拉普拉斯金字塔第 1 层
lap1 = gus1 - cv.pyrUp(gus2)

# 显示拉普拉斯第一层代码
cv.imshow("laplace", lap1)
cv.waitKey()

下面用修改好的代码完成还原图片的操作。

import cv2 as cv

src = cv.imread("./testimg_rect.jpeg")
print(src.shape[:2])
cv.imshow("src", src)
# 高斯金字塔第 0 层
gus0 = src # 原图
# 高斯金字塔第 1 层
gus1 = cv.pyrDown(gus0)
# 高斯第 2 层
gus2 = cv.pyrDown(gus1)

# 拉普拉斯金字塔第 0 层
lap0 = gus0 - cv.pyrUp(gus1)
# 拉普拉斯金字塔第 1 层
lap1 = gus1 - cv.pyrUp(gus2)

rep = lap0 + cv.pyrUp(lap1 + cv.pyrUp(gus2))
gus_rep = cv.pyrUp(cv.pyrUp(gus2))

cv.imshow("rep", rep)
cv.imshow("gus_rep", gus_rep)
cv.waitKey()

以上代码最重要的部分为下面两句：

rep = lap0 + cv.pyrUp(lap1 + cv.pyrUp(gus2))
gus_rep = cv.pyrUp(cv.pyrUp(gus2))

第一行代码中 lap1 + cv.pyrUp(gus2) 即文字公式 【用高斯金字塔的 i+1 层向上采样加上拉普拉斯的第 i 层，得到第 i 层的原始图像】的翻译。

第二行代码是使用直接向上采样，最终得到的是损失细节的图像。

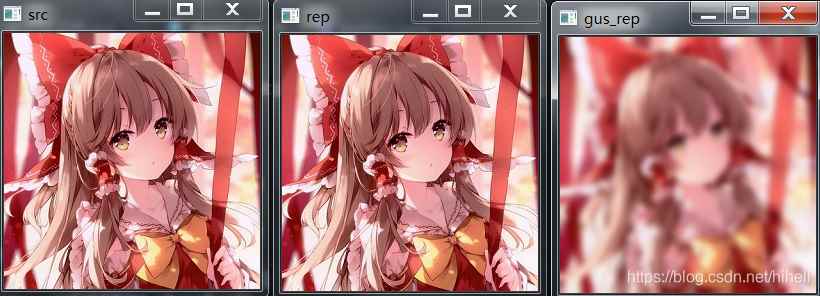
上述代码运行的结果如下，通过拉普拉斯可以完美还原图像。

学习本案例之后，你可以在复盘本文开始部分的代码，将其进行修改。

最后在学习一种技巧，可以直接将两幅图片呈现，代码如下：

import cv2 as cv
import numpy as np
src = cv.imread("./testimg_rect.jpeg")
print(src.shape[:2])
cv.imshow("src", src)
# 向下采样1次
down_dst1 = cv.pyrDown(src)
print(down_dst1.shape[:2])
cv.imshow("dst", down_dst1)

# 向上采样1次
up_dst1 = cv.pyrUp(down_dst1)
print(up_dst1.shape[:2])
cv.imshow("up_dst1", up_dst1)

res = np.hstack((up_dst1, src))
cv.imshow('res', res)

cv.waitKey()

运行之后，通过 np.hstack((up_dst1, src))函数，将两个图像矩阵合并，实现效果如下：

到此这篇关于Python OpenCV高斯金字塔与拉普拉斯金字塔的实现的文章就介绍到这了,更多相关Python OpenCV金字塔内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！