本文实例讲述了Java二叉搜索树基础原理与实现方法。分享给大家供大家参考，具体如下：

前言：本文通过先通过了解一些二叉树基础知识，然后在转向学习二分搜索树。

1 树

1.1 树的定义

树（Tree）是n（n>=0)个节点的有限集。n=0时称为空树。在任意一颗非空树中：

（1）有且仅有一个特定的称为根（Root）的节点；
（2）当n>1时，其余节点可分为m(m>0)个互不相交的有限集T1、T2、......、Tn，其中每一个集合本身又是一棵树，并且称为根的子树。
此外，树的定义还需要强调以下两点：
（3）n>0时根节点是唯一的，不可能存在多个根节点，数据结构中的树只能有一个根节点。
（4）m>0时，子树的个数没有限制，但它们一定是互不相交的。

下图为一棵有10个节点的一般树的结构：

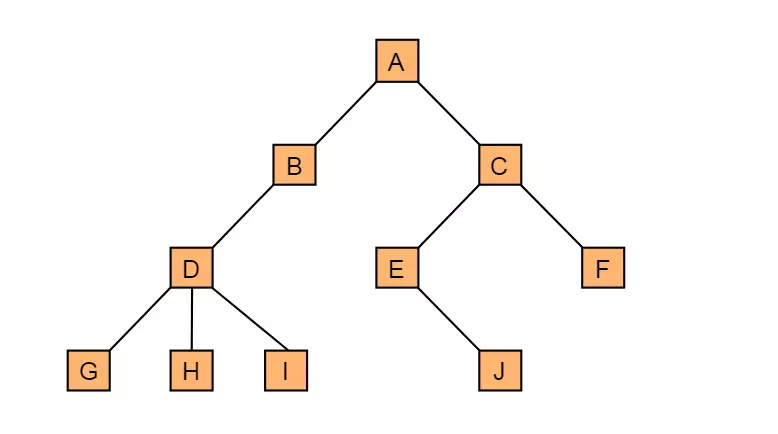
由树的定义可以看出，树的定义使用了递归的方式。递归在树的学习过程中起着重要作用。

2 二叉树

2.1 二叉树定义

二叉树是n(n>=0)个节点的有限集合，该集合或者为空集（称为空二叉树），或者由一个根节点和两棵互不相交的、分别称为根节点的左子树和右子树组成。
图2.1展示了一棵一般二叉树结构：

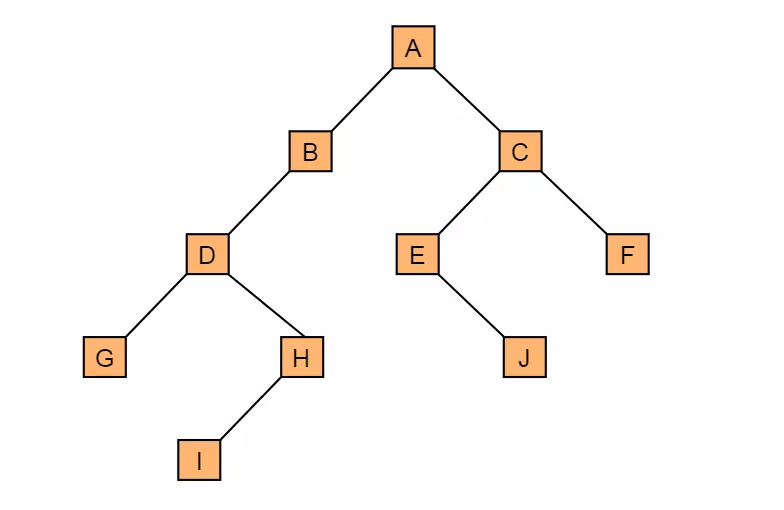
2.2 二叉树特点

由二叉树定义以及图示分析得出二叉树有以下特点:

（1）每个节点最多有两颗子树，所以二叉树中不存在度大于2的节点。
（2）左子树和右子树是有顺序的，次序不能任意颠倒。
（3）即使树中某节点只有一棵子树，也要区分它是左子树还是右子树。
二叉树是动态的数据结构

可以用一下代码来表示一个树节点：

class Node<E>{
  E e;
 Node left;
 Node right;
}

2.2.1 特性

1.二叉树具有天然的递归结构

这是由于，每个节点的左子树与右子树都是二叉树（有的情况下），如图：

2.2.2 二分树类型（展示）
类型1：

类型2：

类型3：

类型4：

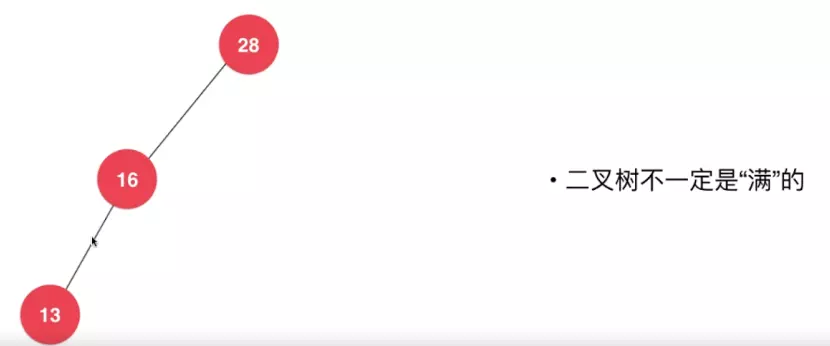
类型5：

3.二叉搜索树

3.1 定义

二叉查找树（Binary Search Tree），也称有序二叉树（ordered binary tree）、排序二叉树（sorted binary tree），是指一棵空树或者具有下列性质的二叉树：

1.若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
2.任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
3.任意节点的左、右子树也分别为二叉查找树。
4.没有键值相等的节点（no duplicate nodes）。

因此使用二叉树存储的元素必须有可比性。

3.2二叉搜索树的性质：

二叉查找树本质上是一种二叉树，所以上章讲的二叉树的性质他都有。

3.3二分搜索树的思想：

二叉排序树的查找过程和次优二叉树类似，通常采取二叉链表作为二叉排序树的存储结构。中序遍历二叉排序树可得到一个关键字的有序序列，一个无序序列可以通过构造一棵二叉排序树变成一个有序序列，构造树的过程即为对无序序列进行排序的过程。每次插入的新的结点都是二叉排序树上新的叶子结点，在进行插入操作时，不必移动其它结点，只需改动某个结点的指针，由空变为非空即可。搜索,插入,删除的复杂度等于树高，O(log(n)),后续逐一进行学习。

4.编程实现二叉搜索树

4.1 基础代码

由于使用二叉树存储的元素必须有可比性，因此在实现时需要BST类继承Comparable。

package BST;

public class BST<E extends Comparable<E>> {

  //定义树节点
  private class Node {
    public E e;
    public Node left, right;

    public Node(E e) {
      this.e = e;
      left = null;
      right = null;
    }
  }

  private Node root;//根节点
  private int size;

  public BST() {
    root = null;
    size = 0;
  }

  //二分搜索树存储元素个数
  public int size() {
    return size;
  }

  //二分搜索树存储元素是否为空
  public boolean isEmpty() {
    return size == 0;
  }
}

本节算是二叉搜索树的一个入门，后续将继续完善、更新。

更多关于java算法相关内容感兴趣的读者可查看本站专题：《Java数据结构与算法教程》、《Java操作DOM节点技巧总结》、《Java文件与目录操作技巧汇总》和《Java缓存操作技巧汇总》

希望本文所述对大家java程序设计有所帮助。