二叉树的概念案例详解

二叉树简介

关于树的介绍，请参考：https://blog.csdn.net/weixin_43790276/article/details/104033482

一、二叉树简介

二叉树是每个节点最多有两个子树的树结构，是一种特殊的树，如下图，就是一棵二叉树。

二叉树是由n(n>=0)个节点组成的数据集合。当 n=0 时，二叉树中没有节点，称为空二叉树。当 n=1 时，二叉树只有根节点一个节点。当 n>1 时，二叉树的每个节点都最多只能有两个子树，递归地构建成一棵完整的二叉树。

二叉树的两个子树被称为左子树(left subtree)和右子树(right subtree)。在二叉树中，如果节点没有子树，则左子树和右子树都为空，如果节点只有一个子树，要根据子树的左右来区分子树是左子树还是右子树，如果节点有两个子树，则左子树和右子树都有。

如果，树中存在一个节点，该节点的子树超过两个，则该树不是二叉树，如下图中，节点C有三个子树，所以这不是一棵二叉树。

二、几种特殊的二叉树

只要树中所有节点的子树都不超过两个(0个，1个，2个)，这就是一棵普通的二叉树。在二叉树中，有一些比较特殊，除了满足二叉树的结构外，还满足一些特殊的规则，主要有如下几种。

1. 完全二叉树：假设一棵二叉树的深度为d(d>1)，除了第d层外，其它各层的节点数目均已达最大值，且第d层所有节点从左向右连续地紧密排列，这样的二叉树被称为完全二叉树。

完全二叉树的叶节点只能出现在最下层和次下层，最下层的叶节点靠左紧密地排列，次下层如果存在叶节点，叶节点紧密地靠右排列。

如下图，树的深度为4，除了第4层，节点数达到了最大(“挂满了”)，第4层的节点都是紧密地靠左排列(中间没有空位)，所以这是一棵完全二叉树。

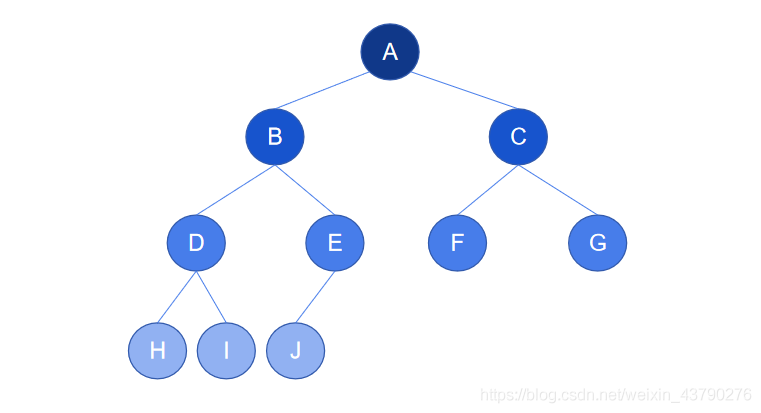
如下图，树的深度也为4，除了第4层，节点数也达到了最大，但是第4层的节点不是紧靠左侧排列的(节点E没有子节点，空了两个位置)，所以这不是一棵完全二叉树，只是一棵普通的二叉树。

2. 满二叉树：所有叶节点都在最底层的完全二叉树称为满二叉树。满二叉树是完全二叉树中的特殊情况，除了满足完全二叉树的特征，还满足所有叶节点都在最底层。满二叉树是相同深度的二叉树中叶节点最多的树。

如下图，这首先是一棵完全二叉树，其次，所有的叶节点都在最底层，所以这是一棵满二叉树。其实，满二叉树也可以这么定义，二叉树有节点的所有层，节点数目均已达最大值，则这是一棵满二叉树。

3. 平衡二叉树(AVL树)：如果二叉树的所有节点的两棵子树的高度差不大于1，则二叉树被称为平衡二叉树。

如上图中的满二叉树，任何节点的两棵子树高度差都是0(高度都相等，高度差不大于1)，所以这是一棵平衡二叉树。

如下图中的二叉树，对于根节点A，左子树是以节点B为根的子树，高度为4，右子树是以节点C为根的子树，高为2，A的左子树与右子树的高度差为2(高度差大于1)，所以这不是一棵平衡二叉树。

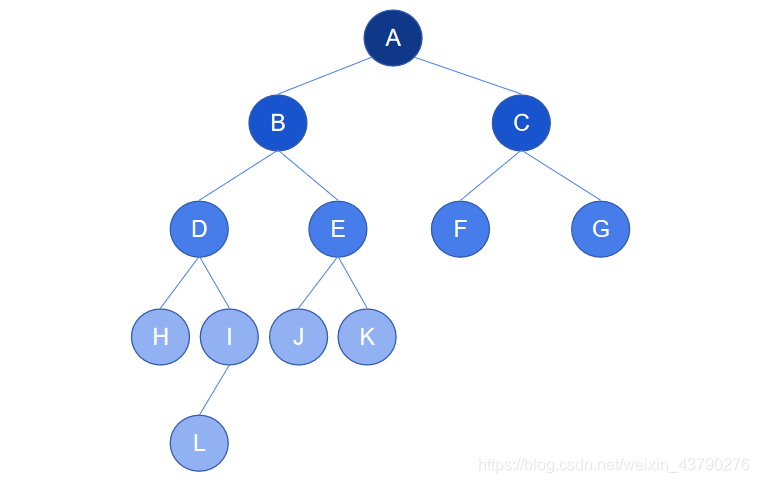
AVL树得名于它的发明者G. M. Adelson-Velsky和E. M. Landis，是两人姓的缩写。AVL树中任何节点的两个子树的高度差不大于1，通过高度来判断是否平衡，所以也被称为高度平衡树。

4. 排序二叉树(二叉查找树，Binary Search Tree)：又称为二叉搜索树、有序二叉树。

排序二叉树需要具有如下的性质：

4.1 如果二叉树的左子树不为空，则左子树上所有节点的值均小于它的根节点的值。

4.2 如果二叉树的右子树不为空，则右子树上所有节点的值均大于它的根节点的值。

4.3 如果独立地看，左子树、右子树也分别为排序二叉树，用递归的思想，直到树的叶节点。

如下图，根节点8的左子树中，所有节点的值都小于根节点，右子树中，所有节点的值都大于根节点，并且左子树和右子树都是排序二叉树，所以这是一棵排序二叉树。

5. 斜树：除了叶节点，所有节点都只有左子树的二叉树称为左斜树。除了叶节点，所有节点都只有右子树的二叉树称为右斜树。他们统称为斜树，判断二叉树是否为斜树，主要是看树的结构，对节点的值没有要求。

如下图，左边的树中，除了叶节点D，所有节点都只有左子树，这是一棵左斜树，同理，右边的树是一棵右斜树。

三、二叉树的特点和性质

通过对二叉树的介绍和对几种特殊二叉树的了解，可知二叉树有以下特点：

1. 每个节点最多有两颗子树，所以二叉树中节点的度不大于2，二叉树的度也不会大于2。

2. 左子树和右子树的次序不能颠倒。

3. 即使某节点只有一棵子树，也要根据左右来区分它是左子树还是右子树。

此外，二叉树还具有如下性质：

1. 在二叉树的第i层，至多有 2^(i-1) 个节点(i>0) 。

这里说的是至多的情况，满二叉树的每一层节点都“挂满”了，所以可以用下图中的满二叉树来验证，第1层的节点数为2^(1-1)=1个，... 第4层的节点个数最多为 2^(4-1)=8个。

2. 深度为i的二叉树至多有 2^i - 1 个节点(k>0) 。

这里也是说至多的情况，所以也用满二叉树来验证，深度为4时，二叉树的节点数最多为 2^4 - 1=16-1=15个。

3. 对于任意一棵二叉树，如果其叶节点数为M，度为2的节点总数为N，则 M=N+1 。

为了不失一般性，下图中的树是一棵普通的二叉树，叶节点为 F,H,I,J,K,L ，共6个，度为2的节点为 A,B,C,D,G ，共5个。

4. 具有n个节点的满二叉树的深度必为 log2(n+1) 。这个性质是上面第2点的逆运算。

5. 对于一棵完全二叉树，若从上至下、从左至右编号，则编号为 i 的节点，(叶节点除外)其左子节点的编号必为2i，(叶节点除外)其右子节点的编号必为 2i+1，(根节点除外)其父节点的编号必为i/2(取整除)。

如下图，这是一棵完全二叉树，已经按规则编好号了，可以任意取一个节点进行验证，都是符合此性质的。

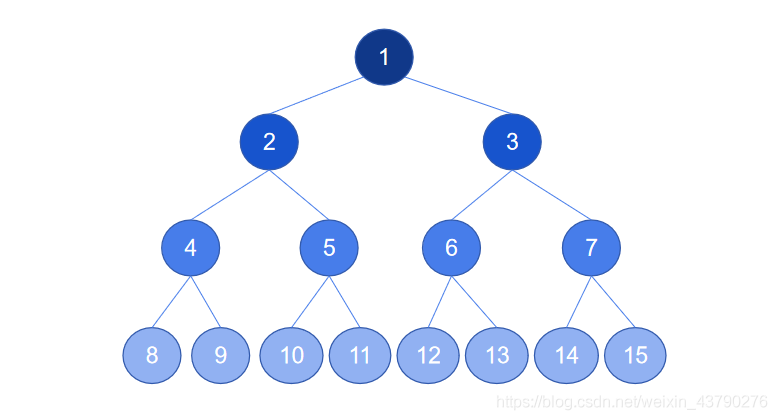
到此这篇关于二叉树的概念案例详解的文章就介绍到这了,更多相关二叉树的概念内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！