java版十大排序经典算法:完整代码

目录

• 十大排序算法对比
• 冒泡排序
• 完整代码：
• 测试代码：
• 运行结果：
• 快速排序
• 完整代码：
• 总结

十大排序算法对比

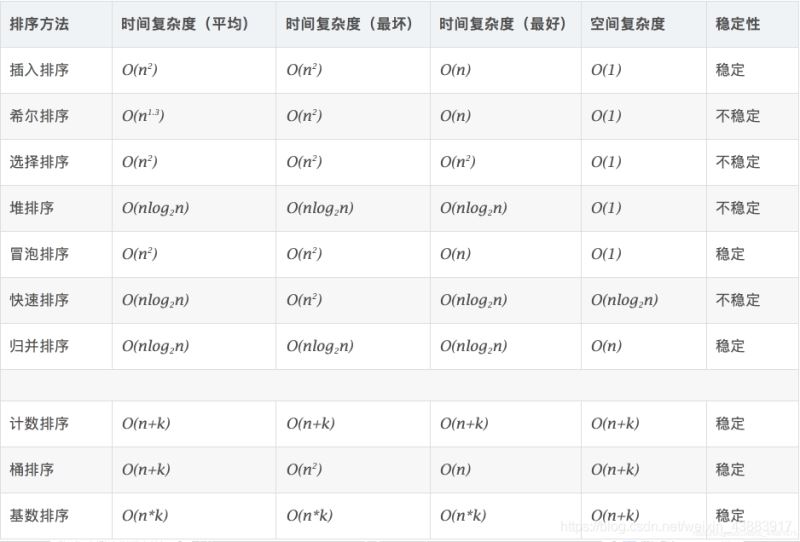
关于最后一列的稳定性，我稍微解释下，例如对序列：1 2 4 2 6 排序，序列中存在两个2，如果我们把这两个2标记上（让他俩不同），排序之后，前面的2还在前面，那么就称这种排序是稳定的，反之不稳定。

冒泡排序

简单解释： 原理就如算法名字一样，就像水中的气泡一样，每次我都把最大的或最小的放到最后面，这样总共需要n-1趟即可完成排序，这就是第一层循环，第二次循环就是遍历未被固定的那些数（理解成数组左边的数，因为每层循环都会把最大或最小的数升到最右边固定起来，下次就不遍历这些数了），两层循环遍历结束后，所有的数就排好序了。 两层循环所以冒泡排序算法的时间复杂度是O( n 2 n^{2} n2)，是一个非常高的时间复杂度，我在下面的代码进行了优化，加了一个标志位，如果上一次循环未发生交换，就说明已经是有序的了，就不继续下去了，反之继续进行下一轮。

完整代码：

package com.keafmd.Sequence;
/**
 * Keafmd
 *
 * @ClassName: BubbleSort
 * @Description: 冒泡排序
 * @author: 牛哄哄的柯南
 * @date: 2021-06-24 10:31
 */
public class BubbleSort {
    //冒泡排序
    public static void bubbleSort(int[] arr, boolean ascending) { //exchange标志表示为升序排序还是降序排序
        boolean flag = true; //加一个标志位，记录上一次是否发生了交换，如果是，我们则进行下一轮，如果没有，说明已经冒泡好了
        for (int i = 1; i < arr.length && flag; i++) { //控制次数，第几趟排序，只需要n-1趟，有交换时进行，只有flag=false就说明上一次一个元素都没有进行交换
            /*System.out.print("第"+i+"次遍历：");
            for (int i1 : arr) {
                System.out.print(i1+" ");
            }
            System.out.println();*/
            flag = false; //假定未交换
            for (int j = 0; j < arr.length - i; j++) {
                if (ascending ? arr[j] > arr[j + 1] : arr[j] < arr[j + 1]) { //控制升序还是降序
                    int temp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;
                    flag = true;
                }
            }
        }
    }
    //冒泡排序 -- 默认不传参升序
    public static void bubbleSort(int[] arr) {
        bubbleSort(arr, true);
    }
}

测试代码：

升序排序（从小到大）

package com.keafmd.Sequence;
import java.util.*;
import java.util.stream.IntStream;
import java.util.stream.Stream;
/**
 * Keafmd
 *
 * @ClassName: Sort
 * @Description: 十大排序算法
 * @author: 牛哄哄的柯南
 * @date: 2021-06-16 21:27
 */
public class Sort {
    public static void main(String[] args) {
        int[] nums = {12, 4, 25, 47, 58, 34, 25, 9, 99, 26, 1, -13, 162, 10093, -66, -1};
        int[] temparr;
        //测试冒泡排序
        System.out.println("测试冒泡排序:");
        temparr = nums.clone();
        BubbleSort.bubbleSort(temparr);
        //逆序排序
        //BubbleSort.bubbleSort(temparr,false);
        for (int i = 0; i < temparr.length; i++) {
            System.out.print(temparr[i] + " ");
        }
        System.out.println();
    }
}

运行结果：

测试冒泡排序: -66 -13 -1 1 4 9 12 25 25 26 34 47 58 99 162 10093

降序排序（从大到小）

//测试冒泡排序
System.out.println("测试冒泡排序:");
temparr = nums.clone();
BubbleSort.bubbleSort(temparr,false);
for (int i = 0; i < temparr.length; i++) {
    System.out.print(temparr[i] + " ");
}
System.out.println();

运行结果：

测试冒泡排序: 10093 162 99 58 47 34 26 25 25 12 9 4 1 -1 -13 -66

下面几个算法的测试也就是换了下类名和方法名（换成相应的排序算法），如果想降序就在数组后面传个false即可。我就不一一复制了，我在最下面给出含所有算法的测试类，需要的自取即可。

快速排序

简单解释：快速排序就是每次找一个基点（第一个元素），然后两个哨兵，一个从最前面往后走，一个从最后面往前面走，如果后面那个哨兵找到了一个比基点大的数停下来，前面那个哨兵找到比基点大的数停下来，然后交换两个哨兵找到的数，如果找不到最后两个哨兵就会碰到一起就结束，最后交换基点和哨兵相遇的地方的元素，然后就将一个序列分为比基点小的一部分和比基点大的一部分，然后递归左半部分和右半部分，最后的结果就是有序的了。

完整代码：

package com.keafmd.Sequence;
/**
 * Keafmd
 *
 * @ClassName: QuickSort
 * @Description: 快速排序
 * @author: 牛哄哄的柯南
 * @date: 2021-06-24 10:32
 */
public class QuickSort {
    //快速排序
    public static void quickSort(int[] arr) {
        quickSort(arr, true);
    }
    public static void quickSort(int[] arr, boolean ascending) {
        if (ascending) {
            quickSort(arr, 0, arr.length - 1, true);
        } else {
            quickSort(arr, 0, arr.length - 1, false);
        }
    }
    public static void quickSort(int[] arr, int begin, int end, boolean ascending) {
        if (ascending)
            quickSort(arr, begin, end);
        else
            quickSortDescending(arr, begin, end);
    }
    //快排序升序 -- 默认
    public static void quickSort(int[] arr, int begin, int end) {
        if (begin > end) { //结束条件
            return;
        }
        int base = arr[begin];
        int i = begin, j = end;
        while (i < j) { // 两个哨兵（i左边，j右边）没有相遇
            while (arr[j] >= base && i < j) { //哨兵j没找到比base小的
                j--;
            }
            while (arr[i] <= base && i < j) { //哨兵i没找到比base大的
                i++;
            }
            if (i < j) { //如果满足条件则交换
                int temp = arr[i];
                arr[i] = arr[j];
                arr[j] = temp;
            }
        }
        //最后将基准为与i和j相等位置的数字交换
        arr[begin] = arr[i];
        arr[i] = base;
        quickSort(arr, begin, i - 1); //递归调用左半数组
        quickSort(arr, i + 1, end); //递归调用右半数组
    }
    //快排序降序
    public static void quickSortDescending(int[] arr, int begin, int end) {
        if (begin > end) { //结束条件
            return;
        }
        int base = arr[begin];
        int i = begin, j = end;
        while (i < j) { // 两个哨兵（i左边，j右边）没有相遇
            while (arr[j] <= base && i < j) { //哨兵j没找到比base大的
                j--;
            }
            while (arr[i] >= base && i < j) { //哨兵i没找到比base小的
                i++;
            }
            if (i < j) { //如果满足条件则交换
                int temp = arr[i];
                arr[i] = arr[j];
                arr[j] = temp;
            }
        }
        //最后将基准为与i和j相等位置的数字交换
        arr[begin] = arr[i];
        arr[i] = base;
        quickSortDescending(arr, begin, i - 1); //递归调用左半数组
        quickSortDescending(arr, i + 1, end); //递归调用右半数组
    }
}

总结

本篇文章就到这里了，希望能给你带来帮助，也希望您能够多多关注我们的更多内容！