Java数据结构之AC自动机算法的实现

目录

• 1 概念和原理
• 2 节点定义
• 3 构建Trie前缀树
• 4 构建fail失配指针
• 5 匹配文本
• 6 案例演示
• 7 总结

1 概念和原理

一般的字符串匹配算法都是匹配一个子串，例如KMP、Trie，那么如果同时匹配多个子串呢？此时就需要用到AC自动机了。

AC自动机算法是一个多模式字符串匹配算法，在模式匹配领域被广泛应用，例如违禁词查找替换、搜索关键词查找等等。

关于Trie树和KMP算法，我们此前已经讲解过了：

• 前缀树Trie的实现原理以及Java代码的实现
• KMP算法详解以及Java代码实现

AC自动机算法常被认为是Trie树+KMP算法的结合体，为什么呢？我们先看看它的构建步骤：

• 对所有的关键词构建Trie前缀树。
• 为Trie树上的所有节点构建fail失配指针。

第一步，对所有的关键词构建Trie前缀树。这一步利用Trie的特点构建快速前缀查找结构，trie树的特点是可以从字符串头部开始匹配，并且相同前缀的词共用前面的节点，因此它可以避免相同前缀pattern的重复匹配，但是对于相同的后缀无能为力。

第二步，为Trie树上的所有节点构建fail失配指针，即匹配失败后应该跳到哪个节点。所谓节点的失配指针，就是指向当前字符串最长真后缀位置的指针节点。这里需要理解KMP的next数组的概念，这一步就是利用KMP前后缀匹配的思想实现关键词前缀失配时利用相同的后缀信息快速跳转到另一个关键词继续前缀匹配。他们的区别是：

• 在KMP算法中，是针对单个关键词匹配，求出的最长匹配长度的前缀和后缀都位于同一个关键词内。例如关键词abcdabc，最长匹配前后缀，为abc，他们属于该关键词。
• 在AC自动机算法中，是针对多个关键词匹配，求出的最长匹配长度的前缀和后缀分别属于不同的关键词的前缀和后缀。

例如两个关键词dabab，ababd，那么关键词dabab中第二个b位置的失败指针应该指向关键词ababd中的第二个b。即dabab的后缀与ababd的前缀能够匹配的最长子串为abab。

2 节点定义

在这里，我们给出一个比较简单的节点的定义。

• next，表示经过该节点的模式串的下层节点，这是Trie树结构的保证，存储着子节点的值到对应的节点的映射关系。
• depth，表示以当前即诶单结尾的模式串的长度，也是节点的深度，默认为0。
• failure，失配指针，其指向表示另一个关键词前缀的最长后缀节点，如果当前节点没有匹配到，则跳转到此节点继续匹配。如果当前节点匹配到了，那么可以通过此指针找到该节点的模式串包含的最长后缀模式串。

class AcNode {
    /**
     * 经过该节点的模式串的下层节点
     */
    Map<Character, AcNode> next = new HashMap<>();

    /**
     * 模式串的长度，也是节点的深度
     */
    int depth;

    /**
     * 失配指针，如果没有匹配到，则跳转到此状态。
     */
    AcNode failure;

    public boolean hashNext(char nextKey) {
        return next.containsKey(nextKey);
    }

    public AcNode getNext(char nextKey) {
        return next.get(nextKey);
    }
}

3 构建Trie前缀树

构建Ac自动机的Trie的方法和构建普通Trie的方法几乎一致。在添加每个模式串成功后，会为最后一个节点的depth赋值为当前模式串的长度。

/**
 * trie根节点
 */
private AcNode root;
/**
 * 加入模式串，构建Trie
 *
 * @param word 模式串，非空
 */
public void insert(String word) {
    AcNode cur = root;
    for (char c : word.toCharArray()) {
        if (!cur.next.containsKey(c)) {
            cur.next.put(c, new AcNode());
        }
        cur = cur.next.get(c);
    }
    cur.depth = word.length();
}

4 构建fail失配指针

构建fail失配指针的一种常见的方法如下，实际上是一个BFS层序遍历的算法：

1.Trie的root节点没有失配指针，或者说失配指针为null，其他节点都有失配指针，或者说不为null。

2.遍历root节点的所有下一层直接子节点，将它们的失配指针设置为root。因为这些节点代表着所有模式串的第一个字符，基于KMP的next数组定义，单个字符没有最长真后缀，此时直接指向root。

3.继续循环向下遍历每一层的子节点，由于bfs的遍历，那么上一层父节点的失配指针肯定都已经确定了。基于next数组的构建思想，子节点的失配指针可以通过父节点的是失配指针快速推导出来。设当前遍历的节点为c，它的父节点为p，父节点的失配指针为pf。

• 如果pf节点的子节点对应的字符中，包含了当前节点的所表示的字符。那么基于求最长后缀的原理，此时c节点的失配指针可以直接指向pf节点下的相同字符对应的子节点。
• 如果pf节点的子节点对应的字符中，没有包含了当前节点的所表示的字符。那么继续获取pf节点的失配指针节点，继续重复判断。直到满足第一种情况，或者pf指向了根节点，并且根节点的子节点也没有匹配，那么此时直接将c节点的失配指针指向根节点。

/**
 * 为所有节点构建失配指针，一个bfs层序遍历
 */
public void buildFailurePointer() {
    ArrayDeque<AcNode> queue = new ArrayDeque<AcNode>();
    //将所有root的直接子节点的failure设置为root，并且加入queue
    for (AcNode acNode : root.next.values()) {
        acNode.failure = root;
        queue.addLast(acNode);
    }
    //bfs构建失配指针
    while (!queue.isEmpty()) {
        //父节点出队列
        AcNode parent = queue.pollFirst();
        //遍历父节点的下层子节点，基于父节点求子节点的失配指针
        for (Map.Entry<Character, AcNode> characterAcNodeEntry : parent.next.entrySet()) {
            //获取父节点的失配指针
            AcNode pf = parent.failure;
            //获取子节点
            AcNode child = characterAcNodeEntry.getValue();
            //获取子节点对应的字符
            Character nextKey = characterAcNodeEntry.getKey();
            //如果pf节点不为null，并且pf节点的子节点对应的字符中，没有包含了当前节点的所表示的字符
            while (pf != null && !pf.hashNext(nextKey)) {
                //继续获取pf节点的失配指针节点，继续重复判断
                pf = pf.failure;
            }
            //pf为null，表示找到了根节点，并且根节点的子节点也没有匹配
            if (pf == null) {
                //此时直接将节点的失配指针指向根节点
                child.failure = root;
            }
            //pf节点的子节点对应的字符中，包含了当前节点的所表示的字符
            else {
                //节点的失配指针可以直接指向pf节点下的相同字符对应的子节点
                child.failure = pf.getNext(nextKey);
            }
            //最后不要忘了，将当前节点加入队列
            queue.addLast(child);
        }
    }
}

5 匹配文本

构建完AC自动机之后，下面我们需要进行文本的匹配，匹配的方式实际上比较简单。

1.遍历文本的每个字符，依次匹配，从Trie的根节点作为cur节点开始匹配：

2.将当前字符作为nextKey，如果cur节点不为null且节点的next映射中不包含nextKey，那么当前cur节点指向自己的failure失配指针。

3.如果cur节点为null，说明当前字符匹配到了root根节点且失败，那么cur设置为root继续从根节点开始进行下一轮匹配。

4.否则表示匹配成功的节点，cur指向匹配节点，获取该节点继续判断：

• 如果该节点是某个关键词的结尾，那么取出来，也就是depth不为0，那么表示匹配到了一个关键词。
• 继续判断该节点的失配指针节点表示的模式串。因为失配指针节点表示的模式串是当前匹配的模式串的在这些关键词中的最长后缀，且由于当前节点的路径包括了失配指针的全部路径，并且失配指针路径也是一个完整的关键词，需要找出来。

/**
 * 匹配文本
 *
 * @param text 文本字符串
 */
public List<ParseResult> parseText(String text) {
    List<ParseResult> parseResults = new ArrayList<>();
    char[] chars = text.toCharArray();
    //从根节点开始匹配
    AcNode cur = root;
    //遍历字符串的每个字符
    for (int i = 0; i < chars.length; i++) {
        //当前字符
        char nextKey = chars[i];
        //如果cur不为null，并且当前节点的的子节点不包括当前字符，即不匹配
        while (cur != null && !cur.hashNext(nextKey)) {
            //那么通过失配指针转移到下一个节点继续匹配
            cur = cur.failure;
        }
        //如果节点为null，说明当前字符匹配到了根节点且失败
        //那么继续从根节点开始进行下一轮匹配
        if (cur == null) {
            cur = root;
        } else {
            //匹配成功的节点
            cur = cur.getNext(nextKey);
            //继续判断
            AcNode temp = cur;
            while (temp != null) {
                //如果当前节点是某个关键词的结尾，那么取出来
                if (temp.depth != 0) {
                    int start = i - temp.depth + 1, end = i;
                    parseResults.add(new ParseResult(start, end, new String(chars, start, temp.depth)));
                    //System.out.println(start + " " + end + " " + new String(chars, start, temp.depth));
                }
                //继续判断该节点的失配指针节点
                //因为失配指针节点表示的模式串是当前匹配的模式串的在这些关键词中的最长后缀，且由于当前节点的路径包括了失配指针的全部路径
                //并且失配指针路径也是一个完整的关键词，需要找出来。
                temp = temp.failure;
            }
        }
    }
    return parseResults;
}

class ParseResult {
    int startIndex;
    int endIndex;
    String key;

    public ParseResult(int startIndex, int endIndex, String key) {
        this.startIndex = startIndex;
        this.endIndex = endIndex;
        this.key = key;
    }

    @Override
    public String toString() {
        return "{" +
                "startIndex=" + startIndex +
                ", endIndex=" + endIndex +
                ", key='" + key + '\'' +
                '}';
    }
}

6 案例演示

基于上面的方法，假如关键词为：he、shes、shers、hes、h、e，那么最终构建的AC自动机的结构如下（红色圈表示某个关键词的结束位置）。

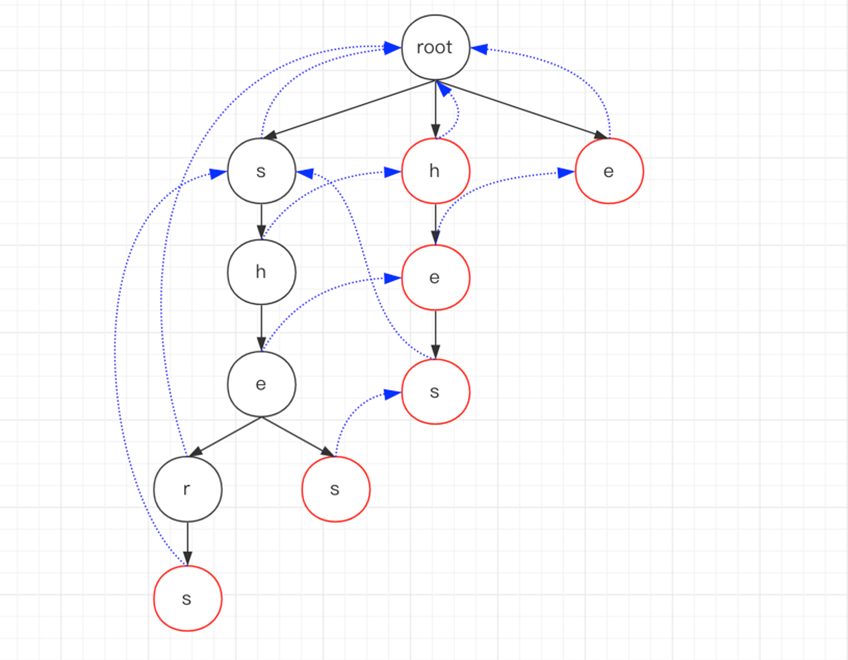
假如我们的文本为sheshe，那么我们来看看AC自动机匹配的过程：

遍历文本，cur首先指向root。

nextKey=s，cur.next包含s，表示这是一个匹配成功的节点，那么获取到该节点s，cur=s，s不是某个关键词的结尾，failure节点也不包含模式串，那么查找完毕进行下一轮。

nextKey=h，cur=s，cur.next包含h，表示这是一个匹配成功的节点，那么获取到该节点h，cur=h，h节点不是某个关键词的结尾，但是它的failure节点包含模式串h，因此找到了第1个匹配的关键词h，查找完毕后进行下一轮。

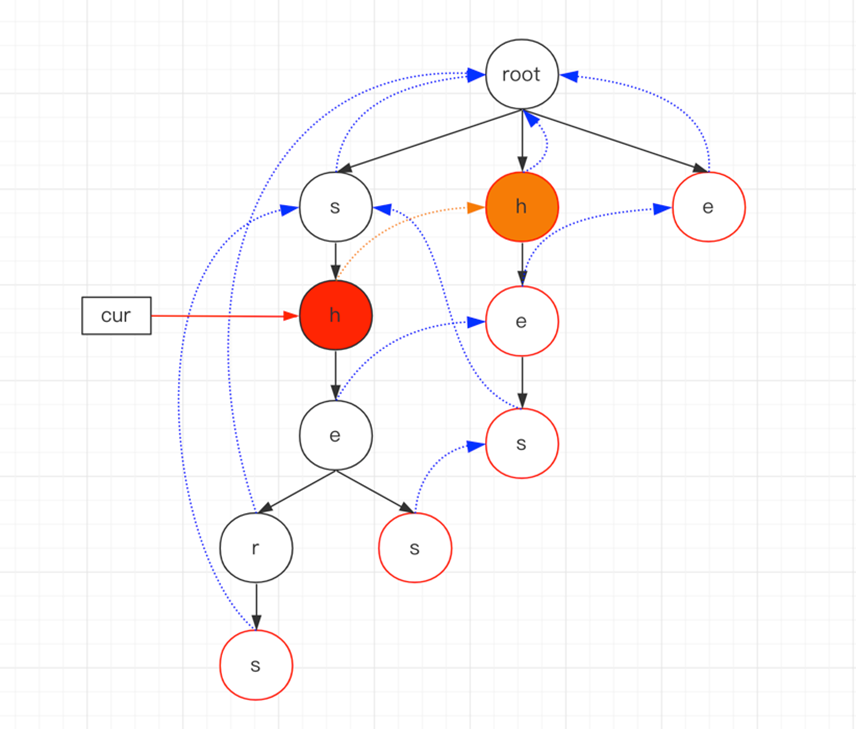
nextKey=e，cur=h，cur.next包含e，表示这是一个匹配成功的节点，那么获取到该节点e，cur=e，e节点不是某个关键词的结尾，但是它的failure节点包含模式串he，因此找到了第2个匹配的关键词he。

而fuilure节点e又包含另一个模式串e，因此找到了第3个匹配的关键词e，查找完毕后进行下一轮。

nextKey=s，cur=e，cur.next包含s，表示这是一个匹配成功的节点，那么获取到该节点e，cur=e，s节点是关键词shes的结尾，因此找到了第4个匹配的关键词shes。

继续判断s的failure，它的failure节点包含模式串hes，因此找到了第5个匹配的关键词hes，查找完毕后进行下一轮。

nextKey=h，cur=s，cur.next不包含h，表示这是一个匹配失败的节点，那么继续匹配它的failure节点，经过s-s-s的匹配，最终匹配到子节点h。

该节点h并不是关键词的结尾，但是h的failure，它的failure节点包含模式串h，因此找到了第6个匹配的关键词h，查找完毕后进行下一轮。

nextKey=e，cur=h，cur.next包含e，表示这是一个匹配成功的节点，那么获取到该节点e，cur=e，e节点不是某个关键词的结尾，但是它的failure节点包含模式串he，因此找到了第7个匹配的关键词he。

而fuilure节点e又包含另一个模式串e，因此找到了第8个匹配的关键词e。

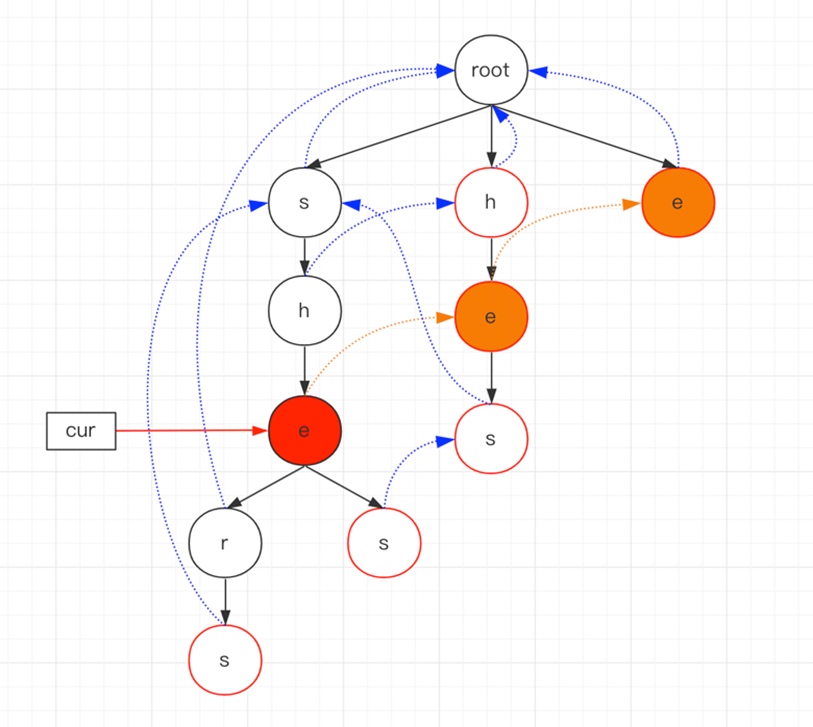
到此字符串遍历完毕，查找完毕！

最终文本sheshe，匹配到关键词如下：

[{startIndex=1, endIndex=1, key='h'}, {startIndex=1, endIndex=2, key='he'}, 
{startIndex=2, endIndex=2, key='e'}, {startIndex=0, endIndex=3, key='shes'}, 
{startIndex=1, endIndex=3, key='hes'}, {startIndex=4, endIndex=4, key='h'}, 
{startIndex=4, endIndex=5, key='he'}, {startIndex=5, endIndex=5, key='e'}]

7 总结

AC自动机匹配某个文本text，需要遍历文本的每个字符，每次遍历过程中，都可能涉及到循环向上查找失配指针的情况，但是这里的循环次数不会超过Trie树的深度，在最后匹配成功时，同样涉及到向上查找失配指针的情况，这里的循环次数不会超过Trie树的深度。

设匹配的文本长度m，模式串平均长度n，那么AC自动机算法的匹配的时间复杂度为O(m*n)。可以发现，匹配的时间复杂度和关键词的数量无关，这就是AC自动机的强大之处。如果考虑模式串平均长度不会很长，那么时间复杂度近似O(m)。

到此这篇关于Java数据结构之AC自动机算法的实现的文章就介绍到这了,更多相关Java AC自动机算法内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！