数据结构 红黑树的详解

数据结构 红黑树的详解

红黑树是具有下列着色性质的二叉查找树：

1.每一个节点或者着红色，或者着黑色。

2.根是黑色的。

3.如果一个节点是红色的，那么它的子节点必须是黑色。

4.从一个节点到一个NULL指针的每一条路径必须包含相同数目的黑色节点。

下面是一棵红黑树。

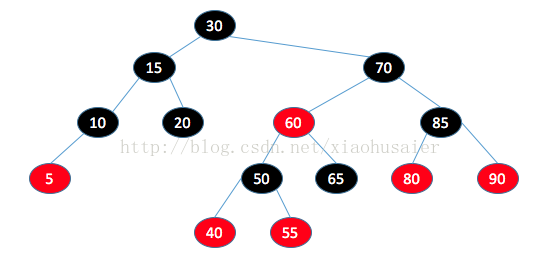
1.自底向上插入

通常把新项作为树叶放到树中。如果我们把该项涂成黑色，那么违反条件4，因为将会建立一条更长的黑节点路径。因此这一项必须涂成红色。如果它的父节点是黑色的，插入完成。如果父节点是红色的，那么违反条件3。在这种情况下我们必须调整该树以满足条件3。用于完成这项目任务的基本操作是颜色的改变和树的旋转。

如果新插入的节点的父节点是黑色，那么插入完成。

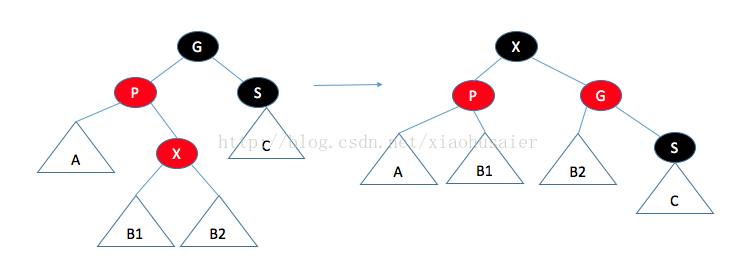
如果父节点是红色，那么有几种情形需要考虑。首先，假设这个父节点的兄弟是黑色（NULL节点约定为黑色）。这对于插入3或8是适用的，但对插入99不适用。令X是新加的树叶，P是它的父节点，S是该父节点的兄弟，G是祖父节点情况一：父节点的兄弟是黑色的。通过操作使得到达A,B,C的黑色路径保持不变（满足条件4），而且没有连续的红色节点（满足条件3）.。

情况二：父节点的兄弟是红色的。

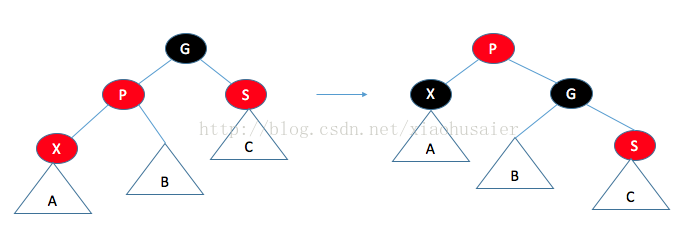
2.自顶向下删除

红黑树中的删除可以是自顶向下进行。每一件工作都归结于能够删除一片树叶。这是因为，要删除一个带有两个儿子的节点，我们用右子树上的最小节点代替它；该节点最多有一个儿子，然后将该节点删除。只有一个右儿子的节点可以用相同的方式删除，而只有一个左儿子的节点通过用其左子树上最大的节点替换，然后可将该节点删除。但是假如删除的节点不是红色的，那么就会破坏红黑树的平衡。解决的方法就是保证从上到下删除期间树叶是红色的。

在整个讨论中，令X为当前节点，T是它的兄弟，而P是它们的父亲。开始时我们把根涂成红色。当沿着树向下遍历时，我们设法保证X是红色的。当我们到达一个新的节点时，我们要确信P是红色的并且X和T是黑色的（因为不能有两个相连的红色节点）。存在两种主要情形。

情况一：X有两个黑色儿子。此时有三个子情况。

（1）T有两个黑儿子，那么我们可以翻转X、T、P的颜色来保持这种不变性。

（2）T的左儿子是红色的

（3）T的右儿子是红色的

情况二：X的儿子之一是红的。在这种情况下，我们落到下一层，得到新的X、T、P。如果幸运，X落在红儿子上。则我们继续前行。如果不是这样，那么我们知道T将是红的，而X和P将是黑的。我们可以旋转T和P，使得X的新父亲是红的；当然X和它的祖父是黑的。此时我们可以回到第一种主情况。

3.红黑树的实现

3.1 头文件

//
// RedBlackTree.h
// RedBlackTree3
//
// Created by Wuyixin on 2017/7/3.
// Copyright © 2017年 Coding365. All rights reserved.
// 

#ifndef RedBlackTree_h
#define RedBlackTree_h 

#include <stdio.h>
#include <stdlib.h>
#include <limits.h> 

typedef int ElementType; 

typedef enum {
 RED,
 BLACK
} COLOR; 

typedef struct RedBlackNode *RedBlackTree,*Position; 

struct RedBlackNode{
 ElementType Element;
 COLOR Color;
 RedBlackTree Left;
 RedBlackTree Right;
}; 

static Position NullNode = NULL;
static Position Header;
static Position X,P,GP,GGP;
/* 初始化 */
RedBlackTree Initialize();
/* 插入 */
RedBlackTree Insert(RedBlackTree T,ElementType Item);
/* 删除 */
RedBlackTree Remove(RedBlackTree T,ElementType Item);
/* 查找 */
Position Find(RedBlackTree T,ElementType Item);
/* 遍历 */
void Travel(RedBlackTree T); 

#endif /* RedBlackTree_h */ 

3.2 实现文件

//
// RedBlackTree.c
// RedBlackTree3
//
// Created by Wuyixin on 2017/7/3.
// Copyright © 2017年 Coding365. All rights reserved.
// 

#include "RedBlackTree.h" 

/* 左旋转 */
static Position SingleRotateLeft(Position X);
/* 右旋转 */
static Position SingleRotateRight(Position X);
/* 旋转 */
static Position Rotate(Position Parent,Position* Origin ,ElementType Item); 

/* 左旋转 */
static Position SingleRotateLeft(Position T){
 Position TL = T->Left;
 T->Left = TL->Right;
 TL->Right = T;
 return TL;
}
/* 右旋转 */
static Position SingleRotateRight(Position T){
 Position TR = T->Right;
 T->Right = TR->Left;
 TR->Left = T;
 return TR;
} 

/* 旋转 */
static Position Rotate(Position Parent,Position* Origin ,ElementType Item){
 if (Item < Parent->Element){
 if (Origin != NULL)
  *Origin = Parent->Left;
 return Parent->Left = Item < Parent->Left->Element ?
 SingleRotateLeft(Parent->Left) :
 SingleRotateRight(Parent->Left);
 }
 else{
 if (Origin != NULL)
  *Origin = Parent->Right;
 return Parent->Right = Item < Parent->Right->Element ?
 SingleRotateLeft(Parent->Right) :
 SingleRotateRight(Parent->Right);
 } 

} 

/* 初始化 */
RedBlackTree Initialize(){ 

 if (NullNode == NULL){
 NullNode = malloc(sizeof(struct RedBlackNode));
 if (NullNode == NULL)
  exit(EXIT_FAILURE);
 NullNode->Element = INT_MAX;
 NullNode->Color = BLACK;
 NullNode->Left = NullNode->Right = NullNode; 

 } 

 Header = malloc(sizeof(struct RedBlackNode));
 if (Header == NULL)
 exit(EXIT_FAILURE); 

 /* header的值为无穷小，所以根插入到右边*/
 Header->Element = INT_MIN;
 Header->Left = Header->Right = NullNode;
 Header->Color = BLACK; 

 return Header; 

} 

static Position GetSibling(Position Parent,Position X){
 if (Parent->Element == INT_MIN)
 return NULL;
 if (X == Parent->Left)
 return Parent->Right;
 else if (X == Parent->Right)
 return Parent->Left;
 else
 return NULL;
} 

void HandleReorientForInsert(ElementType Item){
 Position Sibling,Origin; 

 /* 当P与X同时为红节点才进行调整 */
 if (X == NullNode || !(P->Color == RED && X->Color == RED))
 return ; 

 Sibling = GetSibling(GP, P); 

 if (Sibling == NULL)
 return ; 

 /* GP,P,X是成字型，调整为一字型 */
 if ((GP->Element < Item) != (P->Element < Item)){
 P = Rotate(GP, &Origin,Item);
 X = Origin;
 } 

 GP = Rotate(GGP, &Origin,Item);
 P = Origin; 

 /* P的兄弟是黑色的 */
 if (Sibling->Color == BLACK){ 

 GP->Color = BLACK;
 GP->Left->Color = RED;
 GP->Right->Color = RED; 

 }
 /* P的兄弟是红的 */
 else{ 

 GP->Color = RED;
 GP->Left->Color = BLACK;
 GP->Right->Color = BLACK;
 }
} 

RedBlackTree _Insert(RedBlackTree T,ElementType Item){ 

 if (T == NullNode){
 T = malloc(sizeof(struct RedBlackNode));
 T->Element = Item;
 T->Left = T->Right = NullNode;
 T->Color = RED;
 }
 else if (Item < T->Element)
 T->Left = _Insert(T->Left, Item);
 else if (Item > T->Element)
 T->Right = _Insert(T->Right, Item);
 /* 重复值不插入 */ 

 X = P,P = GP,GP = GGP, GGP = T; 

 HandleReorientForInsert(Item); 

 return T;
} 

/* 插入 */
RedBlackTree Insert(RedBlackTree T,ElementType Item){
 GGP = GP = P = X = NullNode;
 T = _Insert(T, Item);
 T->Right->Color = BLACK;
 return T;
} 

static void _HandleReorientForRemove(ElementType Item){
 RedBlackTree Sibling,R;
 Sibling = GetSibling(P, X); 

 if (Sibling == NULL)
 return ; 

 if (Sibling->Left->Color == BLACK && Sibling->Right->Color == BLACK){
 P->Color = BLACK;
 X->Color = RED;
 Sibling->Color = RED;
 }else if(Sibling->Left->Color == RED){
 R = Sibling->Left; 

 P->Color = BLACK;
 X->Color = RED; 

 R = Rotate(P, NULL, R->Element);
 GP = Rotate(GP, NULL, R->Element); 

 }else if (Sibling->Right->Color == RED){
 X->Color = RED;
 P->Color = BLACK;
 Sibling->Color = RED;
 Sibling->Right->Color = BLACK; 

 GP = Rotate(GP, NULL, Sibling->Element); 

 }
} 

static void HandleReorientForRemove(RedBlackTree T, ElementType Item){
 RedBlackTree Sibling,Origin,OriginGP;
 if (X == NullNode)
 return ; 

 /* X有两个黑儿子 */
 if (X->Left->Color == BLACK && X->Right->Color == BLACK){
 _HandleReorientForRemove(Item);
 }else{ 

 OriginGP = GP;
 /* 落到下一层 */
 GP = P; P = X; 

 if (Item < X->Element)
  X = X->Left;
 else
  X = X->Right; 

 Sibling = GetSibling(P, X);
 /* 如果X是黑的，则Sibling是红的，旋转 */
 if (X->Color == BLACK){
  GP = Rotate(GP, &Origin, Sibling->Element);
  P = Origin;
  GP->Color = BLACK;
  P->Color = RED;
  _HandleReorientForRemove(Item); 

 } 

 /* 恢复X,PX,GP。由于X是当前节点 如果当前节点正是Item，不恢复会影响查找 */
 if (X->Element == Item){
  X = P ; P = GP ;GP = OriginGP;
 } 

 }
} 

/* 删除 */
RedBlackTree Remove(RedBlackTree T,ElementType Item){ 

 ElementType Origin;
 Position DeletePtr;
 Origin = NullNode->Element; 

 NullNode->Element = Item; 

 GP = P = X = T; 

 /* 根染红 */
 T->Right->Color = RED; 

 while (X->Element != Item) {
 GP = P ; P = X;
 if (Item < X->Element)
  X = X->Left;
 else
  X = X->Right; 

 HandleReorientForRemove(T, Item);
 } 

 NullNode->Element = Origin; 

 /* 找到 */
 if (X != NullNode){
 DeletePtr = X;
 if (X->Left != NullNode){
  GP = P ; P = X; X = X->Left;
  HandleReorientForRemove(T, Item);
  /* 寻找左子树最大值替换 */
  while (X->Right != NullNode) {
  GP = P ; P = X;
  X = X->Right;
  HandleReorientForRemove(T, Item);
  }
  if (X == P->Left)
  P->Left = X->Left;
  else
  P->Right = X->Left; 

 }else if (X->Right != NullNode){
  GP = P ; P = X; X = X->Right;
  HandleReorientForRemove(T, Item);
  /* 寻找右子树最大值替换 */
  while (X->Left != NullNode) {
  GP = P ; P = X;
  X = X->Left;
  HandleReorientForRemove(T, Item);
  }
  if (X == P->Left)
  P->Left = X->Right;
  else
  P->Right = X->Right;
 }else{
  /* X是树叶 */
  if (X == P->Left)
  P->Left = NullNode;
  else
  P->Right = NullNode;
 } 

 DeletePtr->Element = X->Element;
 free(X); 

 } 

 /* 根染黑 */
 T->Right->Color = BLACK; 

 return T;
} 

typedef enum {
 ROOT,
 LEFT,
 RIGHT
} NodeType; 

static char *TypeC;
static char *ColorC; 

void _Travel(RedBlackTree T , NodeType Type){ 

 if (T != NullNode){ 

 if (Type == ROOT)
  TypeC = "root";
 else if (Type == LEFT)
  TypeC = "left";
 else if (Type == RIGHT)
  TypeC = "right"; 

 if (T->Color == BLACK)
  ColorC = "black";
 else
  ColorC = "red"; 

 printf("(%d,%s,%s) ",T->Element,ColorC,TypeC); 

 _Travel(T->Left, LEFT);
 _Travel(T->Right, RIGHT); 

 } 

} 

/* 遍历 */
void Travel(RedBlackTree T){
 _Travel(T->Right,ROOT);
} 

3.3 调用

//
// main.c
// RedBlackTree3
//
// Created by Wuyixin on 2017/7/3.
// Copyright © 2017年 Coding365. All rights reserved.
// 

#include "RedBlackTree.h"
int main(int argc, const char * argv[]) { 

  RedBlackTree T = Initialize(); 

  T = Insert(T, 10);
  T = Insert(T, 85);
  T = Insert(T, 15);
  T = Insert(T, 70);
  T = Insert(T, 20);
  T = Insert(T, 60);
  T = Insert(T, 30);
  T = Insert(T, 50);
  T = Insert(T, 65);
  T = Insert(T, 80);
  T = Insert(T, 90);
  T = Insert(T, 40);
  T = Insert(T, 5);
  T = Insert(T, 55);
  T = Insert(T, 100); 

  T = Remove(T, 100); 

  Travel(T); 

  return 0;
} 

以上就是关于数据结构与算法中红黑二叉树的详解，如有疑问请留言或者到本站的社区讨论，感谢阅读，希望能帮助到大家，谢谢大家对本站的支持！