C语言超详细讲解排序算法下篇
上期学习完了前四个排序，这期我们来学习剩下的三个排序：
🍔 1、冒泡排序
🍟 2、快速排序 ( 三种方法 )
🍞 3、归并排序
🧀 4、排序算法复杂度及稳定性分析
今天我们主要难点有快速排序和归并排序，会简单涉及到二叉树相关知识，相对来说比较抽象！所以如果有看不懂或者不明白的地方可以看看我之前的详解二叉树，也可以直接问我！教你打篮球的程序猿随时在线。👴
🍔 1、冒泡排序
冒泡排序是我们相对最好理解的个排序，但是有些小优化的地方我会指出来，我们先看图解：
void BubbleSort(int* a, int n)//升序{//时间复杂度O(N^2)while (n > 0){int exchange = 0;for (int i = 1; i < n; ++i)//防止越界访问{if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);//交换exchange = 1;}}if (exchange == 0){break;}--n;}}代码分析：我们每排完一趟，就可以确定最后一个位置的数，再者我们定义了一个exchange来判断在排序过程中是否发生了交换，如果没有发生交换，证明此数组已经有序，我们可以直接跳出循环，避免不必要的循环！
冒泡排序的特性总结：
1. 冒泡排序是一种非常容易理解的排序
2. 时间复杂度：O(N^2) 、空间复杂度：O(1)
3. 稳定性：稳定
🍟 2、快速排序 ( 三种方法 )
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法。
基本思想为：任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。
第一种方法是我们最常见的挖坑法：
代码实现如下：
void QuickSort(int* a, int left, int right)//升序{if (left >= right){return;}int begin = left;int end = right;int pivot = begin;int key = a[begin];while (begin < end){//右边找小while (begin < end && a[end] >= key) //这里如果不写begin<end的话可能会出现越界访问{--end;}//小的放到左边的坑里，自己形成了新的坑位a[pivot] = a[end];pivot = end; //左边找大while (begin < end && a[begin] <= key){++begin;}//大的放到左边的坑里，自己形成了新的坑位a[pivot] = a[begin];pivot = begin;}//当begin和end相遇，证明他们两都到了坑的位置pivot = begin;//随便给一个a[pivot] = key;//[left, pivot - 1] pivot [pivot+ 1, right]//左子区间和右子区间有序，我们就有序了，如何让他们有序呢？分治递归QuickSort(a, left, key - 1);QuickSort(a, key + 1, right);}//函数传参：QuickSort(arr, 0, sizeof(arr) / sizeof(int) - 1);第二种方法左右指针法：
代码实现如下：
void QuickSort(int* a, int left, int right)//升序{if (left >= right){return;}int begin = left;int end = right;int keyi = begin;while (begin < end){//找小while (begin < end && a[end] >= a[keyi]){--end;}//找大while (begin < end && a[begin] <= a[keyi]){++begin;}Swap(&a[begin], &a[end]);}Swap(&a[begin], &a[keyi]);keyi = begin;//[left, keyi - 1] keyIndex [keyi + 1, right]//左子区间和右子区间有序，我们就有序了，如何让他们有序呢？分治递归QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);}第三种方法前后指针法：
代码实现如下：
void QuickSort(int* a, int left, int right)//升序{if (left >= right){return;}int keyi = left;int prev = left;int cur = left + 1;while (cur <= right){ //++prev != cur为了防止自己跟自己交换造成不必要的消耗if (a[cur] < a[keyi] && ++prev != cur){Swap(&a[prev], &a[cur]);}++cur;}Swap(&a[keyi], &a[prev]);keyi = prev;//[left, keyi - 1] keyi [keyi + 1, right]//左子区间和右子区间有序，我们就有序了，如何让他们有序呢？分治递归QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);}🍞 3、归并排序
基本思想： 归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法,该算法是采用分治法 （Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。
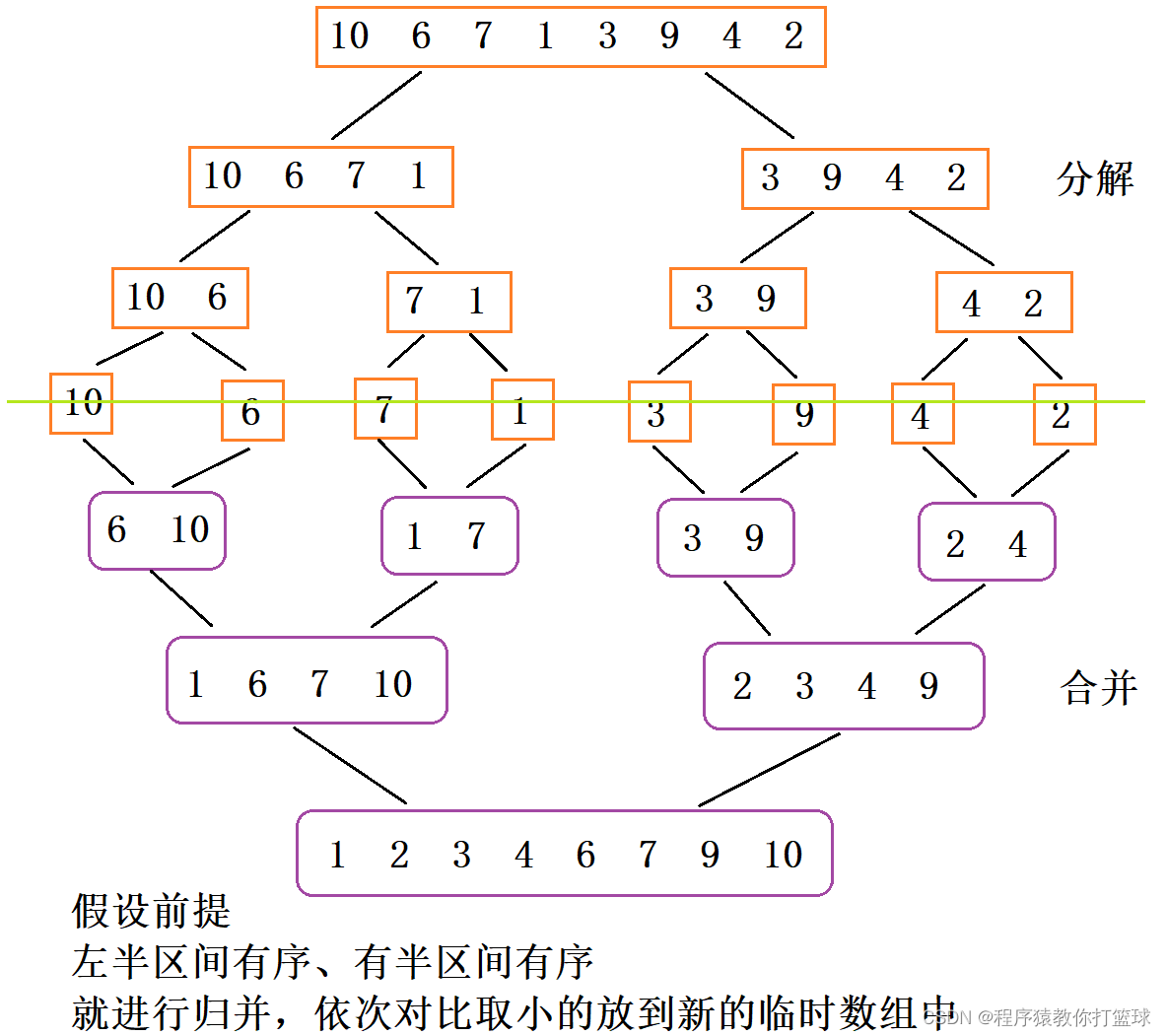
归并排序我们思想还是和快排思想差不多采用分治算法，当数组被分为单独一个元素就是有序的了(见上图)，在接着归并到一个数组中，即可实现排序！
代码实现如下：
void _MergeSort(int* a, int left, int right, int* tmp){if (left >= right)return;int mid = (left + right) >> 1;// 假设[left, mid] [mid + 1, right] 有序，那么我们就可以归并了_MergeSort(a, left, mid, tmp);_MergeSort(a, mid + 1, right, tmp);//归并int begin1 = left, end1 = mid;int begin2 = mid + 1, end2 = right;int index = left;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[index++] = a[begin1++];}else{tmp[index++] = a[begin2++];}}while (begin1 <= end1){tmp[index++] = a[begin1++];}while (begin2 <= end2){tmp[index++] = a[begin2++];}//拷贝回去for (int i = left; i <= right; ++i){a[i] = tmp[i];}}void MergeSort(int* a, int n){int* tmp = (int*)malloc(sizeof(int) * n);_MergeSort(a, 0, n - 1, tmp);free(tmp);}🧀 4、排序算法复杂度及稳定性分析
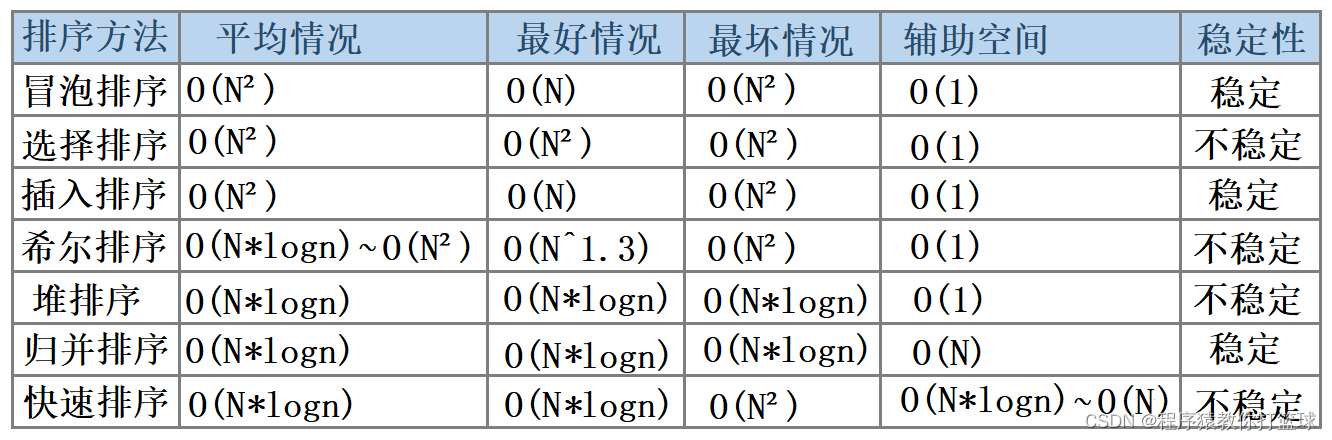
稳定性：假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍 在r[j]之前，则称这种排序算法是稳定的；否则称为不稳定的。
I can do all things（我能做成任何事！）相信自己，加油！
联系方式(qq)：623847465 gitee(码云)：Mercury. (zzwlwp) - Gitee.com
相关推荐
-
C语言数据结构经典10大排序算法刨析
1.冒泡排序 // 冒泡排序 #include <stdlib.h> #include <stdio.h> // 采用两层循环实现的方法. // 参数arr是待排序数组的首地址,len是数组元素的个数. void bubblesort1(int *arr,unsigned int len) { if (len<2) return; // 数组小于2个元素不需要排序. int ii; // 排序的趟数的计数器. int jj; // 每趟排序的元素位置计数器. int itmp
-
C语言直接插入排序算法
目录 1.算法模板 2.算法介绍 3.实例 总结 1.算法模板 void InsertSort(SqList *L) { int j; for (int i = 2; i <= L->length; i ++ ) { if (L->arr[i] < L->arr[i-1]) { L->arr[0] = L->arr[i]; // 设置哨兵 for (j = i - 1; L->arr[j] > L->arr[0]; j -- ) L->ar
-
C语言直接插入排序算法介绍
目录 前言 一.什么是直接插入排序 二.代码讲解 总结 前言 直接 插入排序 (Straight Insertion Sort)是一种最简单的排序方法,其基本操作是将一条记录插入到已排好的有序表中,从而得到一个新的.记录数量增1的有序表.. 废话不多说先看看代码 #define _CRT_SECURE_NO_WARNINGS 1 //直接插入排序法 #include <stdio.h> void Compare(int arr[], int len) { int i = 0; for (i =
-
C语言中冒泡排序算法详解
目录 一.算法描述 二.算法分析 三.完整代码 总结 一.算法描述 比较相邻两个元素,如果第一个比第二个大则交换两个值.遍历所有的元素,每一次都会将未排序序列中最大的元素放在后面.假设数组有 n 个元素,那么需要遍历 n - 1 次,因为剩下的一个元素一定是最小的,无需再遍历一次.因此需要两层循环,第一层是遍历次数,第二层是遍历未排序数组. 动图如下: 黄色部分表示已排好序的数组,蓝色部分表示未排序数组 核心代码如下: /** * @brief 冒泡排序 * * @param arr 待排序的数
-
C语言实现单链表的快速排序算法
目录 背景 设计思路 算法主要步骤 快速排序算法实现 整个程序源代码 测试案例 总结 背景 传统QuickSort算法最大不足之处在于,由于其基于可索引存储结构设计(一般为数组或索引表),因而无法用于链式存储结构,而链式存储结构的实际应用非常广泛,例如动态存储管理.动态优先级调度等等,故本文针对于单向链表,以QuickSort的分治策略为基础,提出一种可用于单向链表的快速排序算法. 设计思路 将单向链表的首节点作为枢轴节点,然后从单向链表首部的第二个节点开始,逐一遍历所有后续节点,并将这些已遍历
-
C语言之直接插入排序算法的方法
目录 一.什么是直接插入排序 二.代码讲解 总结 直接 插入排序 (Straight Insertion Sort)是一种最简单的排序方法,其基本操作是将一条记录插入到已排好的有序表中,从而得到一个新的.记录数量增1的有序表.. 废话不多说先看看代码 #define _CRT_SECURE_NO_WARNINGS 1 //直接插入排序法 #include <stdio.h> void Compare(int arr[], int len) { int i = 0; for (i = 0; i
-
C语言冒泡排序算法代码详解
今天我们来用C语言实现一下冒泡排序 首先我们来了解一下什么叫做冒泡排序,冒泡顾名思义把质量轻的气体(如二氧化碳一样)浮到水面上(如可乐中的二氧化碳),因此冒泡排序的原理就是N个元素在一个周期中,微观上依次进行两两元素的比较,小的元素就被放在前面,大的元素放在后面,以此来进行N-1个周期,来完成冒泡排序. 上文中的一个周期,即外循环,依次进行比较,即内循环. 文字看着很迷糊?没事儿,上图 如图所示,两两元素依次进行比较,小的元素往前移动,大的元素往后移动,直至元素顺序是升序的形式,即移动了 元素-
-
C语言库函数qsort及bsearch快速排序算法使用解析
目录 qsort 含义 实现 格局打开 bsearch qsort qsrot 就是C语言库函数中的快速排序函数,对数组,结构体都可以实现快速排序, 他在头文件<stdlib.h>中使用,声明格式为: void qsort(void* base, size_t nums, size_t size, int (*compare)(const void *, const void*)) 这么烦人一长串的参数各是什么意思呢,base 是指向要排序的数组的第一个元素的指针.nums是由 base 指向
-
C语言超详细梳理排序算法的使用
目录 排序的概念及其运用 排序的概念 排序运用 插入排序 直接插入排序 希尔排序 选择排序 直接选择排序 堆排序 交换排序之冒泡排序 总结 排序的概念及其运用 排序的概念 排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作. 稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次 序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排 序算法
-
C语言超详细讲解排序算法下篇
上期学习完了前四个排序，这期我们来学习剩下的三个排序：
-
C语言超详细讲解排序算法上篇
目录 1.直接插入排序 2.希尔排序(缩小增量排序) 3.直接选择排序 4.堆排序 进入正式内容之前,我们先了解下初阶常见的排序分类 :我们今天讲前四个! 1.直接插入排序 基本思想:当插入第i(i>=1)个元素时,前面的array[0],array[1],…,array[i-1]已经排好序,此时用array[i]的排 序码与array[i-1],array[i-2],…的排序码顺序进行比较,找到插入位置即将array[i]插入,原来位置上的元素顺序后移! 直接插入排序的特性总结: 1. 元素集
-
C语言 超详细讲解算法的时间复杂度和空间复杂度
目录 1.前言 1.1 什么是数据结构? 1.2 什么是算法? 2.算法效率 2.1 如何衡量一个算法的好坏 2.2 算法的复杂度 2.3 复杂度在校招中的考察 3.时间复杂度 3.1 时间复杂度的概念 3.2 大O的渐进表示法 3.3 常见时间复杂度计算举例 4.空间复杂度 5. 常见复杂度对比 1.前言 1.1 什么是数据结构? 数据结构(Data Structure)是计算机存储.组织数据的方式,指相互之间存在一种或多种特定关系的数据元素的集合. 1.2 什么是算法? 算法(Algorit
-
C语言超详细讲解数据结构中双向带头循环链表
目录 一.概念 二.必备工作 2.1.创建双向链表结构 2.2.初始化链表 2.3.动态申请节点 2.4.打印链表 2.5.销毁链表 三.主要功能 3.1.在pos节点前插入数据 尾插 头插 3.2.删除pos处节点数据 尾删 头删 3.3.查找数据 四.总代码 List.h 文件 List.c 文件 Test.c 文件 五.拓展 一.概念 前文我们已经学习了单向链表,并通过oj题目深入了解了带头节点的链表以及带环链表,来画张图总体回顾下: 在我们学习的链表中,其实总共有8种,都是单双向和带不带
-
C语言超详细讲解字符串相乘
目录 前言 一. 分析思路 二.使用步骤 1.代码如下 2.memset函数 三.总结 前言 我们已经知道,正常的两位整形数据通过*相乘,C语言中int为4字节,32bit(字节),其机器码第一位为符号位,余下31位表示数字,表示范围:-2^31(-2147483648)~2^31-1(2147483647),但超过了这个范围我们该如何做呢? 提示:将数字以字符串的形式进行操作 一. 分析思路 示例: 我们把每一个数都看成是一个字符串,每一个元素为十进制数字所对应的字 符,由于是后面的元素先进行
-
C语言超详细讲解轮转数组
目录 题目描述 实例 解题思路 1. 先整体逆转 2.逆转子数组[0, k - 1] 3.逆转子数组[k, numsSize - 1] 易错点 代码 题目描述 给你一个数组,将数组中的元素向右轮转 k 个位置,其中 k 是非负数.OJ链接 实例 1.实例1 输入: nums = [1,2,3,4,5,6,7], k = 3输出: [5,6,7,1,2,3,4]解释:向右轮转 1 步: [7,1,2,3,4,5,6]向右轮转 2 步: [6,7,1,2,3,4,5]向右轮转 3 步: [5,6,7
-
C语言超详细文件操作基础下篇
目录 一.文件的顺序读写 1.格式化的输出函数(fprintf) 2.格式化的输入函数(fscanf) 3.二进制读写 1.二进制输出函数(fwrite) 2.二进制输入函数 3.scanf,fscanf,sscanf.printf,fprintf,sprintf的区别 二.文件的随机读写 1.fseek函数 2.ftell函数 3.rewind函数 三.被错误使用的feof 总结 一.文件的顺序读写 兄弟们,上一章只介绍到了如何把单个的字符或者字符串如何写到文件里或者从文件中读取,文件的顺序读
-
C语言 超详细讲解链接器
目录 1 什么是链接器 2 声明与定义 3 命名冲突 3.1 命名冲突 3.2 static修饰符 4 形参.实参.返回值 5 检查外部类型 6 头文件 1 什么是链接器 典型的链接器把由编译器或汇编器生成的若干个目标模块,整合成一个被称为载入模块或可执行文件的实体–该实体能够被操作系统直接执行. 链接器通常把目标模块看成是由一组外部对象组成的.每个外部对象代表着机器内存中的某个部分,并通过一个外部名称来识别.因此,==程序中的每个函数和每个外部变量,如果没有被声明为static,就都是一个外部
-
C语言 超详细讲解库函数
目录 1 返回整数的getchar函数 2 更新顺序文件 3 缓冲输出与内存分配 4 库函数 练习 1 返回整数的getchar函数 代码: #include<stdio.h> int main() { char c; while((c = getchar())!=EOF)//getchar函数的返回值为整型 putchar(c); return 0; } 上述代码有三种可能: 某些合法的输入字符在被"截断"后使得c的取值与EOF相同,程序将在复制的中途停止. c根本不可能