C语言动态规划多种背包问题分析讲解

目录

• 写在前面
• 01背包问题
• 完全背包问题
• 多重背包问题 I
• 多重背包问题 II
• 为什么可以这样优化呢
• 一 、二进制与十进制
• 二 、动态规划的时间复杂度估算
• 三 、多重背包
• 分组背包问题

写在前面

之前讲过简单DP，经典01背包问题，在这我将会把背包问题更深入的讲解，希望能帮助大家更好的理解。

01背包问题

C语言数学问题与简单DP01背包问题详解

先回忆一下这个图

在这我再将01背包问题代码发一遍，可以用来做对比。

二维：

#include<bits/stdc++.h>

using namespace std;

const int MAXN = 1005;
int v[MAXN];    // 体积
int w[MAXN];    // 价值
int f[MAXN][MAXN];  // f[i][j], j体积下前i个物品的最大价值 

int main()
{
    int n, m;
    cin >> n >> m;
    for(int i = 1; i <= n; i++)
        cin >> v[i] >> w[i];

    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++)
        {
            //  当前背包容量装不进第i个物品，则价值等于前i-1个物品
            if(j < v[i])
                f[i][j] = f[i - 1][j];
            // 能装，需进行决策是否选择第i个物品
            else
                f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
        }           

    cout << f[n][m] << endl;

    return 0;
}

一维：

#include<bits/stdc++.h>

using namespace std;

const int MAXN = 1005;
int f[MAXN];  // 

int main()
{
    int n, m;
    cin >> n >> m;

    for(int i = 1; i <= n; i++) {
        int v, w;
        cin >> v >> w;      // 边输入边处理
        for(int j = m; j >= v; j--)
            f[j] = max(f[j], f[j - v] + w);
    }

    cout << f[m] << endl;

    return 0;
}

完全背包问题

完全背包问题和01背包问题的区别就在于完全背包问题中每件物品都有无限件可用。我们也可以先来试一下暴力写法。

#include<iostream>
using namespace std;

const int N = 1010;

int n, m;
int dp[N][N], v[N], w[N];

int main(){
    cin >> n >> m;
    for(int i = 1; i <= n; i ++ )
        cin >> v[i] >> w[i];

    for(int i = 1; i <= n; i ++ )
        for(int j = 0; j <= m; j ++ )
            for(int k = 0; k * v[i] <= j; k ++ )//因为每一件物品都有无限件可用，我们只需要找出单件价值最高的商品就可以了
                dp[i][j] = max(dp[i][j], dp[i - 1][j - k * v[i]] + k * w[i]);
    cout << dp[n][m] << endl;
}

优化思路：

我们列举一下更新次序的内部关系：

f[i , j ] = max( f[i-1,j] , f[i-1,j-v]+w , f[i-1,j-2v]+2w , f[i-1,j-3v]+3w , …)

f[i , j-v]= max( f[i-1,j-v] , f[i-1,j-2v] + w , f[i-1,j-3v]+2*w , …)

由上两式，可得出如下递推关系：

f[i][j]=max(f[i,j-v]+w , f[i-1][j])

有了上面的关系，那么其实k循环可以不要了，核心代码优化成这样：

for(int i = 1 ; i <=n ;i++)
for(int j = 0 ; j <=m ;j++)
{
    f[i][j] = f[i-1][j];
    if(j-v[i]>=0)
        f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);
}

这个代码和01背包的非优化写法很像啊!!!我们对比一下，下面是01背包的核心代码

for(int i = 1 ; i <= n ; i++)
for(int j = 0 ; j <= m ; j ++)
{
    f[i][j] = f[i-1][j];
    if(j-v[i]>=0)
        f[i][j] = max(f[i][j],f[i-1][j-v[i]]+w[i]);
}

两个代码其实只有一句不同（注意下标）

f[i][j] = max(f[i][j],f[i-1][j-v[i]]+w[i]);//01背包

f[i][j] = max(f[i][j],f[i][j-v[i]]+w[i]);//完全背包问题

因为和01背包代码很相像，我们很容易想到进一步优化。核心代码可以改成下面这样

for(int i = 1 ; i<=n ;i++)
    for(int j = v[i] ; j<=m ;j++)//注意了，这里的j是从小到大枚举，和01背包不一样
    {
            f[j] = max(f[j],f[j-v[i]]+w[i]);
    }

综上所述，完全背包的最终写法如下：

#include<iostream>
using namespace std;
const int N = 1010;
int f[N];
int v[N],w[N];
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i = 1 ; i <= n ;i ++)
    {
        cin>>v[i]>>w[i];
    }

    for(int i = 1 ; i<=n ;i++)
    for(int j = v[i] ; j<=m ;j++)
    {
            f[j] = max(f[j],f[j-v[i]]+w[i]);
    }
    cout<<f[m]<<endl;
}

多重背包问题 I

我们先来看这多重背包问题和01背包问题是不是很像，将s×v，s×w是不是就可以看成01背包问题了？

for(ll i=1;i<=n;i++)
    {
        cin>>a>>b>>c;
        for(ll j=1;j<=c;j++)
        {
            v[cnt]=a;
            w[cnt]=b;
            cnt++;
        }//将多重背包一个一个拆出来
    }

然后转换成01背包问题解决。

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;

const ll N=1e5+100;

ll v[N],w[N];
ll f[N];
int main()
{
    ll n,m;
    ll cnt=1;
    cin>>n>>m;
    ll a,b,c;
    for(ll i=1;i<=n;i++)
    {
        cin>>a>>b>>c;
        for(ll j=1;j<=c;j++)
        {
            v[cnt]=a;
            w[cnt]=b;
            cnt++;
        }//将多重背包一个一个拆出来
    }
    for(ll i=1;i<=cnt;i++)
    {
        for(ll j=m;j>=v[i];j--)
        {
            f[j]=max(f[j],f[j-v[i]]+w[i]);
        }
    }//01背包
    cout<<f[m];
    return 0;
}

多重背包问题 II

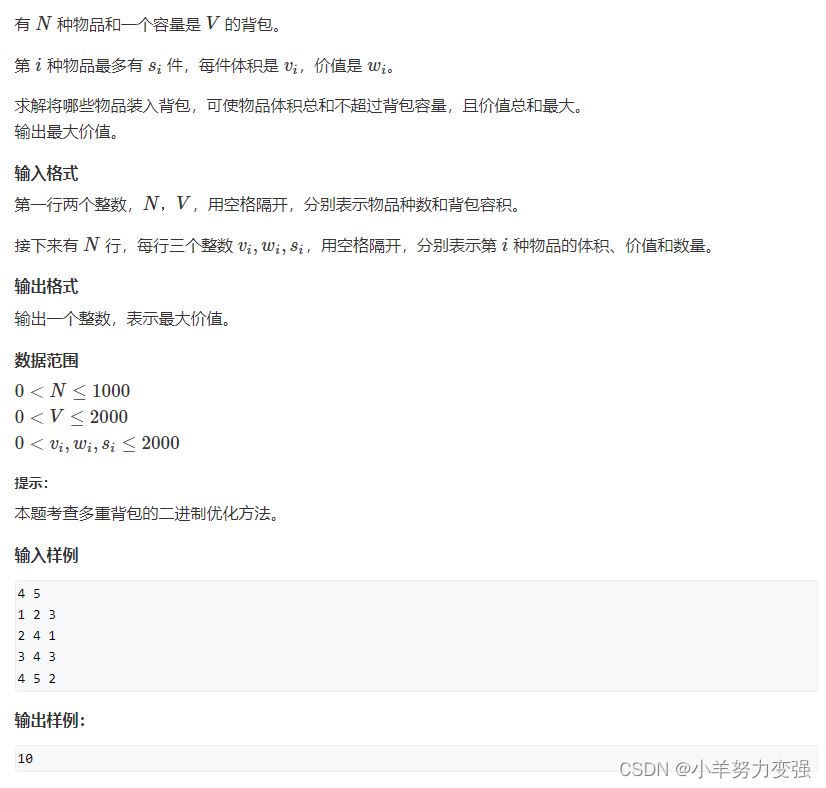
这道题和1看起来没什么区别，但是数据范围变了，数据范围变了如果不优化就话超时，那怎么优化呢？

我们只需要将转换成01背包问题那一部分优化了就可以了。

int cnt = 0;     // 将物品重新分组后的顺序
    for (int i = 1; i <= n; i ++)
    {
        int a, b, s;    // a 体积, b 价值, s 每种物品的个数
        scanf("%d %d %d", &a, &b, &s);

        int k = 1;   // 二进制拆分 打包时每组中有 k 个同种物品
        while (k <= s)  // 即y总说的: 最后一组的物品个数 < 2^(n+1)   1 2 4 8 16 ... 2^n 2^(n+1)
        {
            cnt ++;
            v[cnt] = a * k;  // 每组的体积
            w[cnt] = b * k;  // 每组的价值
            s -= k;
            k *= 2;  // 注意是 k * 2，每次增长一倍，不是k * k
        }

        if (s > 0)   // 二进制拆分完之后 剩下的物品个数分为新的一组
        {
            cnt ++;
            v[cnt] = a * s;
            w[cnt] = b * s;
        }
    }

为什么可以这样优化呢

我们知道任何一个数都可以转化成二进制的数，那二进制和十进制的区别在哪呢?

一 、二进制与十进制

• 普通遍历问题

遍历 n 个物品, 采用二进制计数方法遍历与采用十进制技术方法遍历的时间复杂度是一样的

举例来说, 对于十进制数 8

十进制遍历: 0,1,2,3,4,5,6,7 共 8 次遍历

二进制遍历: 000, 001, 010, 011, 100, 101, 110, 111 共 8 次遍历

• 多重背包问题

同样的道理, 对于多重背包问题, 采用二进制的遍历方法不能优化时间复杂度

优化的原因在于引入了动态规划

二 、动态规划的时间复杂度估算

动态规划的时间复杂度 ≈≈ 问题的总个数 × 问题要做出的选择数

如, 对于 01 背包问题, 问题的总个数为N⋅V (N 为物品个数, V 为背包容量), 问题要做出的选择数为 2(选或不选)

则 01 背包问题的时间复杂度约为 2N⋅V

三 、多重背包

如果不采用动态规划的做法, 就像普通的遍历问题那样, 是否采用二进制的计数方法对时间复杂度的优化没有任何关系

但采用二进制的计数方法会影响问题的总个数与问题的选择数的乘积, 即动态规划做法下多重背包的时间复杂度

多重背包的动态规划时间复杂度

十进制遍历方法

问题的总个数为 N⋅V, N 为物品的种类数, V 为背包容量

问题的选择数约为 Smax,Smax 为每种物品数量的最大值

十进制下多重背包问题的 DP 时间复杂度为: N⋅V⋅Smax

二进制遍历方法

十进制下, 一种物品有 si个, 二进制下, 变为 1, 2, … , lgsi 个物品, 则共有 lgs1+lgs2+…+lg⁡sn 个物品, 约为 Nlgsmax 个物品

问题的总个数为 N⋅V⋅lgsmax

问题的选择数为 2

十进制下多重背包问题的 DP 时间复杂度为: 2N⋅V⋅lgsmax

最后请看代码

#include <bits/stdc++.h>

using namespace std;

const int N = 11 * 1000 + 10, M = 2010;

int v[N], w[N];
int f[M];

int main()
{
    int  n, m;
    scanf("%d %d", &n, &m);

    int cnt = 0;     // 将物品重新分组后的顺序
    for (int i = 1; i <= n; i ++)
    {
        int a, b, s;    // a 体积, b 价值, s 每种物品的个数
        scanf("%d %d %d", &a, &b, &s);

        int k = 1;   // 二进制拆分 打包时每组中有 k 个同种物品
        while (k <= s)  // 即y总说的: 最后一组的物品个数 < 2^(n+1)   1 2 4 8 16 ... 2^n 2^(n+1)
        {
            cnt ++;
            v[cnt] = a * k;  // 每组的体积
            w[cnt] = b * k;  // 每组的价值
            s -= k;
            k *= 2;  // 注意是 k * 2，每次增长一倍，不是k * k
        }

        if (s > 0)   // 二进制拆分完之后 剩下的物品个数分为新的一组
        {
            cnt ++;
            v[cnt] = a * s;
            w[cnt] = b * s;
        }
    }

    n = cnt;  // 所有的组数即为 01背包中的物品个数

    // 写01背包模板
    for (int i = 1; i <= n; i ++)
        for (int j = m; j >= v[i]; j --)
            f[j] = max(f[j], f[j - v[i]] + w[i]);

    printf("%d", f[m]);

    return 0;
}

分组背包问题

• 状态表示：f[i][j]

集合：从前i组物品中选,且总体积不超过j的所有方案的集合.

属性：最大值

• 状态计算：

思想-----集合的划分

集合划分依据：根据从第i组物品中选哪个物品进行划分.

f[i][j] = max(f[i][j], f[i - 1][j - v[i][k]] + w[i][k]);

请看代码

#include<bits/stdc++.h>
using namespace std;

const int N=110;
int f[N][N];  //只从前i组物品中选，当前体积小于等于j的最大值
int v[N][N],w[N][N],s[N];   //v为体积，w为价值，s代表第i组物品的个数
int n,m,k;

int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        cin>>s[i];
        for(int j=0;j<s[i];j++){
            cin>>v[i][j]>>w[i][j];  //读入
        }
    }

    for(int i=1;i<=n;i++){
        for(int j=0;j<=m;j++){
            f[i][j]=f[i-1][j];  //不选 不选表示不选第 i 组物品的所有物品，只从前 i−1 组物品里面选
            for(int k=0;k<s[i];k++){
                if(j>=v[i][k])     f[i][j]=max(f[i][j],f[i-1][j-v[i][k]]+w[i][k]);
            }
        }
    }
    cout<<f[n][m]<<endl;
}

因为只用到了第i-1列，所以可以仿照01背包的套路逆向枚举体积

#include<bits/stdc++.h>
using namespace std;

const int N=110;
int f[N];
int v[N][N],w[N][N],s[N];
int n,m,k;

int main(){
    cin>>n>>m;
    for(int i=0;i<n;i++){
        cin>>s[i];
        for(int j=0;j<s[i];j++){
            cin>>v[i][j]>>w[i][j];
        }
    }

    for(int i=0;i<n;i++){
        for(int j=m;j>=0;j--){
            for(int k=0;k<s[i];k++){    //for(int k=s[i];k>=1;k--)也可以
                if(j>=v[i][k])     f[j]=max(f[j],f[j-v[i][k]]+w[i][k]);
            }
        }
    }
    cout<<f[m]<<endl;
}

到此这篇关于C语言动态规划多种背包问题分析讲解的文章就介绍到这了,更多相关C语言 背包问题内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！