利用python做数据拟合详情

目录

• 1、例子：拟合一种函数Func，此处为一个指数函数。
• 2. 例子：拟合一个Gaussian函数
• 3. 用一个lmfit的包来实现2中的Gaussian函数拟合

1、例子：拟合一种函数Func，此处为一个指数函数。

出处：

SciPy v1.1.0 Reference Guide

#Header
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit

#Define a function(here a exponential function is used)
def func(x, a, b, c):
 return a * np.exp(-b * x) + c

#Create the data to be fit with some noise
xdata = np.linspace(0, 4, 50)
y = func(xdata, 2.5, 1.3, 0.5)
np.random.seed(1729)
y_noise = 0.2 * np.random.normal(size=xdata.size)
ydata = y + y_noise
plt.plot(xdata, ydata, 'bo', label='data')

#Fit for the parameters a, b, c of the function func:
popt, pcov = curve_fit(func, xdata, ydata)
popt #output: array([ 2.55423706, 1.35190947, 0.47450618])
plt.plot(xdata, func(xdata, *popt), 'r-',
 label='fit: a=%5.3f, b=%5.3f, c=%5.3f' % tuple(popt))

#In the case of parameters a,b,c need be constrainted
#Constrain the optimization to the region of
#0 <= a <= 3, 0 <= b <= 1 and 0 <= c <= 0.5
popt, pcov = curve_fit(func, xdata, ydata, bounds=(0, [3., 1., 0.5]))
popt #output: array([ 2.43708906, 1. , 0.35015434])
plt.plot(xdata, func(xdata, *popt), 'g--',
 label='fit: a=%5.3f, b=%5.3f, c=%5.3f' % tuple(popt))

#Labels
plt.title("Exponential Function Fitting")
plt.xlabel('x coordinate')
plt.ylabel('y coordinate')
plt.legend()
leg = plt.legend()  # remove the frame of Legend, personal choice
leg.get_frame().set_linewidth(0.0) # remove the frame of Legend, personal choice
#leg.get_frame().set_edgecolor('b') # change the color of Legend frame
#plt.show()

#Export figure
#plt.savefig('fit1.eps', format='eps', dpi=1000)
plt.savefig('fit1.pdf', format='pdf', dpi=1000, figsize=(8, 6), facecolor='w', edgecolor='k')
plt.savefig('fit1.jpg', format='jpg', dpi=1000, figsize=(8, 6), facecolor='w', edgecolor='k')

上面一段代码可以直接在spyder中运行。得到的JPG导出图如下：

2. 例子：拟合一个Gaussian函数

出处：LMFIT: Non-Linear Least-Squares Minimization and Curve-Fitting for Python

#Header
import numpy as np
import matplotlib.pyplot as plt
from numpy import exp, linspace, random
from scipy.optimize import curve_fit

#Define the Gaussian function
def gaussian(x, amp, cen, wid):
 return amp * exp(-(x-cen)**2 / wid)

#Create the data to be fitted
x = linspace(-10, 10, 101)
y = gaussian(x, 2.33, 0.21, 1.51) + random.normal(0, 0.2, len(x))
np.savetxt ('data.dat',[x,y])  #[x,y] is is saved as a matrix of 2 lines

#Set the initial(init) values of parameters need to optimize(best)
init_vals = [1, 0, 1] # for [amp, cen, wid]

#Define the optimized values of parameters
best_vals, covar = curve_fit(gaussian, x, y, p0=init_vals)
print(best_vals) # output: array [2.27317256  0.20682276  1.64512305]

#Plot the curve with initial parameters and optimized parameters
y1 = gaussian(x, *best_vals) #best_vals, '*'is used to read-out the values in the array
y2 = gaussian(x, *init_vals) #init_vals
plt.plot(x, y, 'bo',label='raw data')
plt.plot(x, y1, 'r-',label='best_vals')
plt.plot(x, y2, 'k--',label='init_vals')
#plt.show()

#Labels
plt.title("Gaussian Function Fitting")
plt.xlabel('x coordinate')
plt.ylabel('y coordinate')
plt.legend()
leg = plt.legend()  # remove the frame of Legend, personal choice
leg.get_frame().set_linewidth(0.0) # remove the frame of Legend, personal choice
#leg.get_frame().set_edgecolor('b') # change the color of Legend frame
#plt.show()

#Export figure
#plt.savefig('fit2.eps', format='eps', dpi=1000)
plt.savefig('fit2.pdf', format='pdf', dpi=1000, figsize=(8, 6), facecolor='w', edgecolor='k')
plt.savefig('fit2.jpg', format='jpg', dpi=1000, figsize=(8, 6), facecolor='w', edgecolor='k')

上面一段代码可以直接在spyder中运行。得到的JPG导出图如下：

3. 用一个lmfit的包来实现2中的Gaussian函数拟合

需要下载lmfit这个包，下载地址：

https://pypi.org/project/lmfit/#files

下载下来的文件是.tar.gz格式，在MacOS及Linux命令行中解压，指令：

将其中的lmfit文件夹复制到当前project目录下。

上述例子2中生成了data.dat，用来作为接下来的方法中的原始数据。

 出处：

Modeling Data and Curve Fitting

#Header
import numpy as np
import matplotlib.pyplot as plt
from numpy import exp, loadtxt, pi, sqrt
from lmfit import Model

#Import the data and define x, y and the function
data = loadtxt('data.dat')
x = data[0, :]
y = data[1, :]
def gaussian1(x, amp, cen, wid):
 return (amp / (sqrt(2*pi) * wid)) * exp(-(x-cen)**2 / (2*wid**2))

#Fitting
gmodel = Model(gaussian1)
result = gmodel.fit(y, x=x, amp=5, cen=5, wid=1) #Fit from initial values (5,5,1)
print(result.fit_report())

#Plot
plt.plot(x, y, 'bo',label='raw data')
plt.plot(x, result.init_fit, 'k--',label='init_fit')
plt.plot(x, result.best_fit, 'r-',label='best_fit')
#plt.show()

#Labels
plt.title("Gaussian Function Fitting")
plt.xlabel('x coordinate')
plt.ylabel('y coordinate')
plt.legend()
leg = plt.legend()  # remove the frame of Legend, personal choice
leg.get_frame().set_linewidth(0.0) # remove the frame of Legend, personal choice
#leg.get_frame().set_edgecolor('b') # change the color of Legend frame
#plt.show()

#Export figure
#plt.savefig('fit3.eps', format='eps', dpi=1000)
plt.savefig('fit3.pdf', format='pdf', dpi=1000, figsize=(8, 6), facecolor='w', edgecolor='k')
plt.savefig('fit3.jpg', format='jpg', dpi=1000, figsize=(8, 6), facecolor='w', edgecolor='k')

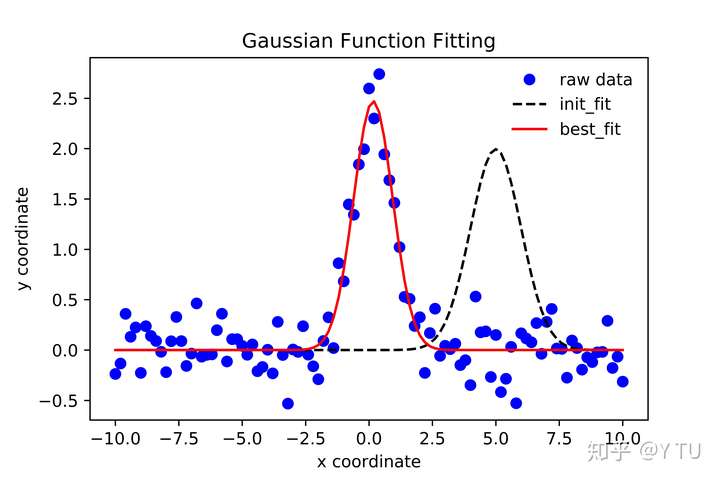
上面这一段代码需要按指示下载lmfit包，并且读取例子2中生成的data.dat。

得到的JPG导出图如下：

到此这篇关于利用python做数据拟合详情的文章就介绍到这了,更多相关python做数据拟合内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！