通过实例解析布隆过滤器工作原理及实例

布隆过滤器

布隆过滤器是一种数据结构，比较巧妙的概率型数据结构（probabilistic data structure），特点是高效地插入和查询，可以用来告诉你 “一定不存在或者可能存在”。

相比于传统的 List、Set、Map 等数据结构，它更高效、占用空间更少，但是缺点是其返回的结果是概率性的，而不是确切的。

布隆过滤器的工作原理

假设一个长度为m的bit类型的数组，即数组中每个位置只占一个bit，每个bit只有两种状态：0，1，所有bit的初始状态都为0。

再假设一共有k个哈希函数，这些函数的输出域大于或者等于m，并且这些哈希函数，彼此之间相互独立，每个哈希函数计算出来的结果是独立的，可能相同也可能不相同，对每一个计算出来的结果都对m取余（%m），然后再将数组下标位置置为1。

我们这里假设m为13,k为3的布隆过滤器，来看看布隆过滤器的工作原理：

当我们要映射一个值到布隆过滤器时，首先计算三个哈希函数的值，然后对13取余，映射到对应位中，图中映射到2，6，10，这样我们就完成了一个值的映射。

那么怎么判断一个值是否存在，当一个值输入时，通过三个哈希函数，然后取余，我们就可以得到对应的三个位置，我们只需要判断这三个位置是否都为1，如果都为1，则该值存储，反之不存在。

但是有一个特殊情况，前面说了不同的哈希函数可能计算可能相同也可能不相同，而且不同的哈希函数对不同的值计算出来的值可能一样，这就造成一个结果，一个值通过哈希和取余得到的位置，早就被其它值给置1了，当我们存储的值过多，而这个bit数组过小，都会造成这种情况更多的发生，一个值明明不存在，而它的所有位置早就被其它不同值置1，造成了误判，这里就对布隆过滤器提出了一个指标：失误率p。

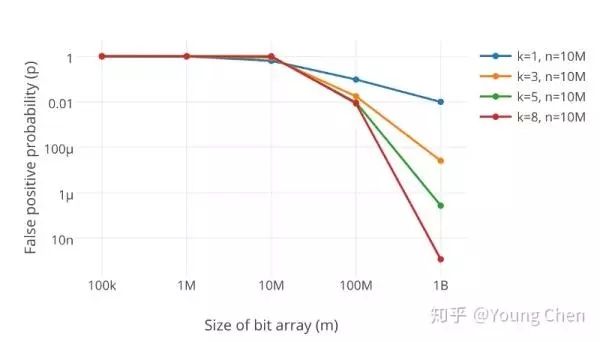
在同样数据规模下，不同大小的bit数组及不同数量k的哈希函数对误判率的结果：

如何选取最合适的m（bit数组的大小）及k（哈希函数的数量），在已知n（需要映射的值得数量）及失误率p的情况下：

m的选取：

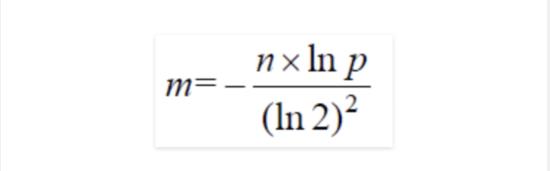
k的选取：

给个例子：假设n=100亿，p=0.01%

通过公式计算出来m=19.19n，向上取整位20n，即2000亿个bit，也就是25gb。

通过公式计算出来k=14。

计算真实失误率：

根据公式计算出来的真实失误率位0.006%。

c语言实现

#include <stdio.h>

#define Size 100
#define BitSIZE Size * 4 * 8
//c语言中一个整型数据类型4个字节
int bit[Size]={0};

int SDBMHash(char *str)
{
  unsigned int hash = 0;
  while (*str)
  {
    // equivalent to: hash = 65599*hash + (*str++);
    hash = (*str++) + (hash << 6) + (hash << 16) - hash;
  }
  return (hash & 0x7FFFFFFF);
}

int RSHash(char *str)
{
  unsigned int b = 378551;
  unsigned int a = 63689;
  unsigned int hash = 0;

  while (*str)
  {
    hash = hash * a + (*str++);
    a *= b;
  }

  return (hash & 0x7FFFFFFF);
}

int JSHash(char *str)
{
  unsigned int hash = 1315423911;

  while (*str)
  {
    hash ^= ((hash << 5) + (*str++) + (hash >> 2));
  }

  return (hash & 0x7FFFFFFF);
}

void Insert(int hash){

  //int value = hash%BitSIZE; ([0-3200]范围的值)
  //int listindex = value / 32; (listindex为数组下标)
  //int bitindex = value % 32; (某位)

  int value = hash%BitSIZE;
  int listindex = value / 32;
  int bitindex = value % 32;
  int temp = bit[listindex];
  bit[listindex] = bit[listindex] & (1 << bitindex);
  bit[listindex] = bit[listindex] | temp;
}

int Serach(int hash){
  int value = hash%BitSIZE;
  int listindex = value / 32;
  int bitindex = value % 32;
  if (bit[listindex] | (1 << bitindex)){
    return 1;
  }
  return 0;
}

int main () {

  char str1[] = "abc123";

  //在布隆过滤器中插入某值
  Insert(SDBMHash(str1));
  Insert(RSHash(str1));
  Insert(JSHash(str1));

  //在布隆过滤器中判断某值是否存在
  int i = 0;
  i = i+Serach(SDBMHash(str1));
  i = i+Serach(RSHash(str1));
  i = i+Serach(JSHash(str1));
  if(i == 3){
    printf("字符串：%s存在\n",str1);
  }

  return 0;
}

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持我们。

赞 (0)

相关推荐

  • python实现布隆过滤器及原理解析

    在学习redis过程中提到一个缓存击穿的问题, 书中参考的解决方案之一是使用布隆过滤器, 那么就有必要来了解一下什么是布隆过滤器.在参考了许多博客之后, 写个总结记录一下. 一.布隆过滤器简介 什么是布隆过滤器? 本质上布隆过滤器( BloomFilter )是一种数据结构,比较巧妙的概率型数据结构(probabilistic data structure),特点是高效地插入和查询,可以用来告诉你 "某样东西一定不存在或者可能存在". 相比于传统的 Set.Map 等数据结构,它更高效

  • 布隆过滤器的概述及Python实现方法

    布隆过滤器 布隆过滤器是一种概率空间高效的数据结构.它与hashmap非常相似,用于检索一个元素是否在一个集合中.它在检索元素是否存在时,能很好地取舍空间使用率与误报比例.正是由于这个特性,它被称作概率性数据结构(probabilistic data structure). 空间效率 我们来仔细地看看它的空间效率.如果你想在集合中存储一系列的元素,有很多种不同的做法.你可以把数据存储在hashmap,随后在hashmap中检索元素是否存在,hashmap的插入和查询的效率都非常高.但是,由于ha

  • JAVA实现较完善的布隆过滤器的示例代码

    布隆过滤器是可以用于判断一个元素是不是在一个集合里,并且相比于其它的数据结构,布隆过滤器在空间和时间方面都有巨大的优势.布隆过滤器存储空间和插入/查询时间都是常数.但是它也是拥有一定的缺点:布隆过滤器是有一定的误识别率以及删除困难的.本文中给出的布隆过滤器的实现,基本满足了日常使用所需要的功能. 0 0 0 0 0 0 0 0 0 0 先简单来说一下布隆过滤器.其实现方法就是:利用内存中一个长度为M的位数组B并初始化里面的所有位都为0,如下面的表格所示: 然后我们根据H个不同的散列函数,对传进来

  • C++ 数据结构之布隆过滤器

    布隆过滤器 一.历史背景知识 布隆过滤器(Bloom Filter)是1970年由布隆提出的.它实际上是一个很长的二进制向量和一系列随机映射函数.布隆过滤器可以用于检索一个元素是否在一个集合中.它的优点是空间效率和查询时间都远超过一般的算法,缺点是有一定的误识别率和删除错误.而这个缺点是不可避免的.但是绝对不会出现识别错误的情况出现(即假反例False negatives,如果某个元素确实没有在该集合中,那么Bloom Filter 是不会报告该元素存在集合中的,所以不会漏报) 在 FBI,一个

  • Python+Redis实现布隆过滤器

    布隆过滤器是什么 布隆过滤器(Bloom Filter)是1970年由布隆提出的.它实际上是一个很长的二进制向量和一系列随机映射函数.布隆过滤器可以用于检索一个元素是否在一个集合中.它的优点是空间效率和查询时间都比一般的算法要好的多,缺点是有一定的误识别率和删除困难. 布隆过滤器的基本思想 通过一种叫作散列表(又叫哈希表,Hash table)的数据结构.它可以通过一个Hash函数将一个元素映射成一个位阵列(Bit array)中的一个点.这样一来,我们只要看看这个点是不是1就可以知道集合中有没

  • Java实现布隆过滤器的方法步骤

    Java实现布隆过滤器的方法步骤

    前言 记得前段时间的文章么?redis使用位图法记录在线用户的状态,还是需要自己实现一个IM在线用户状态的记录,今天来讲讲另一方案,布隆过滤器 布隆过滤器的作用是加快判定一个元素是否在集合中出现的方法.因为其主要是过滤掉了大部分元素间的精确匹配,故称为过滤器. 布隆过滤器 在日常生活工作,我们会经常遇到这的场景,从一个Excel里面检索一个信息在不在Excel表中,还记得被CTRL+F支配的恐惧么,不扯了,软件开发中,一般会使用散列表来实现,Hash Table也叫哈希表,哈希表的优点是快速准确

  • 布隆过滤器(Bloom Filter)的Java实现方法

    布隆过滤器原理很简单:就是把一个字符串哈希成一个整数key,然后选取一个很长的比特序列,开始都是0,在key把此位置的0变为1:下次进来一个字符串,哈希之后的值key,如果在此比特位上的值也是1,那么就说明这个字符串存在了. 如果按照上面的做法,那就和哈希算法没有什么区别了,哈希算法还有重复的呢. 布隆过滤器是将一个字符串哈希成多个key,我还是按照书上的说吧. 先建立一个16亿二进制常量,然后将这16亿个二进制位全部置0.对于每个字符串,用8个不同的随机产生器(F1,F2,.....,F8)产

  • Redis 中的布隆过滤器的实现

    什么是『布隆过滤器』 布隆过滤器是一个神奇的数据结构,可以用来判断一个元素是否在一个集合中.很常用的一个功能是用来去重.在爬虫中常见的一个需求:目标网站 URL 千千万,怎么判断某个 URL 爬虫是否宠幸过?简单点可以爬虫每采集过一个 URL,就把这个 URL 存入数据库中,每次一个新的 URL 过来就到数据库查询下是否访问过. select id from table where url = 'https://jaychen.cc' 但是随着爬虫爬过的 URL 越来越多,每次请求前都要访问数据

  • 通过实例解析布隆过滤器工作原理及实例

    布隆过滤器 布隆过滤器是一种数据结构,比较巧妙的概率型数据结构(probabilistic data structure),特点是高效地插入和查询,可以用来告诉你 "一定不存在或者可能存在". 相比于传统的 List.Set.Map 等数据结构,它更高效.占用空间更少,但是缺点是其返回的结果是概率性的,而不是确切的. 布隆过滤器的工作原理 假设一个长度为m的bit类型的数组,即数组中每个位置只占一个bit,每个bit只有两种状态:0,1,所有bit的初始状态都为0. 再假设一共有k个哈

  • 通过代码实例解析PHP session工作原理

    这里的介绍主要是基于php语言,其他的语言操作可能会有差别,但基本的原理不变. 1.在php中如何操作session: session_start(); //使用该函数打开session功能 $_SESSION //使用预定义全局变量操作数据 使用unset($_SESSION['key']) //销毁一个session的值 简单地操作,一切都是由服务器实现:由于处理在后台,一切看起来也很安全.但是session采用什么样机制,又是怎样被实现,并且如何来保持会话的状态的呢? 2.session实

  • 通过实例解析python描述符原理作用

    这篇文章主要介绍了通过实例解析python描述符原理作用,文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习价值,需要的朋友可以参考下 本质上看,描述符是一个类,只不过它定义了另一个类中属性的访问方式.换句话说,一个类可以将属性管理全权委托给描述符类. 描述符类基于以下三种特殊方法,换句话说,这三种方法组成了描述符协议: __set__(self, obj, type = None): 在设置属性时,将调用这一方法. __get__(self, obj, value): 在读

  • 图文解析布隆过滤器大小的算法公式

    图文解析布隆过滤器大小的算法公式

    目录 1. 简介 2. 应用场景 2.1 缓存穿透 2.2 判断某个数据是否在海量数据中存在 3. HashMap的问题 4. 理解布隆过滤器 5. 根据布隆过滤器查询元素 6. 可以删除么 7. 如何选择哈希函数个数和布隆过滤器长度 更多应用场景 1. 简介 客户端:这个key存在吗? 服务器:不存在/不知道 本质上,布隆过滤器是一种数据结构,是一种比较巧妙的概率型数据结构.它的特点是高效地插入和查询.但我们要检查一个key是否在某个结构中存在时,通过使用布隆过滤器,我们可以快速了解到「这个k

  • 布隆过滤器的原理以及java 简单实现

    一.布隆过滤器 布隆过滤器(Bloom Filter)是1970年由布隆提出的.它实际上是一个很长的二进制向量和一系列随机映射函数.布隆过滤器可以用于检索一个元素是否在一个集合中.它的优点是空间效率和查询时间都远远超过一般的算法,缺点是有一定的误识别率和删除困难. 如果想判断一个元素是不是在一个集合里,一般想到的是将集合中所有元素保存起来,然后通过比较确定.链表.树.散列表(又叫哈希表,Hash table)等等数据结构都是这种思路.但是随着集合中元素的增加,我们需要的存储空间越来越大.同时检索

  • ASP.NET Core MVC中过滤器工作原理介绍

    ASP.NET Core MVC中过滤器工作原理介绍

    过滤器的作用是在 Action 方法执行前或执行后做一些加工处理.使用过滤器可以避免Action方法的重复代码,例如,您可以使用异常过滤器合并异常处理的代码. 过滤器如何工作? 过滤器在 MVC Action 调用管道中运行,有时称为过滤器管道.MVC选择要执行的Action方法后,才会执行过滤器管道: 实现 过滤器同时支持同步和异步两种不同的接口定义.您可以根据执行的任务类型,选择同步或异步实现. 同步过滤器定义OnStageExecuting和OnStageExecuted方法,会在管道特定

  • Java布隆过滤器的原理和实现分析

    目录 前言 1. 预备知识 1.1 哈希函数 2. 布隆过滤器 2.1 概念 2.2 实现原理 2.3 步骤 2.4 实现 前言 数组.链表.树等数据结构会存储元素的内容,一旦数据量过大,消耗的内存也会呈现线性增长 所以布隆过滤器是为了解决数据量大的一种数据结构 讲述布隆过滤器的时候需要了解一些预备的知识点:比如哈希函数 1. 预备知识 1.1 哈希函数 哈希函数指将哈希表中元素的关键键值映射为元素存储位置的函数 一般的线性表,树中,记录在结构中的相对位置是随机的,即和记录的关键字之间不存在确定

  • 实例分析浏览器中“JavaScript解析器”的工作原理

    浏览器在读取HTML文件的时候,只有当遇到<script>标签的时候,才会唤醒所谓的"JavaScript解析器"开始工作. JavaScript解析器工作步骤: 1."找一些东西": var. function. 参数:(也被称之为预解析) 备注:如果遇到重名分为以下两种情况: 遇到变量和函数重名了,只留下函数 遇到函数重名了,根据代码的上下文顺序,留下最后一个 2.逐行解读代码. 备注:表达式可以修改预解析的值 JS解析器在执行第一步预解析的时候,会

  • Linux NFS机制工作原理及实例解析

    什么是NFS? network file system 网络文件系统 通过网络存储和组织文件的一种方法或机制. 为什么要用NFS? 前端所有的应用服务器接收到用户上传的图片.文件.视频,都会统一放到后端的存储上. 共享存储的好处:方便数据的查找与取出,缺点:存储服务器压力大,坏了丢失全部数据. NFS工作原理 NFS功能,有很多服务,每个服务都有自己的端口,并且经常变换. 客户端查找这些端口,就需要一个中间人---RPC服务(默认端口号111). 工作流程: 1.启动RPC服务 2.启动NFS服

随机推荐