java数据结构算法稀疏数组示例详解

目录

• 一、什么是稀疏数组
• 二、场景用法
• 1.二维数组转稀疏数组思路
• 2.稀疏数组转二维数组思路
• 3.代码实现

一、什么是稀疏数组

当一个数组a中大部分元素为0，或者为同一个值，那么可以用稀疏数组b来保存数组a。

首先，稀疏数组是一个数组，然后以一种特定的方式来保存上述的数组a，具体处理方法：

• 记录数组a一共有几行几列
• 记录a中有多少个不同的值
• 最后记录不同值的元素所在行列，以及具体的值，放在一个小规模的数组里，以缩小程序的规模。

这个小规模的数组，就是稀疏数组。

举个栗子，左侧是一个二维数组，一共5行4列，其中非0的值一共有6个。于是，按照规则就可以转化成右侧的稀疏数组。

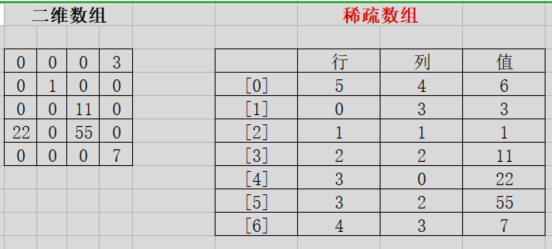
二、场景用法

意思听明白了，但是这玩意有啥应用场景呢？
比如现在有一个五子棋游戏的程序需求：游戏可以进行存盘，下次打开游戏可以续上盘。

那么记录五子棋的棋盘内容，其实用二维数组记录非常的直观。

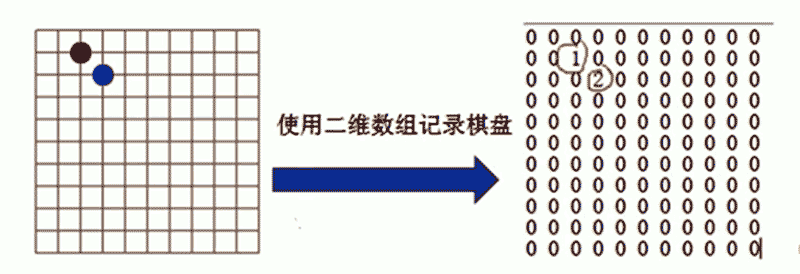
但是因为这个二维数组的很多值都是0，没有意义，所以可以考虑用稀疏数组对其进行转化。

1.二维数组转稀疏数组思路

如何转化，思路很简单：

• 遍历原始二维数组，得到有效数据的个数sum
• 根据sum就可以创建稀疏数组 sparseArr
• 将二维数组的有效数据存入到稀疏数组

2.稀疏数组转二维数组思路

读盘的时候需要把稀疏再转回二维数组：

• 先读取稀疏数组的第一行，根据第一行的数据，创建二维数组
• 继续读取稀疏数组后几行的数据，对二维数组赋值。

3.代码实现

过程很简单，对了，稀疏数组最好存到磁盘里(代码中不包含)，然后要用的时候再去读取转化回二维数组。

public class SparseArray {
    public static void main(String[] args) {
        // 创建原始二维数组，11*11
        // 0表示没有棋子，1表示黑子，2表示蓝子
        int chessArr1[][] = new int[11][11];
        chessArr1[1][2] = 1;
        chessArr1[2][3] = 2;
        // 输出原始的二维数组
        for (int[] row : chessArr1) {
            for (int data : row) {
                System.out.printf("%d\t", data);
            }
            System.out.println();
        }
        // 将二维数组 转化为 稀疏数组
        // 1. 先遍历二维数组，得到非0数据的个数
        int sum = 0;
        for (int i = 0; i < chessArr1.length; i++) {
            for (int j = 0; j < chessArr1.length ; j++) {
                if (chessArr1[i][j] != 0) {
                    sum++;
                }
            }
        }
        System.out.println("sum: " + sum);
        // 2. 创建对应的稀疏数组
        int sparseArr[][] = new int[sum+1][3];
        // 给稀疏数组赋值
        sparseArr[0][0] = 11;
        sparseArr[0][1] = 11;
        sparseArr[0][2] = sum;
        // 3. 遍历二维数组，得到非0数据存放到sparseArr
        int count = 0; // 用于记录是第几个非0数据
        for (int i = 0; i < chessArr1.length; i++) {
            for (int j = 0; j < chessArr1.length ; j++) {
                if (chessArr1[i][j] != 0) {
                    count++;
                    sparseArr[count][0] = i;
                    sparseArr[count][1] = j;
                    sparseArr[count][2] = chessArr1[i][j];
                }
            }
        }
        // 输出稀疏数组
        System.out.println("稀疏数组：");
        for (int i = 0; i <  sparseArr.length; i++) {
            System.out.printf("%d\t%d\t%d\t\n", sparseArr[i][0], sparseArr[i][1], sparseArr[i][2]);
        }
        System.out.println();
        // 将稀疏数组 恢复成 原始的 二维数组
        // 1. 先读取稀疏数组的第一行，根据第一行的数据，创建原始的二维数组
        int chessArr2[][] = new int[sparseArr[0][0]][sparseArr[0][1]];
        // 2. 读取稀疏数组的后几行数据，赋给原始的二维数组即可
        for (int i = 1; i < sparseArr.length; i++) {
            chessArr2[sparseArr[i][0]][sparseArr[i][1]] = sparseArr[i][2];
        }
        // 输出恢复后的二维数组
        System.out.println("恢复后的二维数组：");
        for (int[] row : chessArr2) {
            for (int data : row) {
                System.out.printf("%d\t", data);
            }
            System.out.println();
        }
    }
}

运行结果：

0	0	0	0	0	0	0	0	0	0	0
0	0	1	0	0	0	0	0	0	0	0
0	0	0	2	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0
sum: 2
稀疏数组：
11	11	2
1	2	1
2	3	2
恢复后的二维数组：
0	0	0	0	0	0	0	0	0	0	0
0	0	1	0	0	0	0	0	0	0	0
0	0	0	2	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	0	0
Process finished with exit code 0

以上就是java数据结构算法稀疏数组示例详解的详细内容，更多关于java数据结构算法稀疏数组的资料请关注我们其它相关文章！