Numpy数组的广播机制的实现

前言

Numpy数组不需要循环遍历，即可对每个元素执行批量的算术运算操作（矢量化运算）。当两个数组大小（Numpy.shape）不同时，进行算术运算会出现广播机制。

数组广播

数组在进行矢量化运算的时，要求数组形状时相等的。当形状不等的数组执行算术运算的时候，就会出现广播机制，该机制会对数组进行扩展，使数组的shape属性值一样，就可以进行矢量化运算了。

import numpy as np
arr1 = np.array([[0], [1], [2], [3]])
print(arr1.shape)
arr2 = np.array([1, 2, 3])
print(arr2.shape)
val = arr2+arr1
print(val)

输出结果
(4, 1) //arr1的shape
(3,) //arr2的shape
[[1 2 3]
[2 3 4]
[3 4 5]
[4 5 6]]

由于arr1和arr2的shape不等，故通过广播机制进行如下图的扩展

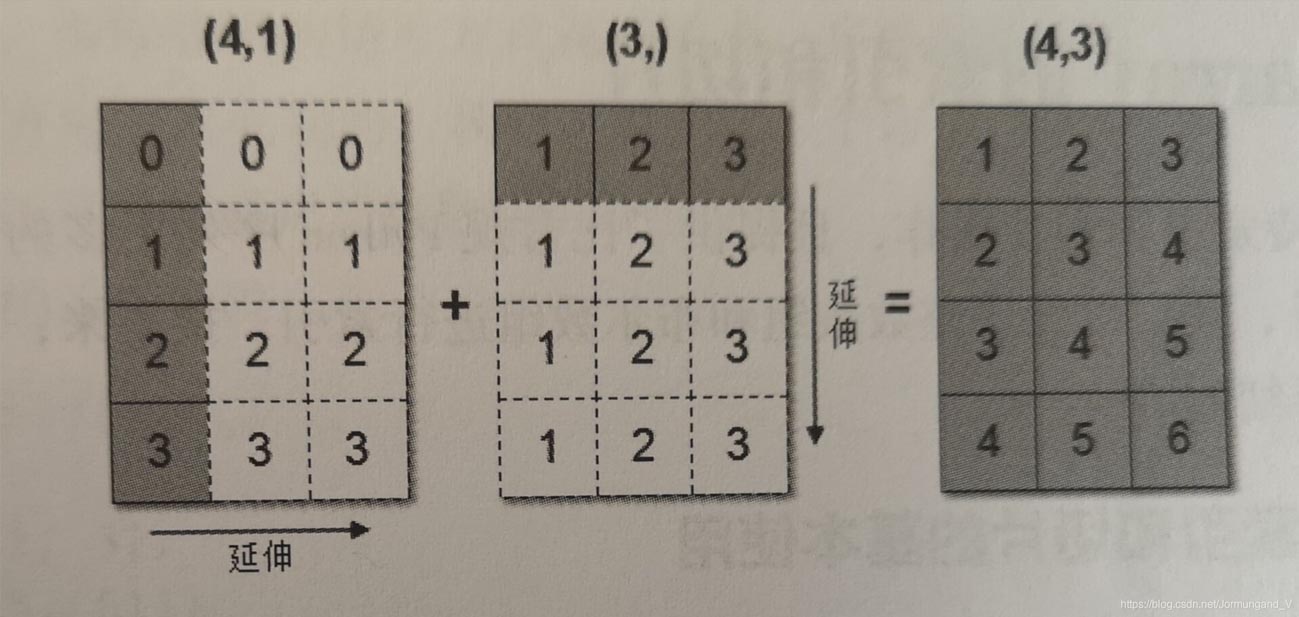
广播机制的使用条件

1、数组的某一维度等长
2、其中一个数组的某一维度为1

到此这篇关于Numpy数组的广播机制的实现的文章就介绍到这了,更多相关Numpy数组的广播机制内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！

赞 (0)

相关推荐

  • numpy数组广播的机制

    numpy数组的广播功能强大,但是也同时让人疑惑不解,现在让我们来谈谈其中的原理. 广播原则: 如果两个数组的后缘维度(即:从末尾开始算起的维度)的轴长相符或其中一方的长度为1,则认为它们是广播兼容的,广播会在缺失和(或)长度为1的轴上进行. 上面的原则很重要,是广播的指导思想,下面我们来看看例子. 1.其实在最简单的数组与标量数字之间的运算就存在广播,只是我们把它看作理所当然了. 2.再看下一个例子,这个大家都会一致认为这是广播了 根据广播原则:arr1的shape为(4,1),arr2的sh

  • 详解Numpy中的广播原则/机制

    广播的原则 如果两个数组的后缘维度(从末尾开始算起的维度)的轴长度相符或其中一方的长度为1,则认为它们是广播兼容的.广播会在缺失维度和(或)轴长度为1的维度上进行. 在上面的对arr每一列减去列平均值的例子中,arr的后缘维度为3,arr.mean(0)后缘维度也是3,满足轴长度相符的条件,广播会在缺失维度进行. 这里有点奇怪的是缺失维度不是axis=1,而是axis=0,个人理解是缺失维度指的是两个arr除了轴长度匹配的维度,在上面的例子中,正好是axis=0.这块欢迎指正 arr.mean(

  • Numpy数组的广播机制的实现

    前言 Numpy数组不需要循环遍历,即可对每个元素执行批量的算术运算操作(矢量化运算).当两个数组大小(Numpy.shape)不同时,进行算术运算会出现广播机制. 数组广播 数组在进行矢量化运算的时,要求数组形状时相等的.当形状不等的数组执行算术运算的时候,就会出现广播机制,该机制会对数组进行扩展,使数组的shape属性值一样,就可以进行矢量化运算了. import numpy as np arr1 = np.array([[0], [1], [2], [3]]) print(arr1.sha

  • 深入解析NumPy中的Broadcasting广播机制

    深入解析NumPy中的Broadcasting广播机制

    前言 在吴恩达老师的深度学习专项课程中,老师有提到NumPy中的广播机制,同时那一周的测验也有涉及到广播机制的题目.那么,到底什么是NumPy中的广播机制? 官方文档 接下来到了看官方文档的时间. Array Broadcasting in Numpy 广播机制概述 让我们探索numpy中一个更高级的概念,这个概念被称为广播. 广播展现了NumPy在算术运算期间是如何处理具有不同形状的数组的. 受到某些约束,较小的阵列将在较大的阵列上"广播",以使它们具有相同形状. 广播提供了一种数组

  • Broadcast广播机制在Pytorch Tensor Numpy中的使用详解

    目录 1.什么是广播机制 2.广播机制的规则 3.代码举例 4.原地操作 1.什么是广播机制 根据线性代数的运算规则我们知道,矩阵运算往往都是在两个矩阵维度相同或者相匹配时才能运算.比如加减法需要两个矩阵的维度相同,乘法需要前一个矩阵的列数与后一个矩阵的行数相等.那么在 numpy.tensor 里也是同样的道理,但是在机器学习的某些算法中会出现两个维度不相同也不匹配的矩阵进行运算,那么这时候就需要用广播机制来解决,通过广播机制,其tensor参数可以自动扩展为相等大小(不需要复制数据).下面我

  • Numpy数组的组合与分割实现的方法

    目录 数组的组合 1.水平组合 2.垂直组合 3.行组合和列组合 4.深度组合 数组的分割 1.水平分割 1.1hsplit函数 1.2split函数 2.垂直分割 3.深度分割 在介绍数组的组合和分割前,我们需要先了解数组的维(ndim)和轴(axis)概念. 如果数组的元素是数组,即数组嵌套数组,我们就称其为多维数组.几层嵌套就称几维.比如形状为(a,b)的二维数组就可以看作两个一维数组,第一个一维数组包含a个一维数组,第二个一维数组包含b个数据. 每一个一维线性数组称为一个轴.二维数组的第

  • Python如何遍历numpy数组

    目录 Python遍历numpy数组 numpy中数组的遍历技巧分享 1. 内置for循环 2. flat迭代器 3. nditer迭代器 Python遍历numpy数组 下面是示例代码: import numpy as np num = np.zeros([2, 3]) [rows, cols] = num.shape print(rows, cols) for i in range(rows):     for j in range(cols):         print(num[i, j

  • Numpy 数组索引的实现

    目录 一.整数索引 二.切片索引 2.1.一维数组切片 三.整数数组索引 3.1. 一维数组的整数数组索引 3.2.多维数组的整数数组索引 四.布尔索引 五.花式索引 数组索引是指使用方括号([])来索引数组值,numpy提供了比常规的python序列更多的索引工具.除了按整数和切片索引之外,数组可以由整数数组索引.布尔索引及花式索引.下面逐一学习. 一.整数索引 这种机制有助于基于 N 维索引来获取数组中任意元素. 每个整数数组表示该维度的下标值. 当索引的元素个数就是目标ndarray的维度

  • 对numpy 数组和矩阵的乘法的进一步理解

    1.当为array的时候,默认d*f就是对应元素的乘积,multiply也是对应元素的乘积,dot(d,f)会转化为矩阵的乘积, dot点乘意味着相加,而multiply只是对应元素相乘,不相加 2.当为mat的时候,默认d*f就是矩阵的乘积,multiply转化为对应元素的乘积,dot(d,f)为矩阵的乘积 3. 混合时候的情况,一般不要混合 混合的时候默认按照矩阵乘法的, multiply转化为对应元素的乘积,dot(d,f)为矩阵的乘积 总结:数组乘法默认的是点乘,矩阵默认的是矩阵乘法,混

  • Python中numpy数组的计算与转置详解

    Python中numpy数组的计算与转置详解

    目录 前言 1.numpy数组与数的运算 2.numpy相同尺寸的数组运算 3.numpy不同尺寸的数组计算 4.numpy数组的转置 总结: 前言 本文主要讲述numpy数组的计算与转置,讲相同尺寸数组的运算与不同尺寸数组的运算,同时介绍数组转置的三种方法. numpy数组的操作比较枯燥,但是都很实用,在很多机器学习.深度学习算法中都会使用到,对numpy数组的一些操作. 1.numpy数组与数的运算 主要包括数组与数的加减乘除运算,废话不多说,看代码: import numpy as np

  • python的广播机制详解

    python的广播机制详解

    目录 为什么会有广播机制 在矩阵或向量相关运算中的广播机制 1.一般的运算 2.一个矩阵一个向量的情况 3.两个向量 4.矩阵乘法的广播机制 总结 为什么会有广播机制 python语言在设计的时候,就就考虑到用于两个运算的矩阵或向量维度不匹配的问题.例如,我们有矩阵A,让矩阵每个元素都加1,直接使用A+1,就可以完成目的.这其中就用到了python的广播机制,所以在很多python的第三方库中,都支持广播机制,例如Numpy.pytorch. 在矩阵或向量相关运算中的广播机制 1.一般的运算 假

随机推荐