python3实现二叉树的遍历与递归算法解析(小结)

1、二叉树的三种遍历方式

二叉树有三种遍历方式：先序遍历，中序遍历，后续遍历 即：先中后指的是访问根节点的顺序 eg:先序 根左右 中序 左根右 后序 左右根

遍历总体思路：将树分成最小的子树，然后按照顺序输出

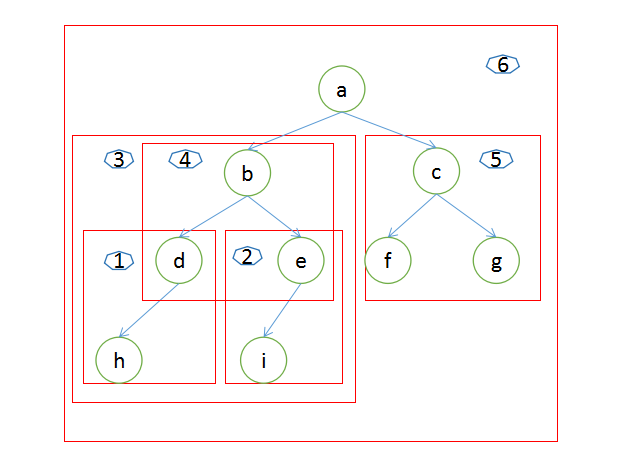
1.1 先序遍历

　　　　a 先访问根节点

　　　　b 访问左节点

　　　　c 访问右节点

　　　　a（b ( d ( h ) )( e ( i ) )）( c ( f )( g )) -- abdheicfg

1.2 中序遍历

　　　　a 先访问左节点

　　　　b 访问根节点

　　　　c 访问右节点

　　　　( ( ( h ) d ) b ( ( i ) e ) ) a ( ( f ) c ( g ) ) -- hdbieafcg

1.3后序遍历

　　　　a 先访问左节点

　　　　b 访问右节点

　　　　c 访问根节点

　　　　((hd)(ie)b)(fgc)a -- hdiebfgca

2、python3实现树结构

#实现树结构的类，树的节点有三个私有属性 左指针 右指针 自身的值
class Node():

  def __init__(self,data=None):
    self._data = data
    self._left = None
    self._right = None

  def set_data(self,data):
    self._data = data

  def get_data(self):
    return self._data

  def set_left(self,node):
    self._left = node

  def get_left(self):
    return self._left

  def set_right(self,node):
    self._right = node

  def get_right(self):
    return self._right

if __name__ == '__main__':
  #实例化根节点
  root_node = Node('a')
  # root_node.set_data('a')
  #实例化左子节点
  left_node = Node('b')
  #实例化右子节点
  right_node = Node('c')

  #给根节点的左指针赋值，使其指向左子节点
  root_node.set_left(left_node)
  #给根节点的右指针赋值，使其指向右子节点
  root_node.set_right(right_node)

  print(root_node.get_data(),root_node.get_left().get_data(),root_node.get_right().get_data())

3、实现树的递归遍历（前 中 后 层次遍历）

下例是树的遍历算法，其中对树的类进行了优化，

#实现树结构的类，树的节点有三个私有属性 左指针 右指针 自己的值
class Node():

  def __init__(self,data =None,left=None,right = None):
    self._data = data
    self._left = left
    self._right = right

#先序遍历 遍历过程 根左右
def pro_order(tree):
  if tree == None:
    return False
  print(tree._data)
  pro_order(tree._left)
  pro_order(tree._right)

#后序遍历
def pos_order(tree):
  if tree == None:
    return False
  # print(tree.get_data())
  pos_order(tree._left)
  pos_order(tree._right)
  print(tree._data)

#中序遍历
def mid_order(tree):
  if tree == None:
    return False
  # print(tree.get_data())
  mid_order(tree._left)
  print(tree._data)
  mid_order(tree._right)

#层次遍历
def row_order(tree):
  # print(tree._data)
  queue = []
  queue.append(tree)
  while True:
    if queue==[]:
      break
    print(queue[0]._data)
    first_tree = queue[0]
    if first_tree._left != None:
      queue.append(first_tree._left)
    if first_tree._right != None:
      queue.append(first_tree._right)
    queue.remove(first_tree)

if __name__ == '__main__':

  tree = Node('A',Node('B',Node('D'),Node('E')),Node('C',Node('F'),Node('G')))
  pro_order(tree)
  mid_order(tree)
  pos_order(tree)

4、递归算法

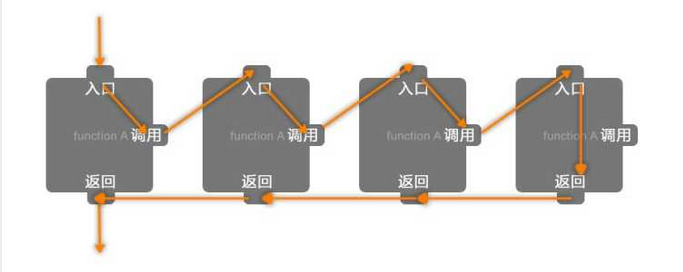
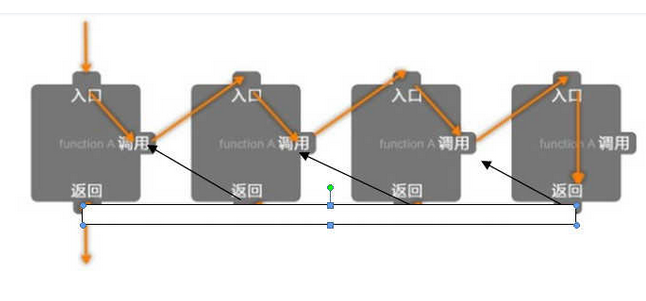
上面两张图片是从知乎贴过来的；图1中返回后会直接返回到上一级的返回，这种想法是不全面的，较合理的返回应该是如图2 在子函数返回时应返回到调用子函数的节点，这样在执行完剩余代码再返回到上一级

如果是按照图1返回的话二叉树的遍历就不能按照上例来实现。

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持我们。