C语言算法金手指摩尔投票法手撕绝大多数问题

目录

• 正片开始
• 概念
• 优点
• 算法核心
• 实现

正片开始

概念

嘛是摩尔投票法？
简单来说就是投票法，算法解决的问题是如何在任意多的候选人，选出获得票数最多的那个。常见的算法是扫描一遍选票，也就是遍历，对每个候选人进行统计的选票进行统计。

那我遍历难道不香吗？

这里就要讲一下投票法的过人之处

优点

当执行有序情况时，只要找到中位数，然后检查中位数的个数是否超过选票的一半即可。但是当对象的数目不定时，统计选票可能会执行较长时间，相比原来的时间复杂度 O(n) ，可能需运行 O(n^2) 的时间。

针对无序且对象不定的情况，摩尔投票法应运而生。

算法核心

摩尔投票法的关键就是抵消和计数，抵消过程类似于是在进行投票，然后计数我们可以脑补一个情形：当三人中的一人得票数远超其他两人时，我们就可以进行等量对消，消完还有票的自然就是得票数最多的那个，模拟如下：（ppt手残勿喷）

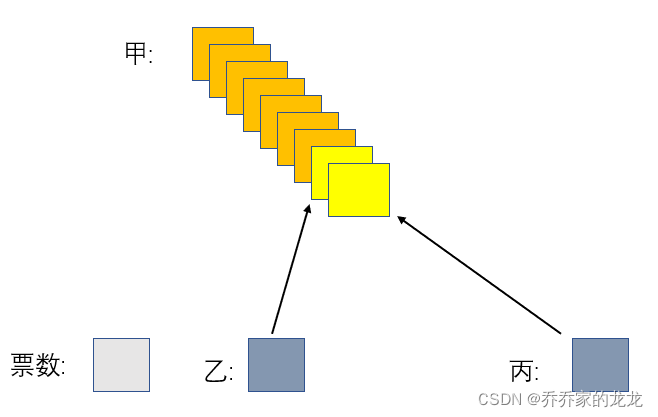
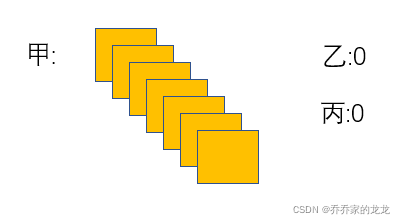
实现

基本思路就是由一个计数器维护，在进行比较过程中，不同票消掉，相同票保留，如果消的没有了就直接放进去然后继续上述过程，直到维护对象只剩一个，就是我们要找的最大得票者（众数）。

基于LeetCode真题实践，先看一个初级栗子：

169. 多数元素
给定一个大小为 n 的数组，找到其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。你可以假设数组是非空的，并且给定的数组总是存在多数元素。

示例：
输入：[2,2,1,1,1,2,2]
输出：2

来源：力扣（LeetCode）

我最初的思路是哈希思想，qsort 之后用最大的元素 malloc 一块新的空间，桶排后用 count 进行++，最后输出 count 最大的。有点麻烦而且我忽视了一个最大的问题就是负数的存在，垮掉~

根据我们算法的思路，针对目标数组 nums，首先创建一个变量来执行计数器 count 再创建一个新数组 a 进行比对，因为始终是目标数组的内部元素比较，我可以直接把 nums 首元素赋给 a ，比较时从第二个元素开始和 a 比较，如果相同，count ++；不同消掉，count --；没有了就往里拿。

int majorityElement(int* nums, int numsSize){
    int count = 1;
    int a = nums[0];
    for(int i =1;i<numsSize;i++)
    {
        if(nums[i]==a)
        {
            count++;
        }
        else
        {
            count--;
        }
        if(count==0)
        {
        a = nums[i+1];
        }
    }
    return a;
}

格局抬高

现在整一道硬菜，直接上升级版：
229. 求众数 II
给定一个大小为 n 的整数数组，找出其中所有出现超过 ⌊ n/3 ⌋ 次的元素。

示例 ：
输入：[1,1,1,3,3,2,2,2]
输出：[1,2]

还是那句话，题目越少眼泪越饱，短小精悍的题 nnd 硬磨了我一个下午，桶是肯定桶不了的，哈希又没学，不做吧心里太不舒服，这里就又有我摩尔投票法的一席之地了

注意，题目给的是超过 n/3 次的元素，这很重要，其实就是在暗示我们结果至多只会有三种情况：没有众数或者一个众数或者两个众数；但是头疼的是咱之前的摩尔投票法好像行不通，因为这里对象不定，如果出现了两个众数我的 “ 票 ” 该怎么投？

将之前的格局打开，我们可以将所有数字分为两类，> n/3 的元素 和 <= n/3 的元素,其中大于 n/3 的元素最多只有两个。因此可以设置三个变量，进行相对抵消，这里我们不妨再引入一个容器 b，再用一个新的计数器 count2 来进行维护，当三个元素相同时，count++，不同就抵消，为 0 就用把这个数放进去，基本思想和上面是差不多的：

    int a = nums[0];
	int b = nums[1];
	int count1, count2 = 0;
	for (int i = 0; i < numsSize; i++)
	{
		if (a == nums[i])
		{
			count1++;
			continue;
		}
		else if (b == nums[i])
		{
			count2++;
			continue;
		}
		else
		{
			count1--;
			count2--;
		}
		if (count1 < 0)
		{
			a = nums[i];
			count2++;
			count1 = 1;
		}
		if (count2 < 0)
		{
			b = nums[i];
			count1++;
			count2 = 1;
		}
	}

还没完，因为数组可能存在一个众数或者没有众数的情况，我们还需要再次遍历来统计我们筛选的众数的出现次数是否符合题目要求的大于n/3 以及排除数组为空或单项的情况：

    count1 = 0;
	count2 = 0;
	for (int i = 0; i < numsSize; i++)
	{
		if (a == nums[i])
		{
			count1++;
		}
	    else if (b == nums[i])
		{
			count2++;
		}
	}
		if (numsSize <= 1)
	{
		*returnSize = numsSize;
		return nums;
	}

最后直接依次放入一块新的空间再返回即可，全部代码如下：

int* majorityElement(int* nums, int numsSize, int* returnSize) {
	if (numsSize <= 1)
	{
		*returnSize = numsSize;
		return nums;
	}
	int a = nums[0];
	int b = nums[1];
	int count1, count2 = 0;
	for (int i = 0; i < numsSize; i++)
	{
		if (a == nums[i])
		{
			count1++;
			continue;
		}
		else if (b == nums[i])
		{
			count2++;
			continue;
		}
		else
		{
			count1--;
			count2--;
		}
		if (count1 < 0)
		{
			a = nums[i];
			count2++;
			count1 = 1;
		}
		if (count2 < 0)
		{
			b = nums[i];
			count1++;
			count2 = 1;
		}

	}
	count1 = 0;
	count2 = 0;
	for (int i = 0; i < numsSize; i++)
	{
		if (a == nums[i])
		{
			count1++;
		}
	    else if (b == nums[i])
		{
			count2++;
		}
	}
	int* c = (int*)malloc(sizeof(int) * 2);
    *returnSize = 0;
	if (count1 > numsSize / 3)
	{
		c[(*returnSize)++] = a;
	}
	if (count2 > numsSize / 3)
	{
		c[(*returnSize)++] = b;
	}
	return c;
}

家人们明白了吗，那今天就到这里，摸了。

以上就是C语言算法金手指摩尔投票法手撕绝大多数问题的详细内容，更多关于C语言摩尔投票算法的资料请关注我们其它相关文章！