Python 经典贪心算法之Prim算法案例详解

最小生成树的Prim算法也是贪心算法的一大经典应用。Prim算法的特点是时刻维护一棵树，算法不断加边，加的过程始终是一棵树。

Prim算法过程：
一条边一条边地加， 维护一棵树。

初始 E ＝ ｛｝空集合， V = ｛任选的一个起始节点｝
循环（n – 1）次，每次选择一条边（v1,v2）， 满足：v1属于V , v2不属于V。且（v1,v2）权值最小。
E = E + （v1,v2）
V = V + v2

最终E中的边是一棵最小生成树， V包含了全部节点。

以下图为例介绍Prim算法的执行过程。

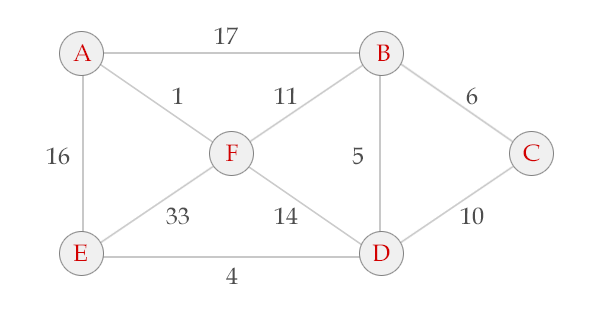
Prim算法的过程从A开始 V = {A}, E = {}

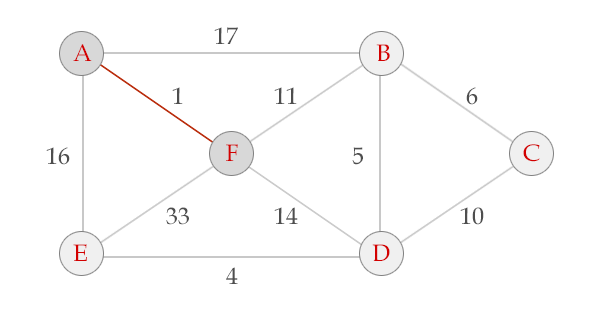
选中边AF , V = {A, F}, E = {(A,F)} 

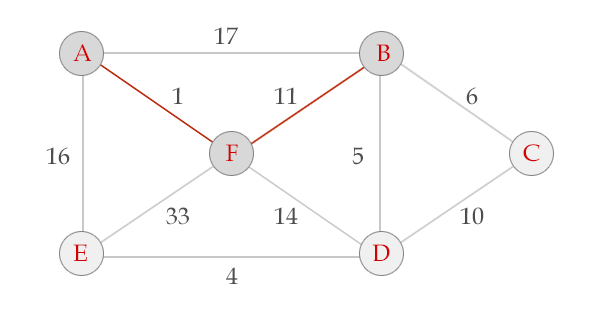
选中边FB, V = {A, F, B}, E = {(A,F), (F,B)}

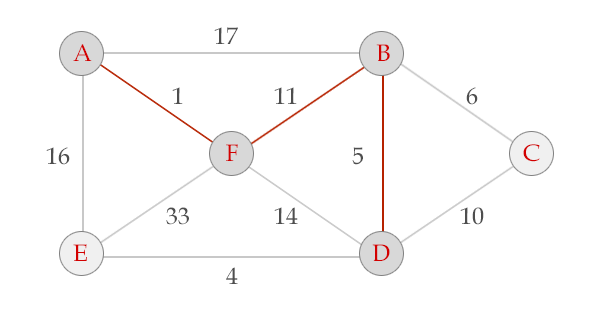
选中边BD, V = {A, B, F, D},   E = {(A,F), (F,B), (B,D)}

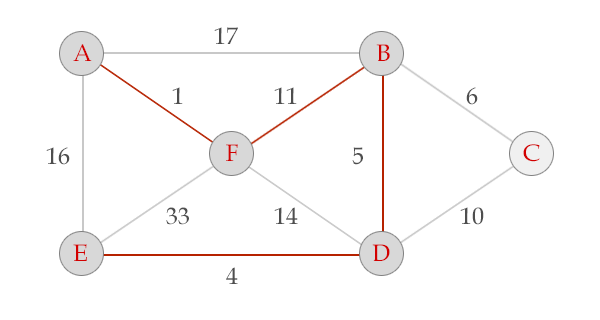
选中边DE, V = {A, B, F, D, E},   E = {(A,F), (F,B), (B,D), (D,E)}

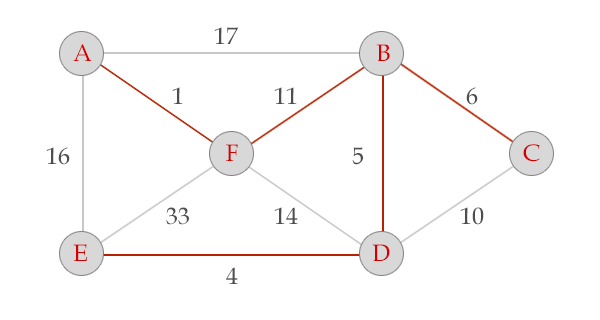
选中边BC, V = {A, B, F, D, E, c},   E = {(A,F), (F,B), (B,D), (D,E), (B,C)}, 算法结束。

Prim算法的证明：假设Prim算法得到一棵树P，有一棵最小生成树T。假设P和T不同，我们假设Prim算法进行到第(K – 1)步时选择的边都在T中，这时Prim算法的树是P', 第K步时,Prim算法选择了一条边e = (u, v)不在T中。假设u在P'中，而v不在。

因为T是树，所以T中必然有一条u到v的路径，我们考虑这条路径上第一个点u在P'中，最后一个点v不在P'中，则路径上一定有一条边f = (x,y)，x在P'中，而且y不在P'中。
我们考虑f和e的边权w(f)与w(e)的关系： 若w(f) > w(e)，在T中用e换掉f （T中加上e去掉f)，得到一个权值和更小的生成树，与T是最小生成树矛盾。
若w(f) < w(e), Prim算法在第K步时应该考虑加边f，而不是e,矛盾。

因此只有w(f) = w(e),我们在T中用e换掉f，这样Prim算法在前K步选择的边在T中了，有限步之后把T变成P,而树权值和不变， 从而Prim算法是正确的。
请仔细理解Prim算法——时刻维护一棵生成树。我们的证明构造性地证明了所有地最小生成树地边权（多重）集合都相同！

N个点M条边的无向连通图，每条边有一个权值，求该图的最小生成树。

最后，我们来提供输入输出数据，由你来写一段程序，实现这个算法，只有写出了正确的程序，才能继续后面的课程。

输入

第1行：2个数N,M中间用空格分隔，N为点的数量，M为边的数量。（2 <= N <= 1000, 1 <= M <= 50000)
第2 - M + 1行：每行3个数S E W，分别表示M条边的2个顶点及权值。(1 <= S, E <= N，1 <= W <= 10000)

输出

输出最小生成树的所有边的权值之和。

输入示例

9 14
1 2 4
2 3 8
3 4 7
4 5 9
5 6 10
6 7 2
7 8 1
8 9 7
2 8 11
3 9 2
7 9 6
3 6 4
4 6 14
1 8 8

输出示例

37

maxv=10001
n,m=list(map(int,input().split()))
E=[]
V=set([1])
cost=[]
for i in range(n+1):
    a=[]
    for j in range(n+1):
        a.append(maxv)
    cost.append(a)
for i in range(m):
    s,e,w=list(map(int,input().split()))
    cost[s][e]=w
    cost[e][s]=w
closet=[0]
lowcost=[maxv]
for i in range(1,n+1):
    closet.append(1)
    lowcost.append(cost[1][i])
ans=0
for i in range(n-1):
    k=0
    for j in range(2,n+1):
        if (lowcost[j]!=0) and (lowcost[j]<lowcost[k]):k=j

    for j in range(2,n+1):
        if cost[j][k]<lowcost[j]:
            lowcost[j]=cost[j][k]
            closet[j]=k
    ans+=lowcost[k]
    lowcost[k]=0
print(ans)

到此这篇关于Python 经典贪心算法之Prim算法案例详解的文章就介绍到这了,更多相关Python 经典贪心算法之Prim内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！

赞 (0)

相关推荐

  • Dijkstra算法与Prim算法的异同案例详解

    目录 Dijkstra简述 Prim简述 异 同 思想 时间复杂度 Dijkstra特例 Dijkstra简述 Dijkstra算法用于构建单源点的最短路径树(MST)--即树中某个点到任何其他点的距离都是最短的.例如,构建地图应用时查找自己的坐标离某个地标的最短距离.可以用于有向图,但是不能存在负权值(Bellman-Ford可以处理负权值). 伪代码 Dijkstra() { for each u in G,V { //此处做初始化操作,给每个节点u赋键值+∞,设置空为父节点 u.key =

  • python Dijkstra算法实现最短路径问题的方法

    本文借鉴于张广河教授主编的<数据结构>,对其中的代码进行了完善. 从某源点到其余各顶点的最短路径 Dijkstra算法可用于求解图中某源点到其余各顶点的最短路径.假设G={V,{E}}是含有n个顶点的有向图,以该图中顶点v为源点,使用Dijkstra算法求顶点v到图中其余各顶点的最短路径的基本思想如下: 使用集合S记录已求得最短路径的终点,初始时S={v}. 选择一条长度最小的最短路径,该路径的终点w属于V-S,将w并入S,并将该最短路径的长度记为Dw. 对于V-S中任一顶点是s,将源点到顶点

  • 详解Dijkstra算法之最短路径问题

    详解Dijkstra算法之最短路径问题

    一.最短路径问题介绍 问题解释: 从图中的某个顶点出发到达另外一个顶点的所经过的边的权重和最小的一条路径,称为最短路径 解决问题的算法: 迪杰斯特拉算法(Dijkstra算法) 弗洛伊德算法(Floyd算法) SPFA算法 这篇博客,我们就对Dijkstra算法来做一个详细的介绍 二.Dijkstra算法介绍 2.1.算法特点 迪科斯彻算法使用了广度优先搜索解决赋权有向图或者无向图的单源最短路径问题,算法最终得到一个最短路径树.该算法常用于路由算法或者作为其他图算法的一个子模块. 2.2.算法的

  • python实现Dijkstra算法的最短路径问题

    迪杰斯特拉(Dijkstra)算法主要是针对没有负值的有向图,求解其中的单一起点到其他顶点的最短路径算法. 1 算法原理 迪杰斯特拉(Dijkstra)算法是一个按照路径长度递增的次序产生的最短路径算法.下图为带权值的有向图,作为程序中的实验数据. 其中,带权值的有向图采用邻接矩阵graph来进行存储,在计算中就是采用n*n的二维数组来进行存储,v0-v5表示数组的索引编号0-5,二维数组的值表示节点之间的权值,若两个节点不能通行,比如,v0->v1不能通行,那么graph[0,1]=+∞ (采

  • c++ primer中的const限定符

    const 限定符  const是一种类型修饰符,用于说明永不改变的对象.const对象一旦定义,就无法再赋新值,所以必须被初始化. 例:const int bufsize = 512; 它的值一旦定义就不能被改变,并且默认情况下,仅对文件内有效. 如果要在多个文件中共享const对象,则需要在定义和声明前都加extern: 初始化和对const的引用 例: const int ci = 1024; const int &r1= ci; r1 = 42; // 值不可以被改变 int &r

  • MongoDB 主分片(primary shard)相关总结

    01 主分片是什么? 分片集群中的每一个数据库都有一个主分片,这个主分片上保存了当前数据库中没有被分片的集合的数据,主分片(primary shard)和主节点(primary)之间没有任何关联. 主分片是由mongos选择出来的,选择的依据是每当创建新数据库的时候,mongos会从集群中选择包含数据最少的分片作为新数据库的主分片.具体的选择方式是: 选择listDatabase命令返回的totalSize字段作为选择的准则.如下: mongos> db.adminCommand("lis

  • 实现Dijkstra算法最短路径问题详解

    实现Dijkstra算法最短路径问题详解

    1.最短路径问题介绍 问题解释: 从图中的某个顶点出发到达另外一个顶点的所经过的边的权重和最小的一条路径,称为最短路径 解决问题的算法: 迪杰斯特拉算法(Dijkstra算法) 弗洛伊德算法(Floyd算法) SPFA算法 这篇博客,我们就对Dijkstra算法来做一个详细的介绍 2.Dijkstra算法介绍 算法特点: 迪科斯彻算法使用了广度优先搜索解决赋权有向图或者无向图的单源最短路径问题,算法最终得到一个最短路径树.该算法常用于路由算法或者作为其他图算法的一个子模块. 算法的思路 Dijk

  • python中mpi4py的所有基础使用案例详解

    python中mpi4py的基础使用 大多数 MPI 程序都可以使用命令 mpiexec 运行.在实践中,运行 Python 程序如下所示: $ mpiexec -n 4 python script.py 案例1:测试comm.send 和comm.recv函数,代码如下 from mpi4py import MPI comm = MPI.COMM_WORLD rank = comm.Get_rank() if rank == 0:     data = {'a': 7, 'b': 3.14}

  • Python实现线程池工作模式的案例详解

    Python实现线程池工作模式的案例详解

    目录 01.客户机/服务器通信逻辑 02.数据交换协议 03.服务器主体逻辑 04.服务器会话线程 05.客户机主体逻辑 06.客户机发送数据 07.客户机接收数据 08.客户机界面设计 09.线程池 10.联合测试 11.小结 本文章基于苹果树病虫害预测模型,自定义应用层通信逻辑,设计服务器与客户机.客户机向服务器发送图像数据,服务器回送预测结果.为增强服务器的可靠性与可扩展性,服务器端采用线程池工作模式.为了增强客户机的可操作性,客户机采用PyQt5完成图形化界面设计. 01.客户机/服务器

  • Python 经典贪心算法之Prim算法案例详解

    Python 经典贪心算法之Prim算法案例详解

    最小生成树的Prim算法也是贪心算法的一大经典应用.Prim算法的特点是时刻维护一棵树,算法不断加边,加的过程始终是一棵树. Prim算法过程: 一条边一条边地加, 维护一棵树. 初始 E ＝ {}空集合, V = {任选的一个起始节点} 循环(n – 1)次,每次选择一条边(v1,v2), 满足:v1属于V , v2不属于V.且(v1,v2)权值最小. E = E + (v1,v2) V = V + v2 最终E中的边是一棵最小生成树, V包含了全部节点. 以下图为例介绍Prim算法的执行过程

  • JVM中四种GC算法案例详解

    JVM中四种GC算法案例详解

    目录 介绍 引用计数算法(Reference counting) 算法思想: 核心思想: 优点: 缺点: 例子如图: 标记–清除算法(Mark-Sweep) 算法思想: 优点 缺点 例子如图 标记–整理算法 算法思想 优点 缺点 例子 复制算法 算法思想 优点 缺点 总结 介绍 程序在运行过程中,会产生大量的内存垃圾(一些没有引用指向的内存对象都属于内存垃圾,因为这些对象已经无法访问,程序用不了它们了,对程序而言它们已经死亡),为了确保程序运行时的性能,java虚拟机在程序运行的过程中不断地进行

  • python人工智能算法之决策树流程示例详解

    目录 决策树 总结 决策树 是一种将数据集通过分割成小的.易于处理的子集来进行分类或回归的算法.其中每个节点代表一个用于划分数据的特征,每个叶子节点代表一个类别或一个预测值.构建决策树时,算法会选择最好的特征进行分割数据,使每个子集中的数据尽可能的归属同一类或具有相似的特征.这个过程会不断重复,类似于Java中的递归,直到达到停止条件(例如叶子节点数目达到一个预设值),形成一棵完整的决策树.它适合于处理分类和回归任务.而在人工智能领域,决策树也是一种经典的算法,具有广泛的应用. 接下来简单介绍下

  • Java DFA算法案例详解

    Java DFA算法案例详解

    1.背景 项目中需要对敏感词做一个过滤,首先有几个方案可以选择: 直接将敏感词组织成String后,利用indexOf方法来查询. 传统的敏感词入库后SQL查询. 利用Lucene建立分词索引来查询. 利用DFA算法来进行. 首先,项目收集到的敏感词有几千条,使用a方案肯定不行.其次,为了方便以后的扩展性尽量减少对数据库的依赖,所以放弃b方案.然后Lucene本身作为本地索引,敏感词增加后需要触发更新索引,并且这里本着轻量原则不想引入更多的库,所以放弃c方案.于是我们选定d方案为研究目标. 2.

  • C语言实现BF算法案例详解

    C语言实现BF算法案例详解

    BF算法:        BF算法即暴风算法,是普通的模式匹配算法.BF算法的思想:将目标串S的第一个字符与模式串T的第一个字符进行匹配,若相等,则继续比较S的第二个字符和 T的第二个字符:若不相等,则比较S的第二个字符和T的第一个字符,依次比较下去,直到得出最后的匹配结果.BF算法是一种蛮力算法. 图示: #include <stdio.h> #include <string.h> int BF(const char *s, const char* sub, int pos)//

  • python机器学习算法与数据降维分析详解

    python机器学习算法与数据降维分析详解

    目录 一.数据降维 1.特征选择 2.主成分分析(PCA) 3.降维方法使用流程 二.机器学习开发流程 1.机器学习算法分类 2.机器学习开发流程 三.转换器与估计器 1.转换器 2.估计器 一.数据降维 机器学习中的维度就是特征的数量,降维即减少特征数量.降维方式有:特征选择.主成分分析. 1.特征选择 当出现以下情况时,可选择该方式降维: ①冗余:部分特征的相关度高,容易消耗计算性能 ②噪声:部分特征对预测结果有影响 特征选择主要方法:过滤式(VarianceThreshold).嵌入式(正

  • python目标检测SSD算法预测部分源码详解

    python目标检测SSD算法预测部分源码详解

    目录 学习前言 什么是SSD算法 ssd_vgg_300主体的源码 学习前言 ……学习了很多有关目标检测的概念呀,咕噜咕噜,可是要怎么才能进行预测呢,我看了好久的SSD源码,将其中的预测部分提取了出来,训练部分我还没看懂 什么是SSD算法 SSD是一种非常优秀的one-stage方法,one-stage算法就是目标检测和分类是同时完成的,其主要思路是均匀地在图片的不同位置进行密集抽样,抽样时可以采用不同尺度和长宽比,然后利用CNN提取特征后直接进行分类与回归,整个过程只需要一步,所以其优势是速度

随机推荐