C语言非递归算法解决快速排序与归并排序产生的栈溢出

目录

• 1、栈溢出原因和递归的基本认识
• 2、快速排序（非递归实现）
• 3、归并排序（非递归实现）

建议还不理解快速排序和归并排序的小伙伴们可以先去看我上一篇博客​​​​​​哦！C语言超详细讲解排序算法下篇

1、栈溢出原因和递归的基本认识

我们先简单来了解下内存分布结构：

栈区：用于存放地址、临时变量等；                                                                           

堆区：程序运行期间动态分配所使用的场景；

静态区：存放全局变量和静态变量，具体还分为 .bss段和.data段；

               .bss段：存放未初始化的和初始化为0的全局变量或者静态变量；

               .data段：初始化不为0的全局变量或者静态变量；

常量区：存放常量(比如比变量名字，非0的初始化值，const常量，字符串等)，只读；

代码区：存放代码的位置，只读；

 我们再来看这样的一串代码运行的结果：

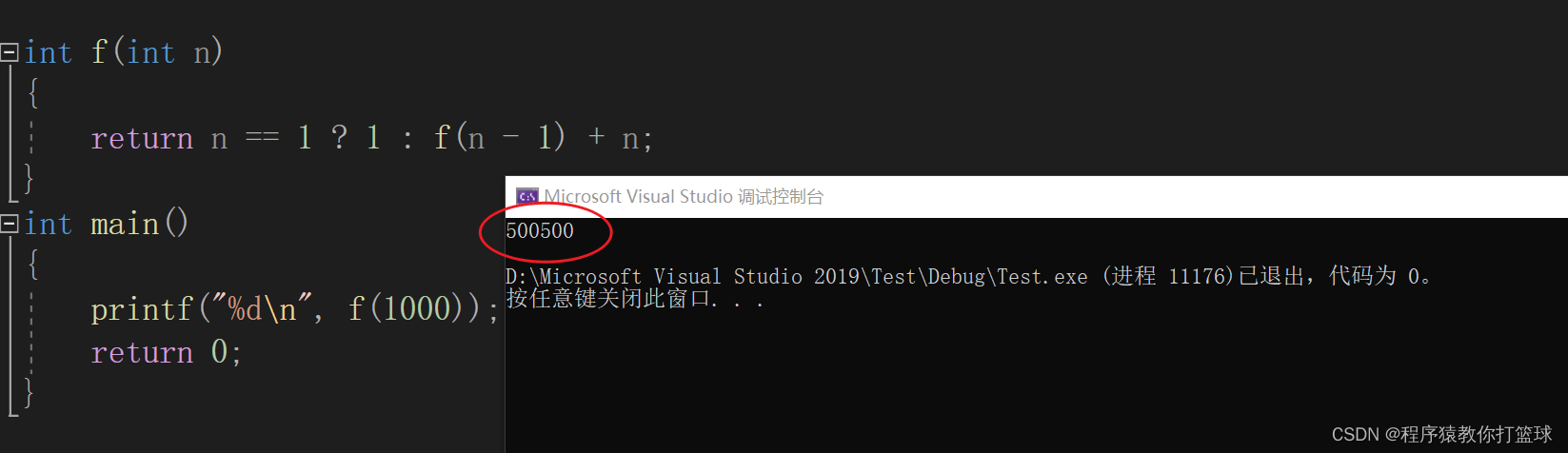
这是一个累加求和的递归函数，当我们发现累加求和到1000递归仍然能正常执行，我们接着改为10000看看是否还能正常运行？ 

我们可以看到，当数值达到10000的时候程序已经崩了，并不会显示任何错误，当我们进入调试可以发现报错显示栈溢出，那为什么会造成栈溢出呢，我们接着往下看！ 

 递归的基本认识：

 递归本质也是函数调用，是函数调用，本质就要形成和释放栈帧

 调用函数是有成本的，这个成本就体现在形成和释放栈帧上：时间+空间

 所以，递归就是不断形成栈帧的过程

内存和CPU的资源是有限的，也就决定了，合理的递归是绝对不能无限递归下去，如果递归调用深度太深，这样有可能导致一 直开辟栈空间，最终产生栈空间耗尽的情况，这样的现象我们称为栈溢出！

既然使用递归极端情况下会出现栈溢出的问题，那么我们就用非递归的方式来实现快速排序和归并排序！

2、快速排序（非递归实现）

快速排序非递归实现思想：

首先我们可以借助数据结构的栈来完成，遵循栈的后进先出，我们可以先入右再入左，然后使用我们上一期讲的三个方法中的其中一个方法，这里我们选择挖坑法，使用挖坑法我们可以看作成两个区间也就是: [left, keyIndex - 1] 和 [keyIndex + 1, right]，如果区间存在我们接着入栈，如此循环直到栈为空，则排序结束！

图解见下：

 代码实现如下：

//挖坑法 - 升序
int PartSort(int* a, int left, int right)
{
	int begin = left;
	int end = right;
	int key = a[begin];
	int pivot = begin;

	while (begin < end)
	{
		while (begin < end && a[end] >= key)
		{
			--end;
		}
		a[pivot] = a[end];
		pivot = end;

		while (begin < end && a[begin] <= key)
		{
			++begin;
		}
		a[pivot] = a[begin];
		pivot = begin;
	}

	pivot = begin;//当begin与end相遇，随便把begin和end的值给pivot
	a[pivot] = key;

	return pivot;
}

void QuickSortNonR(int* a, int n)
{
	Stack st;
	StackInit(&st);//初始化栈
	StackPush(&st, n - 1);//入数组最后一个元素下标
	StackPush(&st, 0);//入数组第一个元素下标

	while (!StackEmpty(&st))//当栈不为空我们就进入循环
	{
		int left = StackTop(&st);//取出栈顶元素给left
		StackPop(&st);//出栈 - 删除栈顶元素

		int right = StackTop(&st);
		StackPop(&st);

		int keyIndex =  PartSort(a, left, right);//使用挖坑法区间排序

		//[left, keyIndex - 1] keyIndex [keyIndex + 1, right]  -  分成子区间

		if (keyIndex + 1 < right)//因栈后进先出的特性，所以先入右区间
		{
			StackPush(&st, right);
			StackPush(&st, keyIndex + 1);
		}

		if (left < keyIndex - 1)
		{
			StackPush(&st, keyIndex - 1);
			StackPush(&st, left);
		}
	}

	StackDestory(&st);//销毁栈
}

3、归并排序（非递归实现）

归并排序非递归实现思想：

上期我们知道归并需要开辟一个数组，并且使用分治的算法来实现归并排序，而非递归版本我们的思路也是差不多，先让他们一个一个归并，然后两个两个归并，再接着四个四个一起归并，具体图解见下：

 代码实现如下：

void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc:");
		return;
	}

	int gap = 1;//gap为每组数据的个数，每次翻倍

	while (gap < n)
	{
		for (int i = 0; i < n; i += 2 * gap)
		{
			//可以看成 [i, i + gap - 1]  [i + gap, i + 2 * gap - 1]
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;

			//归并过程中右半区间有可能不存在！
			if (begin2 >= n)
				break;
			//归并过程中右半区间越界了，就修正下
			if (end2 >= n)
			{
				end2 = n - 1;
			}

			int index = i;
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] < a[begin2])
				{
					tmp[index++] = a[begin1++];
				}
				else
				{
					tmp[index++] = a[begin2++];
				}
			}

			while (begin1 <= end1)
			{
				tmp[index++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[index++] = a[begin2++];
			}

			//拷贝进去
			for (int j = i; j <= end2; ++j)
			{
				a[j] = tmp[j];
			}
 		}
		gap *= 2;
	}
	free(tmp);
}

本期到这里就结束了，相信你们已经对非递归快速排序和归并排序已经很了解了，非递归这两个在校招中经常会考，加油把！

gitee(码云)：Mercury. (zzwlwp) - Gitee.com       

到此这篇关于C语言非递归算法解决快速排序与归并排序产生的栈溢出的文章就介绍到这了,更多相关C语言 栈溢出内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！