C语言 链式二叉树结构详解原理

目录

• 前言
• 二叉树节点声明
• 二叉树的遍历
• 构建二叉树
• 1.前序遍历
• 2.中序遍历
• 3.后序遍历
• 二叉树节点的个数
• 二叉树叶子节点的个数
• 二叉树第K层节点个数
• 二叉树的高度/深度
• 二叉树查找值为x的节点
• 整体代码

前言

二叉树不同于顺序表，一颗普通的二叉树是没有增删改查的意义。普通的二叉树用来存储数据是不方便的。但是二叉树的一些基本实现结构，例如前序遍历，中序遍历。。。等等都是对我们学习更深层次的二叉树打下夯实的基础。

二叉树节点声明

typedef char BTDataType;

typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

二叉树的遍历

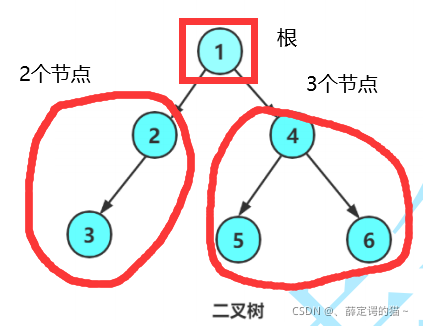
二叉树的遍历，是学习二叉树结构的重要部分。二叉树的遍历主要分为三种：1.前序遍历 2.中序遍历 3.后序遍历。首先我们要知道一颗二叉树分为根，左子树，右子树。而三种遍历方式也是围绕着根来实现的。

构建二叉树

我们按上图来构建一颗二叉树

BTNode* CreatTreeNode(BTDataType x)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTDataType));
	node->data = x;
	node->right = NULL;
	node->left = NULL;
	return node;
}
int main()
{
   	BTNode* A = CreatTreeNode('A');
	BTNode* B = CreatTreeNode('B');
	BTNode* C = CreatTreeNode('C');
	BTNode* D = CreatTreeNode('D');
	BTNode* E = CreatTreeNode('E');
	BTNode* F = CreatTreeNode('F');
	A->left = B;
	A->right = C;
	B->left = D;
	C->left = E;
	C->right = F;

}

1.前序遍历

前序遍历的顺序为 根 左子树 右子树 顾名思义就是先访问根节点再访问左节点最后访问右节点。

按照前序遍历，则上图的遍历顺序为：A B D NULL NULL NULL C E NULL NULL F NULL NULL

// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root)
{
	if (root == NULL) //等于NULL就直接返回
	{
		printf("NULL ");
		return;
	}
	printf("%c ", root->data);// 打印节点
	BinaryTreePrevOrder(root->left);//递归到左子树
	BinaryTreePrevOrder(root->right);//递归到右子树
}

2.中序遍历

中序遍历的顺序为 左子树 根 右 顾名思义就是先访问左节点再访问根节点最后访问右节点。

按照中序遍历，则上图的遍历顺序为：NULL D NULL B NULL A NULL E NULL C NULL F NULL

// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{
	if (root == NULL) //等于NULL就直接返回
	{
		printf("NULL ");
		return;
	}
	BinaryTreePrevOrder(root->left);//递归到左子树
	printf("%c ", root->data);//打印节点
	BinaryTreePrevOrder(root->right);//递归到右子树
}

3.后序遍历

后序遍历的顺序为 左子树 右子树 根 顾名思义就是先访问左节点，再访问右节点，最后访问根。

按照后序遍历，则上图的遍历顺序为：NULL NULL D NULL B NULL NULL E NULL NULL F C A

// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{
	if (root == NULL)//等于NULL直接返回
	{
		printf("NULL ");
		return;
	}
	BinaryTreePostOrder(root->left);//递归到左子树
	BinaryTreePostOrder(root->right);//递归到右子树
	printf("%c ", root->data);//打印节点

}

二叉树节点的个数

求二叉树节点的个数与上述遍历类似，都是通过递归函数来实现。一颗二叉树的节点个数主要以三个部分构成：根节点+左子树的节点个数+右子树的节点个数。知道这个公式我们就可以实现代码

// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{
	if (root == NULL)//如果为空返回零
	{
		return 0;
	}
	return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}

二叉树叶子节点的个数

叶子节点的左右子树都为空，知道这个，我们只需稍微改动上述代码即可

// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if ((root->left == NULL) && (root->right == NULL))
	{
		return 1;
	}

	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);

}

二叉树第K层节点个数

如果指定一颗二叉树，求它第K层节点个数，也可以采用递归的思想，当给定的K为零的时候此时就是求根节点的个数，显而易见就是返回1；而K不为零时，我们可以求root左右子树K-1层的节点数之和。

// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
	if (root == NULL)
	{
		return 0;
	}
	if (k == 1)
	{
		return 1;
	}
	return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}

二叉树的高度/深度

二叉树的高度就是指二叉树节点层次的最大值，也就是左右子树最大高度+1.

//二叉树深度/高度
int BinaryTreeDepth(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	int leftDepth = BinaryTreeDepth(root->left);
	int rightDepth = BinaryTreeDepth(root->right);

	return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
}

二叉树查找值为x的节点

// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)  //根为空，直接返回NULL
	{
		return NULL;
	}
	if (root->data == x)//找到了 直接返回节点
	{
		return root;
	}
	BTNode* leftRet = BinaryTreeFind(root->left, x);
	if (leftRet)
	{
		return leftRet; //如果再左子树找到，直接返回，无需递归到右子树

	}
	BTNode* rightRet = BinaryTreeFind(root->right, x);
	if (rightRet)
	{
		return rightRet; 

	}

	return NULL;  //如果都没找到，就直接返回NULL

}

整体代码

#pragma once
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
typedef char BTDataType;

typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

BTNode* CreatTreeNode(BTDataType x);
// 二叉树节点个数
int BinaryTreeSize(BTNode* root);
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root);
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root);
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root);
//二叉树深度/高度
int BinaryTreeDepth(BTNode* root);

#include"BinarryTree.h"

BTNode* CreatTreeNode(BTDataType x)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTDataType));
	assert(node);
	node->data = x;
	node->right = NULL;
	node->left = NULL;
	return node;
}

// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return ;
	}
	printf("%c ", root->data);
	BinaryTreePrevOrder(root->left);
	BinaryTreePrevOrder(root->right);
}

// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return ;
	}
	BinaryTreePrevOrder(root->left);
	printf("%c ", root->data);
	BinaryTreePrevOrder(root->right);
}

// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return ;
	}
	BinaryTreePostOrder(root->left);
	BinaryTreePostOrder(root->right);
	printf("%c ", root->data);

}

// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}

// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if ((root->left == NULL) && (root->right == NULL))
	{
		return 1;
	}

	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);

}

// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
	if (root == NULL)
	{
		return 0;
	}
	if (k == 1)
	{
		return 1;
	}
	return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}

// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
	{
		return NULL;
	}
	if (root->data == x)
	{
		return root;
	}
	BTNode* leftRet = BinaryTreeFind(root->left, x);
	if (leftRet)
	{
		return leftRet;

	}
	BTNode* rightRet = BinaryTreeFind(root->right, x);
	if (rightRet)
	{
		return rightRet;

	}

	return NULL;

}
// 二叉树销毁
void BinaryTreeDestory(BTNode** root)
{
	if (*root)
	{
		BinaryTreeDestory(&(*root)->left);
		BinaryTreeDestory(&(*root)->right);
		free(*root);
		*root = NULL;
	}
}

//二叉树深度/高度
int BinaryTreeDepth(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	int leftDepth = BinaryTreeDepth(root->left);
	int rightDepth = BinaryTreeDepth(root->right);

	return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
}

#include"BinarryTree.h"

int main()
{
	BTNode* A = CreatTreeNode('A');
	BTNode* B = CreatTreeNode('B');
	BTNode* C = CreatTreeNode('C');
	BTNode* D = CreatTreeNode('D');
	BTNode* E = CreatTreeNode('E');
	BTNode* F = CreatTreeNode('F');
	A->left = B;
	A->right = C;
	B->left = D;
	C->left = E;
	C->right = F;

	return 0;
}

到此这篇关于C语言 链式二叉树结构详解原理的文章就介绍到这了,更多相关C语言 链式二叉树结构内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！